Физический смысл потока
Закон Гаусса для электростатики
Векторное поле
Если каждой точке пространства поставлен в соответствие единственный вектор 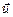 , то говорят, что задано векторное поле.
, то говорят, что задано векторное поле.
Примерами векторного поля могут служить поле скоростей частиц жидкости в трубе (рис. 4.1); поле вектора напряженности точечного заряда +q (рис. 4.2); поле вектора ускорения свободного падения вблизи поверхности Земли (однородное поле) (рис. 4.3).
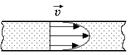
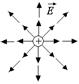
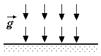
Рис. 4.1 Рис. 4.2 Рис. 4.3
 Пусть дано векторное поле
Пусть дано векторное поле 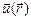 (здесь
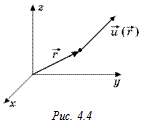
(здесь 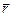 – радиус-вектор данной точки пространства) (рис. 4.4). Рассмотрим площадку DS, маленькую настолько, что в пределах ее вектор
– радиус-вектор данной точки пространства) (рис. 4.4). Рассмотрим площадку DS, маленькую настолько, что в пределах ее вектор 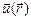 можно считать постоянным.
можно считать постоянным.
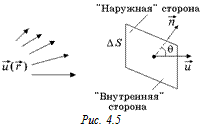 Для того чтобы определить, какая сторона у площадки «внутренняя», а какая «наружная», удобно ввести вспомогательный единичный вектор
Для того чтобы определить, какая сторона у площадки «внутренняя», а какая «наружная», удобно ввести вспомогательный единичный вектор 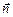 , который перпендикулярен к площадке и указывает «наружу». Этот вектор называют нормалью к площадке (рис. 4.5).
, который перпендикулярен к площадке и указывает «наружу». Этот вектор называют нормалью к площадке (рис. 4.5).
Потоком векторного поля 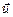 через площадку DS, имеющую нормаль
через площадку DS, имеющую нормаль 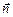 , называется величина
, называется величина
Ф = | 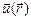 |×DS cosq, (1)
|×DS cosq, (1)
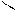
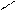
где q = 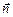 ,
, 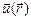 – угол между векторами
– угол между векторами 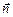 и
и 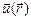 .
.
Выражение (1) можно также представить в виде
Ф = ( 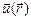 ,
, 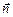 )×DS,
)×DS,
где ( 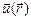 ,
, 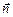 ) – скалярное произведение векторов
) – скалярное произведение векторов 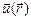 и
и 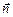 .
.
Задача 4.1. Напряженность однородного электрического поля равна  . Чему равен поток векторного поля напряженности (или просто поток напряженности) через квадрат со стороной l, плоскость которого расположена под углом a = 30° к направлению поля. Направление нормали указано на рис. 4.6.
. Чему равен поток векторного поля напряженности (или просто поток напряженности) через квадрат со стороной l, плоскость которого расположена под углом a = 30° к направлению поля. Направление нормали указано на рис. 4.6.
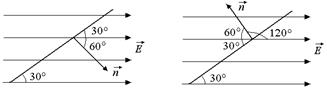
а б
Рис. 4.6
Решение.
а) 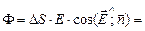
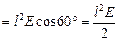 ; ;
| б) 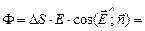
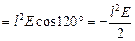 . .
|
Ответ: а) Ф = 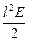 ; б) Ф = –
; б) Ф = – 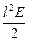 .
.
Физический смысл потока
Векторного поля
Пример. Введем векторное поле 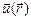 , у которого модуль
, у которого модуль 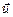 в точке
в точке 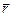 есть число дробинок, пересекающих за единицу времени единичную площадку, перпендикулярную вектору
есть число дробинок, пересекающих за единицу времени единичную площадку, перпендикулярную вектору 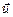 , а направление
, а направление 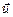 совпадает с направлением скорости дробинок в данной точке (рис. 4.7).
совпадает с направлением скорости дробинок в данной точке (рис. 4.7).
Покажем, что в данном случае поток вектора 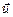 через площадку DS – это число дробинок, пересекающих площадку в направлении нормали в единицу времени.
через площадку DS – это число дробинок, пересекающих площадку в направлении нормали в единицу времени.
 Случай 4 Случай 4
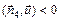
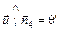
 90° < q¢ < 180°
Случай 2 90° < q¢ < 180°
Случай 2
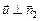
|   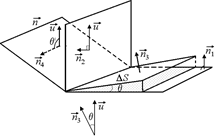
| Случай 3
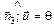 0° < q < 90°
DSx = DScosq
Случай 1
0° < q < 90°
DSx = DScosq
Случай 1
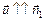
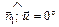
|
Рис. 4.7
1. Пусть 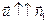 (случай 1 на рис. 4.7), тогда через площадку DS пройдет за единицу времени
(случай 1 на рис. 4.7), тогда через площадку DS пройдет за единицу времени
| 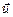 |DS = |
|DS = | 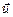 |DSсоs0° = (
|DSсоs0° = ( 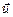 ,
, 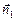 )DS = Ф (дробинок).
)DS = Ф (дробинок).
2. Пусть 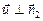 (случай 2 на рис. 4.7), тогда через площадку DS вообще не пройдет ни одна дробинка, т.е. пройдет ноль дробинок:
(случай 2 на рис. 4.7), тогда через площадку DS вообще не пройдет ни одна дробинка, т.е. пройдет ноль дробинок:
0 = | 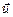 |DSсоs90° = (
|DSсоs90° = ( 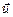 ,
, 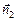 )DS = Ф.
)DS = Ф.
3. Пусть 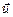 составляет с нормалью угол q (случай 3 на рис. 4.7), тогда число дробинок, пересекающих площадку DS в единицу времени, будет равно произведению |
составляет с нормалью угол q (случай 3 на рис. 4.7), тогда число дробинок, пересекающих площадку DS в единицу времени, будет равно произведению | 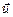 | на площадь проекции DSх площадки DS на плоскость, перпендикулярную вектору
| на площадь проекции DSх площадки DS на плоскость, перпендикулярную вектору 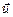 , т.е.
, т.е.
| 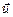 |DSх = |
|DSх = | 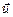 |(DScosq) = (
|(DScosq) = ( 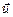 ,
, 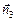 )DS = Ф.
)DS = Ф.
Следовательно, поток вектора 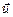 через площадку DS – это число дробинок, пересекающих эту площадку за единицу времени в направлении нормали
через площадку DS – это число дробинок, пересекающих эту площадку за единицу времени в направлении нормали 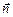 .
.
Заметим, что если Ф < 0 (случай 4 на рис. 4.7), то это означает, что дробинки пересекают площадку в направлении, противоположном нормали 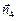 .
.
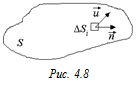 Рассмотрим произвольную поверхность S. Разобьем ее на элементарные площадки DSi, такие, чтобы в пределах каждой из них вектор
Рассмотрим произвольную поверхность S. Разобьем ее на элементарные площадки DSi, такие, чтобы в пределах каждой из них вектор 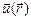 менялся незначительно (рис. 4.8).
менялся незначительно (рис. 4.8).
Потоком векторного поля 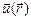 через произвольную поверхность S называется сумма потоков через каждую элементарную площадку, на которые разбита поверхность S, при устремлении площади каждой площадки DSi к нулю.
через произвольную поверхность S называется сумма потоков через каждую элементарную площадку, на которые разбита поверхность S, при устремлении площади каждой площадки DSi к нулю.
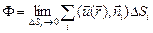 ,
,
где 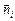 – нормаль к DSi, а символ lim (limit) означает «предел».
– нормаль к DSi, а символ lim (limit) означает «предел».
Для удобства записи вводят следующие обозначения:
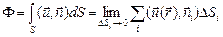 ,
,
где символ 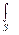 называется интегралом по поверхности S.
называется интегралом по поверхности S.
Пусть поверхность S замкнутая и нормаль 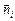 всегда направлена наружу, тогда поток через поверхность S есть полное число дробинок, вылетающих наружу из объема, ограниченного поверхностью S, за единицу времени.
всегда направлена наружу, тогда поток через поверхность S есть полное число дробинок, вылетающих наружу из объема, ограниченного поверхностью S, за единицу времени.
Заметим, что если Ф > 0, то это означает, что дробинок вылетает больше, чем влетает, т.е. внутри находится источник дробинок – ружье. Если Ф = 0 – дробинок вылетает и влетает поровну. Если Ф < 0, то дробинок влетает больше, чем вылетает, т.е. внутри находится поглотитель дробинок – мишень.
Задача 4.2. Вычислить поток вектора напряженности электрического поля точечного заряда +q через замкнутую поверхность S, имеющую форму узкой усеченной пирамиды (рис. 4.9). Основания пирамиды считать квадратами со сторонами а и b (а << ra, b << rb); 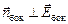 ;
; 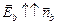 ;
; 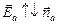 .
.
Рис. 4.9 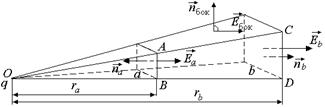
Решение. ФS = Фа + Фb + Фбок. Поскольку 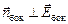 , то поток через боковые грани равен нулю.
, то поток через боковые грани равен нулю.
Фа = 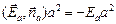 , так как
, так как 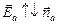 ;
;
Фb = 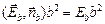 , так как
, так как 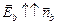 ;
;
Еа = 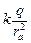 ; Еb =
; Еb = 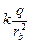 ;
;
ФS = Фа + Фb = –Еаа2 + Еbb2 = – 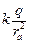 а2 +
а2 + 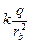 b2 =
b2 = 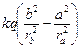 .
.
Поскольку DОАВ ∾DОCD , то 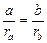 . Отсюда
. Отсюда
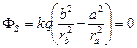 .
.
Ответ: ФS = 0.
Задача 4.3. Изменится ли результат задачи 4.2, если нормали 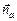 и
и 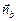 будут не параллельны вектору
будут не параллельны вектору  , т.е. если основания пирамиды будут как бы перекошены?
, т.е. если основания пирамиды будут как бы перекошены?
Решение. Ограничимся случаем, когда перекошено только нижнее основание (рис. 4.10).
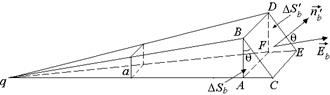 Рис. 4.10
Рис. 4.10
Как видно из DАВС, ВС = АВ/cosq, а значит, площадь «перекошенного» основания BDEC равна
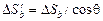 ,
,
где DSb – площадь старого основания ABDF. Тогда поток через «перекошенное» основание составит
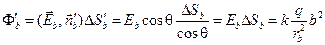 ,
,
т.е. поток через нижнее основание не изменится: 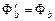 , следовательно, не изменится и полный поток.
, следовательно, не изменится и полный поток.
Ответ: ФS = 0.
Задача 4.4. Вычислить поток напряженности электростатического поля точечного заряда через произвольную замкнутую поверхность S для случая, когда заряд находится снаружи.
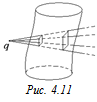 Решение. Объем, ограниченный поверхностью S, можно представить себе состоящим из большого числа очень узких усеченных пирамид с «перекошенными» основаниями, вплотную прилегающих друг к другу, а поверхность S – это совокупность верхних и нижних «оснований» этих пирамид (рис. 4.11). Поэтому ФS = 0.
Решение. Объем, ограниченный поверхностью S, можно представить себе состоящим из большого числа очень узких усеченных пирамид с «перекошенными» основаниями, вплотную прилегающих друг к другу, а поверхность S – это совокупность верхних и нижних «оснований» этих пирамид (рис. 4.11). Поэтому ФS = 0.
Задача 4.5. Замкнутая поверхность S1 целиком находится внутри замкнутой поверхности S2. Точечный заряд находится внутри поверхности S1 (рис. 4.12,а). Доказать, что поток вектора напряженности электрического поля заряда q через поверхность S1 равен потоку через поверхность S2: 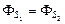 .
.
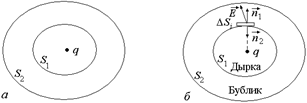
Рис. 4.12
Доказательство. Условно назовем объем, находящийся внутри поверхности S1, «дыркой», а объем, заключенный между поверхностями S1 и S2 – «бубликом» (рис. 4.12,б).
1. Покажем, что поток напряженности электрического поля, «вытекающий» из «дырки» через поверхность S1, равен потоку, «вытекающему» из «бублика» через поверхность S1, взятому со знаком минус.
Разобьем поверхность S1 на малые площадки DSi 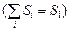 . Рассмотрим площадку DSi на поверхности S1. Пусть
. Рассмотрим площадку DSi на поверхности S1. Пусть 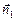 – нормаль к площадке DSi, направленная наружу из «дырки», а
– нормаль к площадке DSi, направленная наружу из «дырки», а 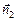 – нормаль к площадке DSi, направленная наружу из «бублика». Очевидно, что
– нормаль к площадке DSi, направленная наружу из «бублика». Очевидно, что 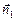 = –
= – 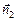 .
.
Поток, «вытекающий» из «дырки» через DSi, равен
DФдырки = 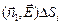 ,
,
а поток, «вытекающий» из «бублика» через DSi, равен
DФбублика = 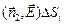 = –
= – 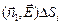 ,
,
где  – напряженность электрического поля в том месте, где находится площадка DSi. Как видим, DФдырки = –DФбублика.
– напряженность электрического поля в том месте, где находится площадка DSi. Как видим, DФдырки = –DФбублика.
Поскольку последнее равенство справедливо для произвольной площадки DSi, то, суммируя по всем малым площадкам, получим
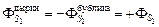 .
.
2. Поток через поверхность, ограничивающую «бублик» со всех сторон, равен нулю, так как поверхность бублика – это замкнутая поверхность, не содержащая заряда. Тогда
Фбублика = 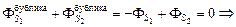
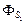 =
= 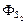 и т.д.
и т.д.
Задача 4.6. Внутри произвольной замкнутой поверхности S находится точечный заряд q > 0 (рис 4.13). Определить поток вектора напряженности  через эту поверхность.
через эту поверхность.
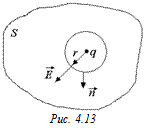 Решение. Окружим заряд q сферой радиуса r, целиком лежащей внутри поверхности S. Согласно решению задачи 4.5 поток через поверхность S равен потоку через сферу. Учитывая, что в каждой точке сферы напряженность
Решение. Окружим заряд q сферой радиуса r, целиком лежащей внутри поверхности S. Согласно решению задачи 4.5 поток через поверхность S равен потоку через сферу. Учитывая, что в каждой точке сферы напряженность 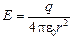 и направлена вдоль радиуса, а площадь поверхности сферы S = = 4pr2, получим
и направлена вдоль радиуса, а площадь поверхности сферы S = = 4pr2, получим
ФS = (поток из сферы) = E(r)(4pr2) =
= 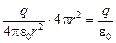 .
.
Ответ: 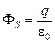 .
.
(Вот где оказался удобным коэффициент 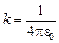 !)
!)
Заметим, что если заряд q – отрицательный, то 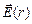 направлена у центру сферы
направлена у центру сферы 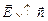 и
и 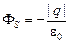 , но если учесть, что q < 0, то можно записать
, но если учесть, что q < 0, то можно записать 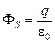 .
.
Вывод: поток напряженности поля точечного заряда q через любую замкнутую поверхность S равен:
1) нулю, если заряд расположен снаружи;
2) q/e0, если заряд расположен внутри, где заряд q берется с учетом знака.
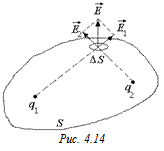
Задача 4.7. Определить поток напряженности поля, созданного двумя точечными зарядами q1 и q2, через произвольную замкнутую поверхность S (рис. 4.14).
Решение. Рассмотрим поток DФ вектора  через малую площадку DS:
через малую площадку DS:
DФ = (  ,
, 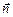 )DS =
)DS = 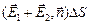 =
=
= 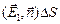 +
+ 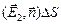 = DФ1 + DФ2,
= DФ1 + DФ2,
 где DФ1 и DФ2 – потоки напряженности поля соответственно зарядов q1 и q2 через площадку DS. Поскольку всю поверхность S можно представить как совокупность малых площадок DSi, то
где DФ1 и DФ2 – потоки напряженности поля соответственно зарядов q1 и q2 через площадку DS. Поскольку всю поверхность S можно представить как совокупность малых площадок DSi, то
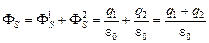 .
.
Ответ: 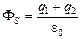 .
.
Заметим, что если один из зарядов находится снаружи, то поток напряженности поля, созданного этим зарядом, равен нулю.
Для произвольного числа зарядов справедлив закон Гаусса:
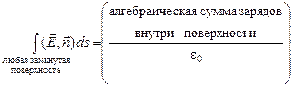
Дата добавления: 2016-04-11; просмотров: 4327;
