Представление синусоидальных величин вращающимися векторами и комплексными числами
· Представление синусоидальных функций вращающимися векторами
Расчет переменных токов и напряжений с помощью алгебраических операций их мгновенных значений по исходным выражениям (1.1а) − (1.1в) весьма неудобен из-за громоздких вычислений. Графическое представление синусоидальных величин (см. рис.1.3) достаточно наглядно для одной, двух синусоид, но для сложных цепей практически не используется, ввиду трудности построения и анализа нескольких синусоидальных величин.
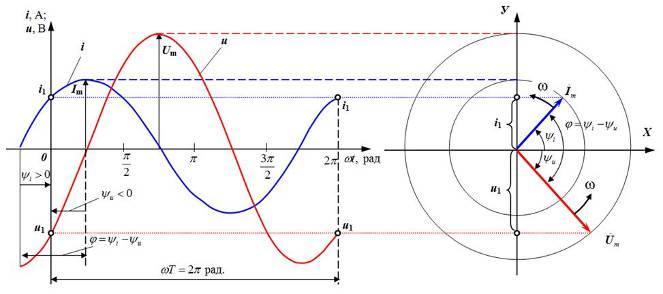
Представления синусоидальных функций при помощи вращающихся векторов (векторных диаграмм), как показано на рис 1.4, позволяет наглядно показать количественные и фазовые соотношения между разными напряжениями, токами и широко используется при объяснении процессов в цепях переменного тока.
Мгновенное значение синусоидальной функции времени t или угла поворота wtможно представить в виде изменяющейся проекции на вертикальную ось вращающегося с угловой скоростью wвектора, как показано на рис 1.4. Векторы, изображающие синусоидальные функции времени, обозначаются, как и комплексные величины, точками вверху. Сравнивая рисунки 1.4,а и 1.4,б, можно видеть что длины векторов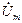 
и 
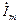равны амплитудам напряжения Um и тока Im синусоидальных функций напряжения uи тока i.
а) б)
Рис.1.4. Соответствие синусоидальных функций u, i
и вращающихся векторов 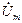и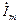
а) – графики мгновенных значений синусоидальных величин напряжения и тока; б)–вращающиеся с угловой скоростью ω векторы 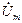и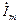
Проекции вращающихся с угловой скоростью ω векторов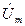 
и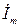 
на ось ординат У (рис. 1.4,б) равны мгновенным значениям синусоидальных функций напряжения uи тока i (рис. 1.4,а)
u = Umsin(wt – yu) ; i = Imsin(wt + yi). (1.4)
Углы наклона к оси абсцисс Х векторов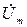 
и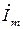 
изменяются с угловой скоростью wи для момента времени t = t1 соответствуют фазам yu1 и yi1, поскольку для этого момента:
yu1 = wt1 – yu ; yi1 = wt1+ yi.
Начальные фазы yu и yi будут соответствовать углам наклона векторов 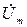и 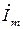к оси Хв начальный момент времени t = 0 (рис. 1.4,б). Легко убедится, что векторы 
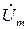и 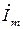, вращающиеся с одной угловой скоростью w, будут взаимно неподвижнымии для любого момента времени сохраняют неизменным сдвиг фаз между напряжением и током:
j = yi – yu = const.
Так как фазовые сдвиги между напряжениями, токами и ЭДС одной частоты w остаются неизменными в течение времени, то от системы вращающихся векторов можно перейти к эквивалентной системе неподвижных векторов для момента времени t = 0.
В электротехнике принято оперировать действующими значениями величин напряжений U , ЭДС Е и токов I. Поэтому длины векторов на векторных диаграммах соответствуют не амплитудным, а действующим значениям, которые, как было выше сказано в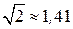 
раз меньше амплитудных значений.
Углы наклона векторов напряжения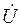 
и тока 
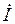к оси абсцисс (рис. 1.4,б) равны начальным фазам yu и yi (см. рис. 1.4,а). Таким образом, неподвижные векторы определяют два параметра синусоидальной величины: действующее значение и начальную фазу. Третий параметр – угловая частота w должен быть заранее известен.
За положительное направление вращения векторов с угловой скоростьюw принято направление вращения против часовой стрелки (см. рис 1.4,б). Первый по вращению вектор считается опережающим следующий за ним вектор нафазовый угол j, который, в свою очередь, считается отстающим на тот же угол j относительно первого вектора. Например, на рис. 1.4,а вектор напряжения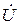 
опережает вектор тока 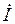на фазовый угол j или наоборот, можно считать, что вектор тока 
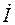отстает относительно вектора 
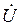на тот же угол j.
Если для синусоидальных величин одной частоты начальные фазы одинаковы, то векторы этих величин направлены в одну сторону, фазовый угол между ними равен нулю (j=0) и говорят, что эти величины совпадают по фазе (синфазны). Когда для синусоидальных величин разность фаз j = ±p, то векторы этих величин направлены в противоположные стороны и говорят, что эти величины противоположны по фазеили находятся в противофазе.
Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, относящиеся к одной цепи, называют векторной диаграммой.
Применение векторных диаграмм делает наглядным анализ электрический цепи. В этом методе сложение и вычитание мгновенных значений синусоидальных величин можно заменить геометрическим сложением и вычитанием их векторов, по правилам, представленным в Приложении 4.
· Представление синусоидальных функций комплексными числами
Применение векторных диаграмм для анализа цепей переменного тока, несмотря на простоту и наглядность, не всегда дает достаточную точность при расчетах. Метод представления синусоидальных функций комплексными величинами и оперирование с ними как с комплексными числами, называемый комплексным методом [1], объединяет в себе простоту векторных диаграмм с возможностью производить расчеты с любой заданной степенью точности.
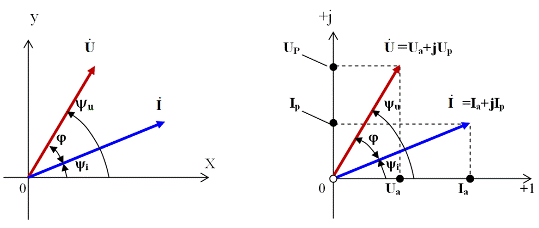
Комплексный метод основан на представлении векторов из декартовой системы координат (рис. 1.5,а) в комплексной плоскости (см. рис. 1.5,б) и на записи их комплексными числами. Это позволяет для цепей синусоидального тока применять законы Ома и Кирхгофа и методы расчета этих цепей в той же форме, что и для цепей постоянного тока, конечно с учетом специфики оперирования с комплексными величинами.
а) б)
Рис. 1.5. Соответствие векторов и комплексных чисел
а) – векторы действующих значений тока I и напряжения U на векторной диаграмме;
б) – представление векторов тока и напряжения на комплексной плоскости
Синусоидальную функцию тока или напряжения можно однозначно изобразить соответствующим вектором в декартовых координатах (см. рис. 1.5,а) или на комплексной плоскости (рис. 1.5,б). В свою очередь, каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое можно записать в алгебраической, тригонометрической или показательной форме. Например, комплексы тока 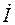инапряжения 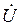на рис. 1.5,б, соответствующие векторам тока 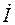и напряжения 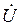на векторной диаграмме рис. 1.5,а, можно представить в алгебраической форме:
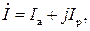
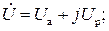
в тригонометрической форме:
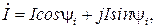
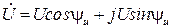
и показательной форме:
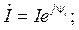
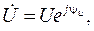
где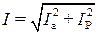 
и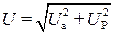 
– модули комплексов тока и напряжения, равные длинам векторов этих величин, которые определяют действующие значения соответствующего тока и напряжения;
yi = arctgIр/Iа и yu = arctgUр/Uа – аргументы комплексовтока и напряжения, равные их начальным фазам;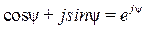 
– формула Эйлера, связывающая алгебраическую и показательную формы записи комплексных чисел; е – основание натурального логорифма; 
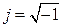– мнимая единица.
Примечание В электротехнике мнимая единица обозначается буквой j, в отличие от математики, где мнимая единица – i(а в электротехнике i– это принятое обозначение тока).
Таким образом, комплексное число или просто комплекс тока или напряжения в любой из выше перечисленных форм записи является отображением соответствующей синусоидальной функции тока или напряжения.
· Правила операций с векторами и комплексными величинами
Если исходный вектор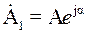 
повернуть на комплексной плоскости из положения 1 в положение 2 против часовой стрелки на угол β (см. рис. 1.6), то в комплексной форме это запишется как 
.
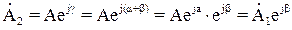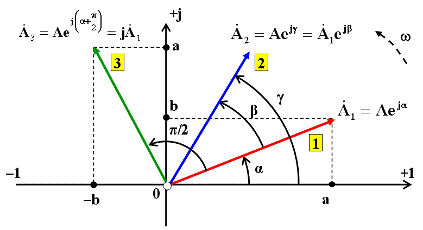
Рис. 1.6. Операция поворота вектора на комплексной плоскости
Следовательно, умножение комплексного числа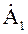 
на множитель типа 
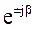соответствует повороту вектора 
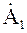на комплексной плоскости на угол ±b, причем угол +b откладывается против часовой стрелки, а (-b) – по ходу часовой стрелки.
Если угол b = p/2= 90°, то из формулы Эйлера следует:
.
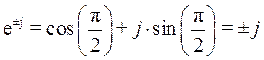То есть умножение комплексного числа на мнимую единицу ±j соответствует повороту вектора на комплексной плоскости на угол ±p/2.
Если взять, например, комплекс в алгебраической форме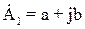 
, изображенный вектором 
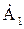в положении 1 (см. рис. 1.6), то, умножив его +j, получим 
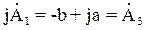, что при его графическом построении на комплексной плоскости соответствует повороту исходного вектора 
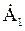на угол p/2 в положительном направлении (против часовой стрелки) из положения 1 в положение 3.
Считая угол поворотного множителя функцией времени, когда b = wt, получаем множитель или оператор вращения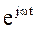 
. В этом случае вектор станет радиусом-вектором, вращающимся относительно начала координат на комплексной плоскости с угловой скоростью w против часовой стрелки, что записывается в виде: 
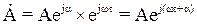. Это выражение называют комплексной функцией времени или комплексным мгновенным значением.
Комплексное число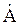 
будетдействительным числом А, когда сомножитель b при мнимой единице будет равен нулю, при этом аргумент комплексного числа – угол α будет равен нулю или π, а на комплексной плоскости этому действительному числу будет соответствовать вектор проведенной вдоль оси действительных чисел вправо от нуля (при угле α = 0)или влево от нуля (отрицательные числа при угле α = π).Комплексное число 
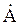называется мнимым, когда действительное число а = 0, а аргумент комплексного числа – угол α будет равен ±π/2. На комплексной плоскости этому мнимому числу будет соответствовать вектор проведенной вдоль вертикальной оси мнимых чисел ±j.
Операции сложения, вычитания, умножения и деления синусоидальных функций времени производят путем тех же алгебраических действий с соответствующими комплексными числами или векторами на комплексной плоскости. Переход от алгебраической формы записи комплексного числа к показательной форме, и наоборот, соответствует переходу от декартовых координат к полярным и от полярных координат – к декартовым. При этом операции алгебраического сложения и вычитания комплексных чисел, записанных в алгебраической форме, заменяются эквивалентными операциями геометрического сложения и вычитания соответствующих комплекс-векторов, записанных в показательной форме. Выбор той или иной формы записи комплексных чисел определяется простотой и удобством оперирования для определенной математической операции. Так, при сложении и вычитании комплексных чисел более удобна алгебраическая форма записи, а при умножении и делении – показательная.
Дата добавления: 2016-04-11; просмотров: 10476;