Принцип строгой индукции. Пусть S(n) – некоторое высказывание о целом числе n и требуется доказать, что S(n) справедливо для всех положительных n

Пусть S(n) – некоторое высказывание о целом числе n и требуется доказать, что S(n) справедливо для всех положительных n. Для этого необходимо:

1) доказать, что справедливо S(1);

2) доказать, что если справедливы S(1), S(2), S(3), ..., S(n) для всех положительных n, то справедливо и S(n + 1).

Отметим, что эта версия индукции почти идентична простой индукции, за одним исключением: при доказательстве второго положения в качестве гипотезы предполагается не просто справедливость высказывания S(n), а справедливость высказываний S(1), S(2), S(3), ..., S(n). Исходя из этой более строгой гипотезы, необходимо, как и выше, доказать справедливость S(n + 1).

Интуитивно ясно, что эти два положения подразумевают справедливость S(n) для любого положительного числа n. Из первого положения известно, что S(1) справедливо, а из второго следует, что если справедливо S(1), то справедливо и S(2). Так как S(1) действительно справедливо, следовательно, то же можно сказать и о S(2). Затем, так как и S(1), и S(2) справедливы, из второго положения следует справедливость S(3). Из справедливости высказываний S(1), S(2), S(3) и второго утверждения вытекает справедливость высказывания S(4) и т. д.

Рассмотрим несколько примеров, в которых полезно использовать принцип строгой индукции.

Пример 1.3. Простым числом называется положительное число, делящееся без остатка только на 1 и на само себя. Мы хотим доказать, что каждое положительное число n можно представить в виде произведения одного и более простых чисел. Докажем это с помощью строгой индукции по n:

1) если n = 1, то это число является простым, и, следовательно, его можно представить как «произведение» одного простого числа;

2) предположим, что каждое из чисел 1, 2, ..., n может быть записано в виде произведения простых чисел. Необходимо показать, что число n + 1 также можно представить в виде произведения простых чисел. Если n + 1 является простым числом, то очевидно, что его можно записать в виде произведения одного простого числа на 1. Если n + 1 – не простое число, тогда существует некоторое положительное число a, такое, что 1 < a < n + 1, и оно делит n + 1 без остатка.

Другими словами, 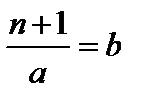, или n + 1 = a×b.

Каждое из чисел a и b меньше n. Следовательно, по гипотезе индукции и a, и b можно представить в виде произведения простых чисел. Отсюда очевидно, что и n + 1 можно записать как произведение этих же простых чисел, так как n + 1 = a×b.

Следует отметить, что в этом примере, по существу, требуется строгая индукция. О числах a и b известно лишь только то, что они меньше n. Поэтому, для того чтобы использовать индукцию, необходимо знать, что каждое из положительных чисел 1, 2, ... , n может быть представлено в виде произведения простых чисел. Одного предположения о том, что n можно записать в виде произведения простых чисел, оказывается недостаточно.

Пример 1.4. Рассмотрим последовательность чисел, называемых числами Фибоначчи. В нее входят f₀ = 0, f₁ = 1, f₂ = 1, f₃ = 2, f₄ = 3, f₅ = 5, f₆ = 8, ... , где (n + 1)-е число Фибоначчи определяется как f_{n + 1}= f_n + f_{n – 1} (для n ³ 1). Пусть = (1 + 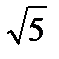)/2 и требуется доказать, что f_n £ a^{n – 1} для любого неотрицательного числа a. Для доказательства используем метод строгой индукции по n. Так как доказывается высказывание о неотрицательных числах, а принцип индукции сформулирован для положительных, используем модификацию метода:

1. Для n = 0 необходимо показать, что f₀ £ a^{0 – 1} . Это справедливо, так как f₀ = 0 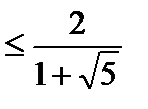= a^–1. Необходимо рассмотреть особый случай, когда n = 1. Здесь мы имеем f₁ = 1 £ 1=a⁰ = a^1–1.

2. Предположим, что f_m £ a^{m – 1} справедливо для всех неотрицательных целых чисел m = 0, 1, 2, ... , n. Нужно показать, что f_n+1 £ a^{(n + 1) – 1} также справедливо. По гипотезе индукции f_n £ a^{n – 1} и f_n–1 £ a^{(n – 1) – 1}. Поэтому

f_{n + 1} = f_n + f_{n – 1} £a^{n – 1} + a^{n – 2} = a^{n – 2} × (a+1).

Обратите внимание, что

a² 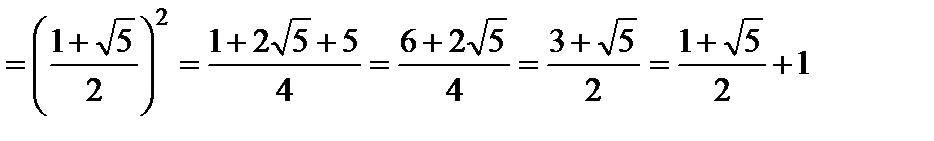= a + 1.

Фактически мы так и выбирали a, чтобы выполнялось условие a + 1 = a². Поэтому мы получаем

f_{n + 1} = f_n + f_{n – 1} £ a^{n – 2} × (a+1) = a^{n – 2} × a² = aⁿ = a^{(n + 1) – 1} .

что и требовалось доказать.

Отметим, что необходимо было знать, что и f_n, и f_n–1 удовлетворяют гипотезе индукции. Только в этом случае доказательство возможно. Одного только знания о справедливости высказывания для f_n недостаточно. Таким образом, строгая индукция нам необходима по существу. Отметим также, что в данном частном случае нам потребовалось доказывать, что f₀ £ a⁰ и f₁ £ a¹; мы не можем записать f₁ как f₀ + f_–1 , так как f_–1 не существует.

В качестве упражнения по данной теме попробуйте изменить приведенный в данном разделе принцип индукции для доказательства справедливости высказывания S(n) для целых чисел n, удовлетворяющих условию n ³ n₀, а не только для любых положительных целых чисел.