Описание метода индуктивных утверждений

Для доказательства частичной правильности (по отношению к А и С) программы (блок-схемы) поступим следующим образом. Свяжем утверждение А с началом программы, а утверждение С с конечной точкой программы. Кроме этого, выявим некоторые закономерности, относящиеся к значениям переменных, и свяжем соответствующие утверждения с другими точками программы. В частности, свяжем такие утверждения по крайней мере с одной из точек в каждом из замкнутых путей в программе (в циклах). Для каждого пути в программе, ведущего из точки I, связанной с утверждением А_I, в точку J, связанную с утверждением a_J (при условии, что на этом пути нет точек с какими-либо дополнительными утверждениями), докажем, что если мы попали в точку I и справедливо утверждение А_I, а затем прошли от точки I до точки J, то при попадании в точку J будет справедливо утверждение a_J. Для циклов точки I и J могут быть одной и той же точкой.

Чтобы убедиться, что таким способом мы действительно доказываем частичную правильность программы, докажем следующую теорему.

Теорема 1. Если можно выполнить все действия, предусмотренные описанным методом индуктивных утверждений для некоторой программы, то эта программа частично правильна (относительно А и С).

Доказательство. Предположим, что мы выполнили доказа­тельство правильности методом индуктивных утверждений. Начнем выполнять программу с начальными данными, удовлетворяющими допущению А. Нам нужно доказать, что если выполнение программы закончится, то утверждение С будет справедливо, но фактически мы докажем нечто более общее. Мы покажем, что каждый раз, когда мы попадаем в некоторую точку программы, с которой связано определен­ное утверждение, данное утверждение будет справедливым. Это, в частности, предполагает, что, если мы достигнем , последней точки программы (т. е. программа закончится), утверждение С будет справедливо. Доказательство проведем с помощью индукции по N –числу точек программы, через которые мы уже прошли (учитываются точки, связанные с некоторыми утверждениями).

1. Предположим, что в процессе выполнения программы мы попали в первую из этих точек (N = 1). Нужно показать, что связанное с этой точкой утверждение справедливо. Но первая точка – это начальная точка программы, и с ней связано исходное допущение А. Мы знаем, что оно справедливо, ибо речь идет о выполнении программы с такими начальными данными, для которых оно выполняется.

2. Предположим, что мы дошли до некоторой точки (N-й), с которой связано утверждение 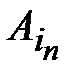. Допустим, что это утверждение справедливо (гипотеза индукции). Нужно пока­зать, что если выполнение продолжается и мы попадаем из N-й точки в (N+1)-ю, то связанное с ней утверждение 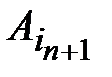будет также верным. Очевидно, что между N-й и (N+1)-й точками существует некоторый путь. Так как речь идет о методе индуктивных утверждений, то, следовательно, мы уже рассматривали этот путь и показали, что если находимся в N-й точке со справедливым утверждением 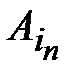, а затем проходим из N-й в (N+1)-ю точку, то при ее достижении будет справедливо утверждение 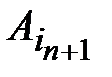. Из этого факта вместе с гипотезой о справедливости утверждения 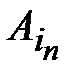следует, что при попадании в (N+1)-ю точку справедливо утверждение ,
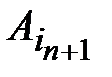т. е. то, что требовалось доказать.

Таким образом, мы доказали по индукции, что если программа удовлетворяет условиям метода индуктивных утверждений, то при достижении любой из точек программы, с которыми связаны определенные утверждения, соответст­вующие утверждения будут справедливы. Следовательно, если будет достигнута конечная точка программы, то будет справедливо утверждение о правильности, связанное с этой точкой, т. е. рассматриваемая программа является частично правильной.

Для доказательства полной правильности программы сначала методом индуктивных утверждений нужно доказать ее частичную правильность, а затем уже доказать, что программа когда-нибудь завершится. Проиллюстрируем этот прием на нескольких примерах программ, содержащих вложенные циклы. Студенту рекомендуется самому попытаться доказать правильность одной из этих программ с помощью использованного выше ограниченного метода, для того чтобы лучше оценить эффективность более общего метода.

Пример 2.4. Требуется доказать, что приведенная на рис. 7 блок-схема устанавливает переменную XLGST равной максимальному значению в массиве X. Указанные на блок-схеме утверждения – индуктивные утверждения, необходимые для доказательства частичной правильности программы. Так как все эти утверждения имеют аналогичную форму и начинаются с фразы: «При достижении этой точки справедливо…», то это начало фразы мы опускаем. Утверждение о конечности программы мы не помещаем на блок-схеме, поскольку доказательство этого утверждения проводится отдельно от доказательства частичной правильности.

Для доказательства частичной правильности нужно исследовать все пути программы. Рассмотрим их по порядку.

1. Путь из точки 1 в точку 2. Предположим, что мы находимся в точке 1 и связанное с ней утверждение справедливо, т. е. данные удовлетворяют исходному допущению. Перейдем из точки 1 в точку 2. Нужно показать, что после прихода в точку 2 связанное с этой точкой утверждение будет справедливо. Если мы попали в точку 2 из точки 1, то имеем I= 1 и XLGST = X_1,1. Так как M³1, то очевидно, что 1 £ I=1 £ M+1. Поскольку XLGST = X_1,1 и I=1, то утверждение о XLGST справедливо.

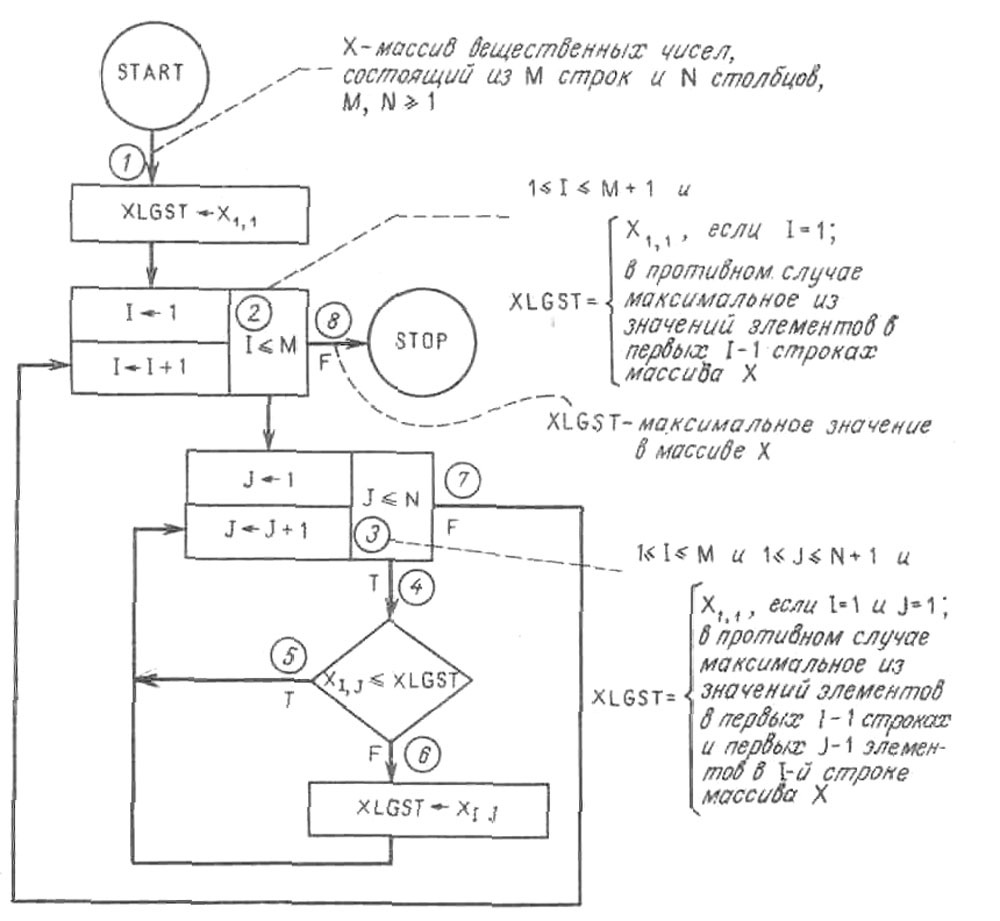
Рис. 7.

2. Путь из точки 2 в точку 3. Предположим, что мы находимся в точке 2 и справедливо связанное с нею утверждение. Перейдем из точки 2 в точку 3. Требуется показать, что при попадании в точку 3 будет справедливо утверждение, связанное с этой точкой. Если мы дошли до точки 3 (из точки 2), то имеем J = 1, а значение XLGST осталось неизменным. Так как N³1, 1 £ J=1 £ N+1, а значение I после точки 2 не изменялось, то 1 £ I £ M + 1. Однако если мы пришли из точки 2 в точку 3, то известно, что проверка 1£M была истинной, и, комбинируя это отношение с 1 £ I £ M + 1, получаем 1 £ I £ M. Если I = 1и J = 1, то из утверждения 2 получим XLGST = X_1,J. В противном случае (т.е. при I¹1) из утверждения 2 получаем, что XLGST равно максимальному из значений элементов в первых I–1 строках массива X или, более точно, максимальному из значений элементов в первых I–1 строках и из значений первые J–1 = 1–1 = 0 элементов в 1-й строке. Таким образом, очевидно, что при переходе из точки 2 в точку 3 утверждение, связанное с точкой 3, оказывается справедливым.

3. Путь из точки 3 через точки 4, 5 к точке 3. Предпо­ложим, что мы находимся в точке 3 и справедливо утверж­дение, связанное с этой точкой. Пройдем через точки 4, 5 к точке 3. Нужно показать, что при возврате в точку 3 соответствующее утверждение останется справедливым. Пусть I и J в исходном положении в точке 3 принимают значения I_N и J_N. Мы имеем 1 £ I_N £ M и 1 £ J_N £ N+1. При возврате в точку 3 через точки 4 и 5 получим I_N+1 = I_N и J_N+1 = J_N + 1. Следовательно, опять имеем 1 £ I_N+1 = I_N £ M. Если мы проходим по этому пути, то проверка J_N £ N была истинной. Из этого, а также из соотношения 1 £ J_N £ N+1 получаем 1 £ J_N £ N. Таким образом, при возврате в точку 3 снова имеем 1< 2 £ J_N+1= J_N + 1£ £ N+1. На всем пути перехода в точку 3 значение XLGST не изменялось, и известно, кроме того, что истинна проверка 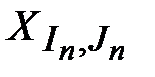£ XLGST. Если учесть истинность утверждения о XLGST до «прохода» по указанному пути, то данное утверждение остается истин­ным и при возврате в точку 3 с I_N+1 = I_N и J_N+1 = J_N + 1. Так как 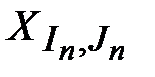£ XLGST, то неизменное значение XLGST снова будет максимальным из значений элементов в первых I_N+1 – 1 = I_N – 1 строках и из значений первых J_N+1 – 1 = (J_N + 1) – 1 = J_N элементов в I_N-й строке массива X.

4. Путь из точки 3 через точки 4, 6 в точку 3. Рассужде­ния для этого пути аналогичны приведенным для предыдуще­го пути, за исключением того, что при возврате в точку 3 XLGST будет иметь значения 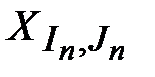. Кроме того, так как выбран этот путь, проверка 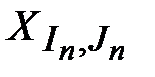£ XLGST была ложной и, следовательно, XLGST < 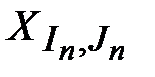. Таким образом, 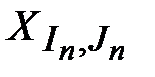больше максимального из значений элементов первых I_N – 1 строк и J_N – 1 элементов в I_N-й строке. Отсюда следует, что при возврате в точку 3 значение XLGST остается максимальным из значений элементов первых I_N+1 –1=I_N –1 строк и первых J_N+1 – 1 = (J_N + 1) – 1 = J_N элементов в I_N-й строке массива X.

5. Путь из точки 3 через точку 7 в точку 2. Предполо­жим, что мы находимся в точке 3 и справедливо соответ­ствующее утверждение. Перейдем из точки 3 через точку 7 в точку 2. Нужно показать, что при возврате в точку 2 будет справедливо связанное с нею утверждение. Из точки 3 в точ­ку 7 мы попадем только тогда, когда ложна проверка J £ N. Но из утверждения, относящегося к точке 3, известно, что 1 £ J £ N+1. Отсюда можно заключить, что J = N+1. Пусть I в точке 3 принимает значение I_N. Утверждение в точке 3 гласит: 1 £ I_N £ M и XLGST равно максимальному из зна­чений элементов в первых I_N – 1 строках и первых J – 1 = (N + 1) – 1 = N элементов в I_N-й строке массива X. Но так как в массиве X существует только N столбцов, то XLGST равно максимальному из значений элементов в I_N строках массива X. Значение XLGST между точками 3 и 2 не изменялось, а значение I изменилось и стало равным I + 1. Так как в точке 3 было справедливо отношение 1£ I_N £ M, то это означает, что 1 < 2 £ I_N+1 = I_N + 1 £ M + 1 справедливо в точке 2. Следовательно, при достижении точки 2 будет справедливо утверждение: XLGST равно максимальному из значений элементов в первых I – 1 = (I_N + 1) – 1 = I_N строках массива X.

6. Путь от точки 2 в точку 8. Предположим, что мы находимся в точке 2, справедливо соответствующее утверж­дение и мы переходим в точку 8. Необходимо показать, что при достижении точки 8 будет справедливо связанное с нею утверждение. Из точки 2 мы перейдем в точку 8, если была ложной проверка 1 £ M. Однако в точке 2 было справедливо неравенство 1£ I £ M+ 1; следовательно, можно заключить, что I= M+1. Значение XLGST при переходе из 2 в 8 не изменялось, и, таким образом, из утверждения, относящегося к точке 2, можно заключить, что при попадании в точку 8 XLGST равно максимальному из значений эле­ментов в первых I – 1 =
= (M + 1) – 1 = M строках массива X. Но массив X содержит только M строк; следовательно, XLGST равно максимальному из значений элементов X.

Таким образом, мы доказали частичную правильность нашей программы. Нам еще осталось удостовериться, что программа закончится. Отметим, что единственными местами в программе, где изменяются I и J, являются «изолирован­ные» части двух итерационных блоков, управляющие увели­чением параметра цикла. Так как значение J увеличивается на 1, а значение N при выполнении внутреннего цикла не изменяется (путь через точки 3, 4, 5, 3 или через точки 3, 4, 6, 3), то значение J должно в конце концов превы­сить значение N. Таким образом, попадая в точку 3, мы когда-нибудь (после конечного числа выполнений внутрен­него цикла) должны попасть в точку 7, а затем в точку 2. При каждом попадании в точку 2 мы затем попадем либо в точку 8 и процесс закончится, либо в точку 3. Если мы попали в точку 3, мы только что видели, как в конце концов дойдем до точки 7 и вернемся в точку 2. При этом зна­чение I будет увеличиваться на 1, а значение M останется неизменным. Следовательно, после конечного числа шагов значение I станет больше значения M. В этот момент мы перейдем из точки 2 в точку 8, и программа закончится. Таким образом, мы доказали конечность нашей программы. Если это доказательство объединить с предыдущим дока­зательством частичной правильности, то отсюда следует полная правильность программы.