Метод индуктивных утверждений

Все блок-схемы, о которых шла речь выше, содержали один-единственный цикл. Основным приемом при доказательстве правильности этих блок-схем было доказательство того, что при попадании во входную точку цикла всегда будет справедливо некоторое утверждение (инвариант цикла). Чтобы доказать это, мы показывали, во-первых, что это утверждение справедливо при первом попадании на вход цикла, и, во-вторых, если мы попали в эту точку и утвержде­ние справедливо, то после выполнения цикла и возврата во входную точку утверждение будет оставаться справедливым. Если структура блок-схемы становится более сложной, например, за счет нескольких вложенных циклов или если существует несколько возможных путей между ключевыми точками, то рассмотренный выше метод уже трудно использовать для доказательства того, что при каждом входе в цикл справедливо соответствующее утверждение.

Предположим, например, что мы имеем дело с блок-схемой общего вида, приведенной на рис. 6.

Наш стандартный прием для доказательства справедливости любого из двух утверждений о циклах в данном случае может оказаться не всегда пригодным. Доказать, что утверждение 1 справедливо при первом попадании в точку 1 вероятно, довольно просто. Однако может оказаться сложным доказательство того, что если мы находимся в точке 1 и справедливо утверждение 1, то при проходе по циклу и возврате в точку 1 утверждение 1 останется справедливым. Трудность заключается в том, что это не просто проход по элементарному циклу и возврат в точку 1. Перед возвратом в точку 1 несколько раз будет выполняться внутренний цикл. Следо­вательно, первым, вероятно, нужно доказать утверждение 2, а затем уже использовать его для доказательства того, что при возврате в точку 1 утверждение 1 останется справедливым. Пытаясь, однако, доказать справедливость утверждения 2 при каждом попадании в точку 2, мы сталкиваемся с аналогичными трудностями. Фактически нужно показать, что при любом попадании в точку 2 из точки 1 (не только в первый момент) будет справедливо утверждение 2. Но для этого скорее всего надо будет знать, что утверждение 1 справедливо, а этого-то мы еще и не доказали.

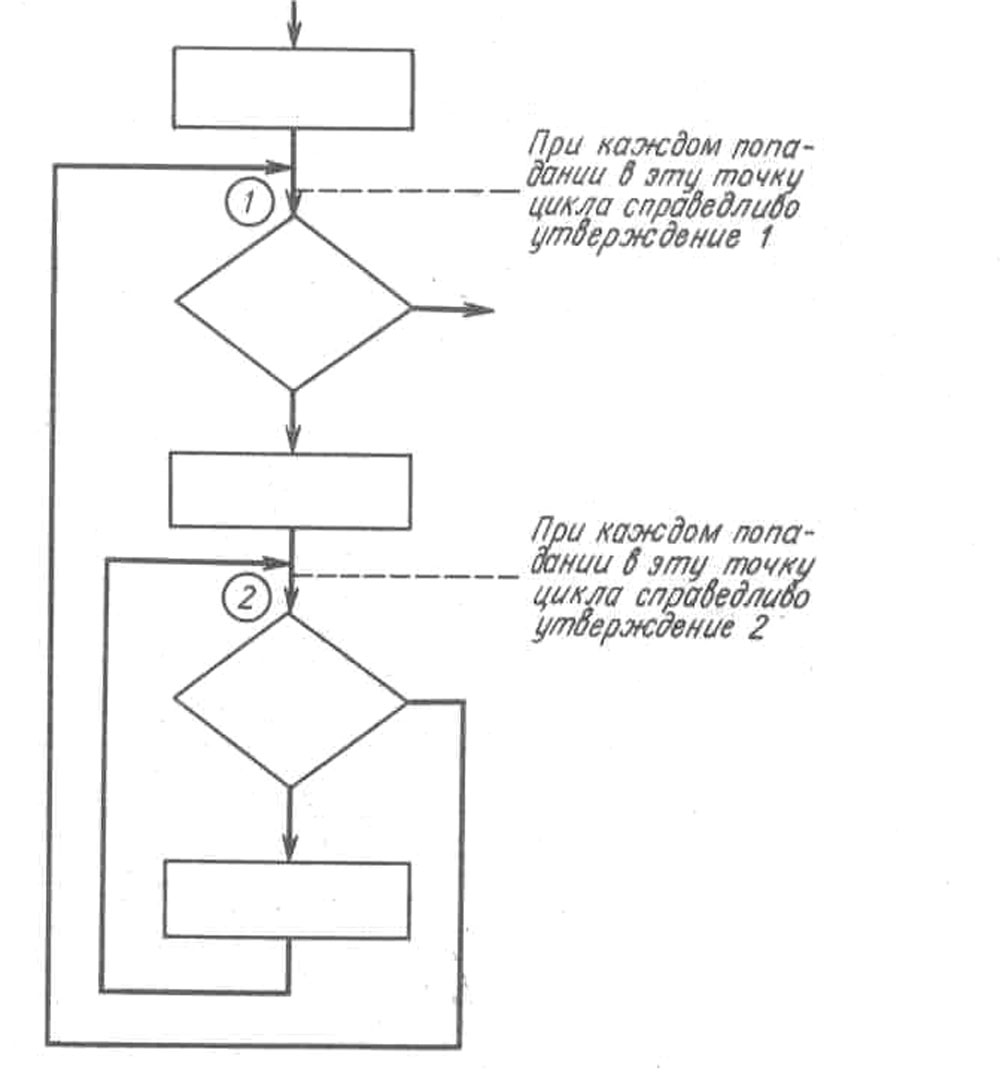
Рис. 6

Для того чтобы устранить эту и аналогичные трудности, нужно обобщить метод доказательства, рассмотренный выше. Обобщенный метод мы назовем методом индуктивных утверждений. Прием, которым мы пользовались выше, есть просто некоторое упрощение этого общего метода, приспособленное для программ, содержащих лишь один-единствен­ный цикл. При доказательстве правильности программ методом индуктивных утверждений доказательство конечности программы (в смысле конечности времени выполнения программы, а не ее размера) проводится отдельно от доказательства справедливости некоторых ключевых утверждений при достижении соответствующих точек программы. Для уточнения использованных понятий дадим два определения.

Определение 1. Пусть А – некоторое утверждение, описывающее предполагаемые свойства данных в программе (блок-схеме), а С – утверждение, описывающее то, что мы по предположению должны получить в результате процесса выполнения программы (т. е. утверждение о правильности). Будем говорить, что программа частично правильна (по отношению к А и С), если при каждом выполнении ее с данными, удовлетворяющими предположению А, будет справедливо утверждение С при условии, что программа закончится. Другими словами, если выполнять программу с данными, удовлетворяющими А, то либо она не заканчивает­ся, либо заканчивается и удовлетворяется утверждение С.

Таким образом, программа может быть частично правильна, даже если она не заканчивается при некоторых (или всех) входных данных, удовлетворяющих А. Необходимо только, чтобы, если уж программа заканчивается, было справедливо утверждение С с данными, удовлетворяющими А.

Определение 2. Будем называть программу (блок-схему) полностью правильной (по отношению к А и С), если она частично правильна (по отношению к А и С) и заканчивается при всех данных, удовлетворяющих А.