Основные принципы доказательства правильности для блок-схем

Если мы хотим доказать, что некоторая программа правильна или верна, то прежде всего должны уметь описать то, что по предположению делает эта программа. Назовем такое описание высказыванием о правильности или просто утверждением. В этом случае доказательство правильности состоит из доказательства того, что программа, будучи запущенной, в конце концов окончится (выполнится оператор STOP), и после окончания программы будет справедливо утверждение о правильности. Часто требуется, чтобы программа работала правильно только при определенных значениях входных данных. В этом случае доказательство правильности состоит из доказательства того, что если программа выполняется при соответствующих входных данных, то она когда-либо закончится, и после этого будет справедливо утверждение о правильности.

Алгоритм доказательства правильности блок-схемы включает следующие шаги:

1. Расставить на блок-схеме контрольные точки.

2. Сформулировать и расставить к соответствующим точкам четыре индуктивных утверждения (утверждение о входных данных, инвариант цикла, утверждение о конечности цикла и утверждение о правильности), причем инвариант цикла выводится с помощью трассировочной таблицы.

3. Доказать инвариант цикла с помощью простой индукции.

4. Неформально доказать утверждение о конечности.

5. Доказать что из инварианта цикла и утверждения о конечности следует утверждение о правильности.

Проиллюстрируем эти идеи на примере доказательства правильности для блок-схемы очень простой программы.

Пример 2.1. Докажем, что приведенная на рис.2 блок-схема правильна, т. е. если ее начать выполнять с M и N, имеющими некоторые целые значения, причем M³0, то выполнение в конечном итоге закончится с J = M • N.

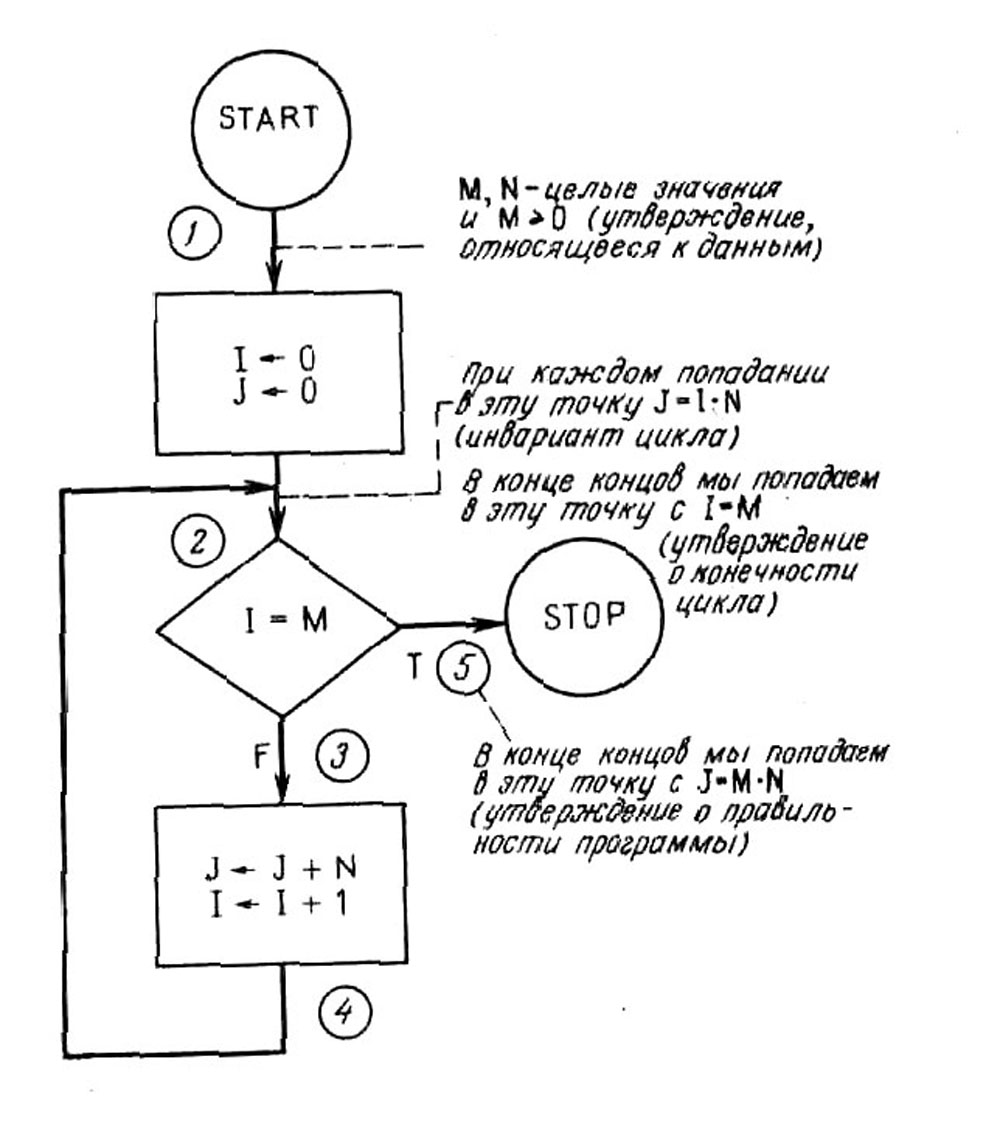
Рис. 2.

Вначале докажем, что при попадании в точку 2 J=I•N.

1. При первом попадании в точку 2 при переходе из точки 1 имеем I=0 и J=0. Таким образом, утверждение J = I•N = 0•N = 0 справедливо.

2. Предположим, что мы попали в точку 2 и утверждение J = I • N справедливо. Пусть I и J в этой точке принимают значения I_N и J_N, т.е. J_N = I_N• N. Предположим теперь, что мы прошли по циклу (от точки 2 через точки 3, 4 вновь в точку 2). При возвращении в точку 2 I и J принимают новые значения I_N₊₁ и J _N₊₁, которые можно представить следующим образом:

I_N₊₁ = I_N + 1,

J_N+1 = I_N• N+ N = (I_N + 1) • N = I_N₊₁• N. (Так как J_N = I_N• N)

Следовательно, при очередном попадании в точку 2 высказывание J=I• N вновь справедливо, что и требовалось доказать, т. е. при любом попадании в точку 2 справедливо высказывание J = I • N.

Теперь докажем, что в конце концов попадем в точку 2 со значением I=M. При первом попадании в точку 2 имеем I=0. При последующих попаданиях, если таковые есть, I каждый раз увеличивается на 1. Так как значение M нигде в программе не изменяется и мы предположили, что M³0, то очевидно, что в какой-то момент I станет равным M.

Если мы попадем в точку 2 при I = M, то будет верно и J = I • N = M • N. Отношение I = M в этот момент истинно, и мы попадаем по стрелке с пометкой Т (TRUE – истина) в точку 5 с J = M • N. На этом доказательство правильности программы заканчивается..

Пример 2.2. Докажем правильность программы вычисления целого частного IQ и остатка IR от деления J1 на J2, где J1 и J2 – любые два целых числа, удовлетворяющие условиям 0 £ J1 и 1 £ J2. Операция деления в программе для вычисления IQ и IR не используется. Один из способов указать, что делает программа, – сказать, что она вычисляет два целых числа IQ и IR, таких, что J1 /J2 = IQ + IR/J2 и 0 £ IR < J2. Это можно записать так: J1 = IQ • J2 + IR и 0£IR<J2. Как и выше, свяжем непосредственно с блок-схемой программы (рис. 3) допущения о входных данных и те утверждения, правильность которых требуется доказать.

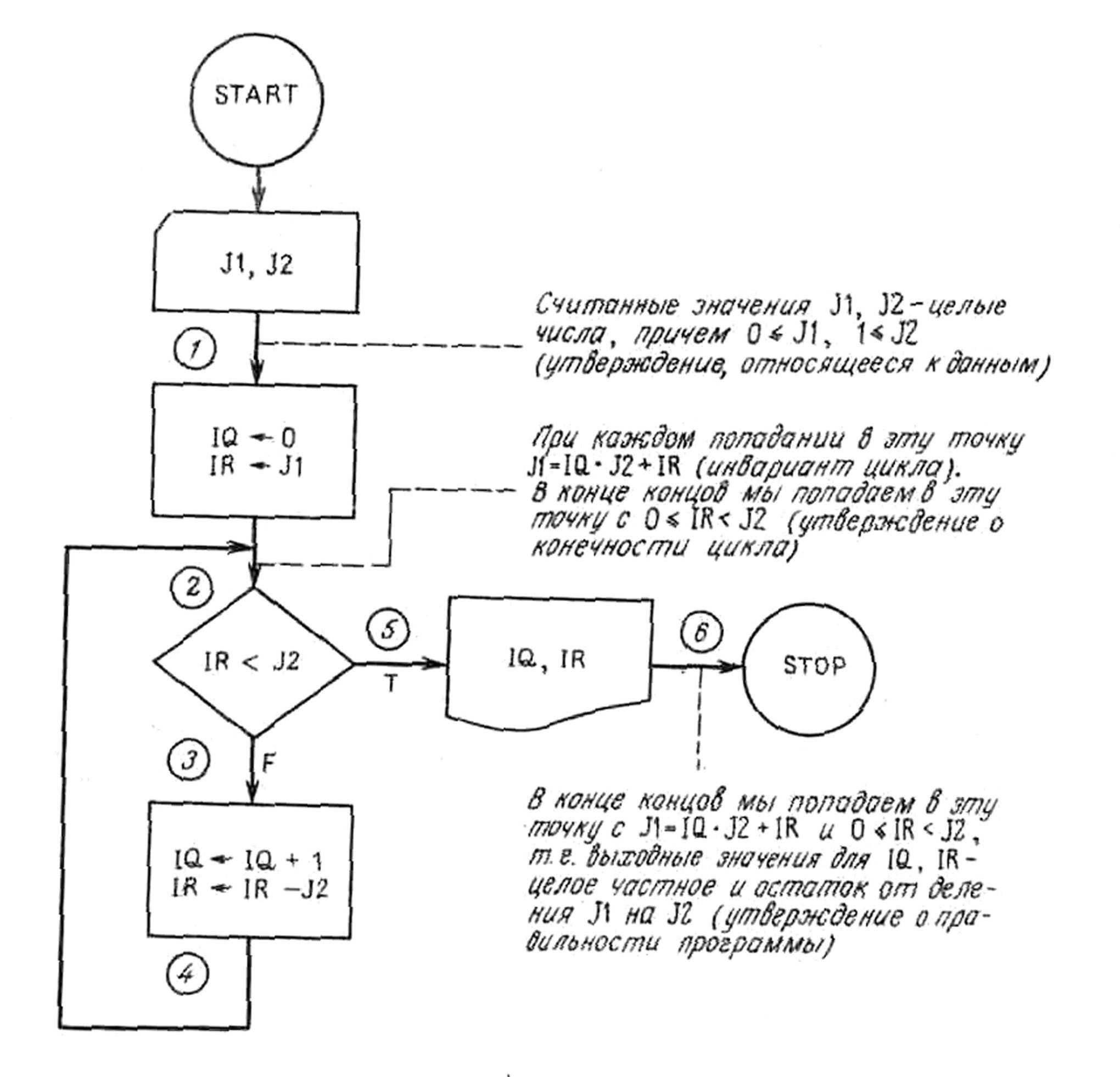рис. 3.

Отметим, что допущения о считываемых значениях для J1 и J2 мы поставили непосредственно после ввода. Это указывает на то, что правильность работы программы будет доказываться только для данных, удовлетворяющих этому допущению. Утверждение о правильности блок-схемы связано с ее последней точкой. Кроме того, с начальной точкой цикла связываются два основных факта, которые требуется доказать. Теперь проследим за работой программы с символическими данными для J1 и J2 и выясним, как ведут себя инварианты цикла (основные утверждения о цикле):

Число проходов Значение IQ Значение IR

через точку 2

1 0 J1

2 1 J1 – J2

3 2 J1 – 2 • J2

4 3 J1 – 3 • J2

… … …

. . Пока IR < J2

Отметим, что при каждом попадании в точку 2

IR = J1 – IQ • J2, или J1 = IQ • J2 + IR.

Это утверждение идентично утверждению о правильности, за исключением того, что последнее еще включает условие 0 £ IR < J2. Таким образом, остается лишь показать, что цикл когда-нибудь закончится и при этом будет выполняться условие 0 £ IR < J2. Легко установить, что высказывания, связанные с точкой 2, утверждают именно эти факты о цикле.

Для доказательства правильности программы сначала покажем, что, как только мы попадем в точку 2, J1 = IQ • J2 + JR.

1. При первом проходе через точку 2, двигаясь от точки START к точке 2, имеем IQ = 0 и IR = J1, т. е. утверждение J1 = IQ • J2 + IR = 0 • J2 + J1 = J1 справедливо.

2. Предположим, что выполнение программы дошло до точки 2 и справедливо утверждение J1 = IQ • J2 + IR. Пусть IQ и IR в этот момент принимают значения IQ_N и IR_N. Наше справедливое по предположению утверждение записывается так: J1 = IQ_N • J2 + IR_N (гипотеза индукции). Пройдем один раз по циклу (от точки 2 через точки 3, 4 опять в точку 2). При возвращении в точку 2 новые значения IQ и IR будут такими: IQ_N₊₁ = IQ_N + L и IR_N₊₁ = IR_N – J2. Таким образом,

IQ_N₊₁ • J2 + IR_N₊₁ = (IQ_N + 1) • J2 + (IR_N – J2) =

IQ_N •J2 + J2 + IR_N – J2 = IQ_N •J2 + IR_N = J1,

(По гипотезе индукции)

Что и требовалось доказать, т. е. при попадании в точку 2 справедливо высказывание J1 =IQ • J2 + IR.

Докажем, что в конце концов мы попадем в точку 2 при условии 0 £ IR < J2. Для этого покажем вначале, что при всяком проходе через точку 2 имеем 0 £ IR.

1. При первом проходе через точку 2 имеем IR=J1 и по предположению 0£J1. (Отметим, что это единственное место в доказательстве, где используется данное предположение. Таким образом, если бы мы не потребовали IR³0, то блок-схема должна была бы работать правильно даже для отрицательных значений J1.)

2. Предположим, что мы попали в точку 2 и 0 £ IR. Пусть в этот момент IR принимает значение IR_N. Если мы через цикл вернемся вновь в точку 2, то IR примет новое значение IR_N₊₁ =IR_N – J2. Но через цикл мы пройдем только в случае отрицательного ответа на проверку IR_N < J2, т. е. если истинно отношение J2 £ IR_N. Но если J2 £ IR_N, то 0 £ IR_N – J2 = IR_N₊₁ истинно. Таким образом, мы доказали, что 0 £ IR при каждом попадании в точку 2.

Докажем затем, что в конечном итоге мы попадем в точку 2 при справедливом условии IR < J2 (т. е. в этом случае мы будем иметь 0 £ IR < J2). Отметим, что при каждом проходе через цикл значение IR уменьшается на значение J2. Так как значение J2 в программе нигде не изменяется и так как 1 £ J2, то, очевидно, при каждом повторении процесса IR уменьшается по крайней мере на 1. Следовательно, в конце концов значение IR должно стать меньше J2 (с помощью метода индукции это можно доказать более строго).

Таким образом, в какой-то момент мы попадем в точку 2 со справедливыми условиями 0 £ IR < J2 и J1 =IQ • J2 + IR. В этот момент условие IR<J2, естественно, истинно, и из точки 2 мы идем в точку 5, а затем в точку 6. Так как на пути из точки 2 в точку 6 ни одна переменная не изменяется, то очевидно, что в момент прихода в точку 6 утверждение о правильности будет справедливо. Следовательно, мы доказали, что при выполнении программы с целыми J1 и J2, удовлетворяющими условиям 0 £ J1 и 1 £ J2, программа в какой-то момент закончится, и будут справедливы отношения J1 = IQ • J2 + IR и 0£IR<J2, т, е. IQ и IR будут целыми частным и остатком от деления J1 на J2.

Пример 2.3. Мы хотим доказать, что приведенная на рис. 4 блок-схема обеспечивает правильное вычисление суммы 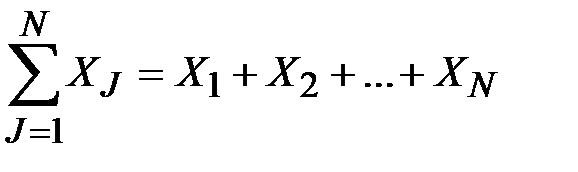. Покажем, что при каждом попадании в точку 2 выполняются соотношения 1 £ I £ N+1 и .

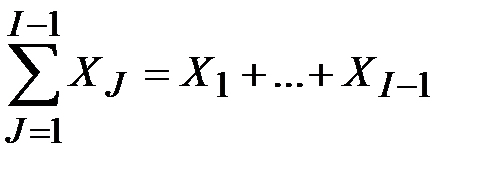1. При первом попадании в точку 2 имеем I = 1 и SUM =0; следовательно, утверждения, что 1 £ I < N + 1 и SUM = 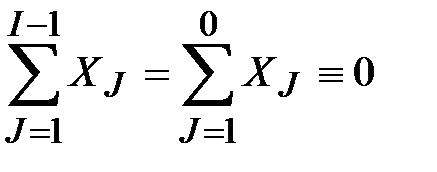, справедливы.

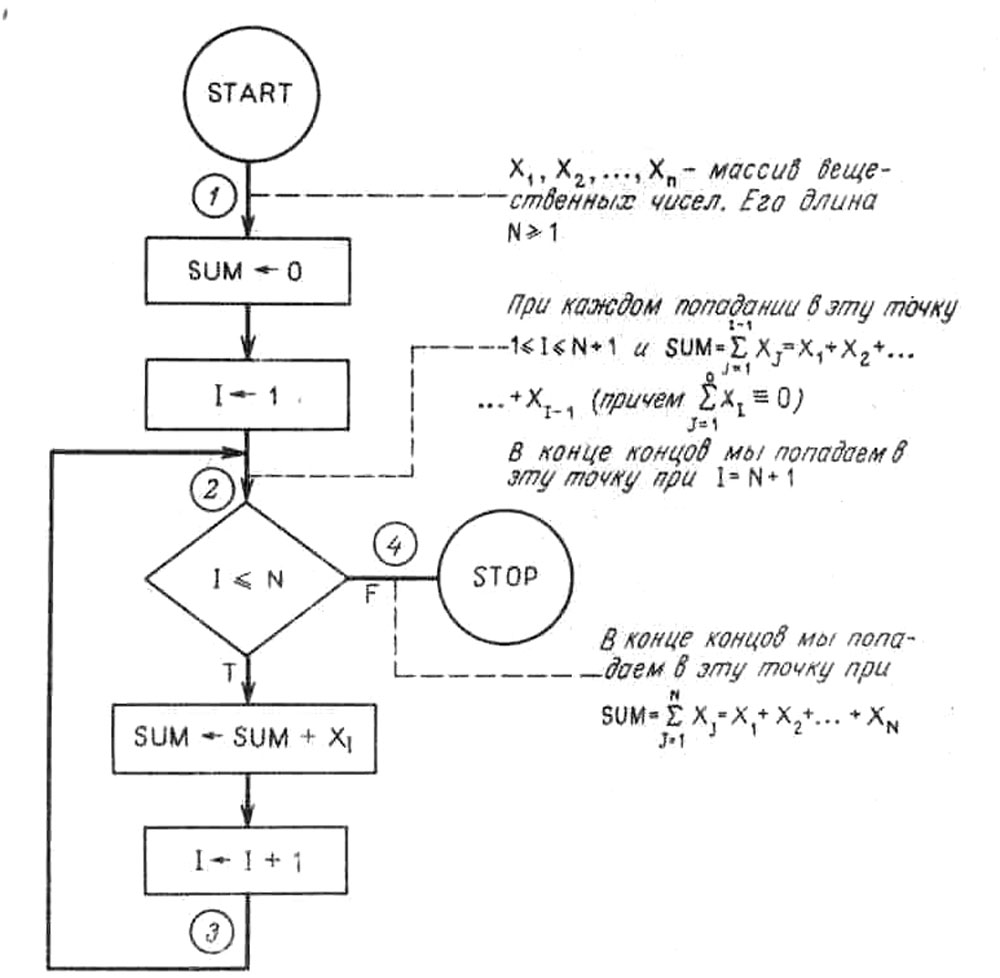
Рис. 4

2. Предположим, что мы находимся в точке 2 и 1 £ I £ N + 1 и SUM= 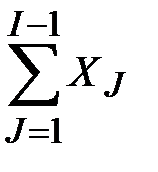справедливы. Пусть I и SUM в этой точке принимают значения I_N и SUM_N, т.е.
1 £ I_N £ N + 1 и = 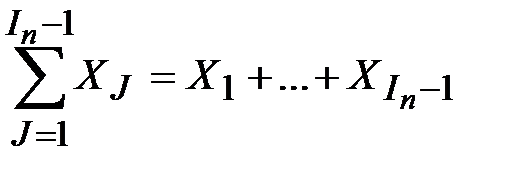. Если мы пройдем по циклу и вернемся в точку 2, то получим I_N₊₁ =I_N+ 1 и SUM_N₊₁= SUM_N + +

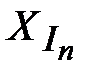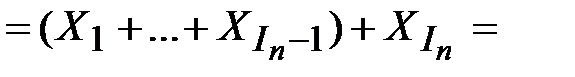
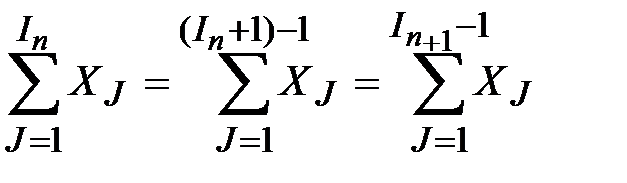
Кроме того, если цикл повторялся, то проверка I_N £ N давала положительный ответ, а так как истинно и утверждение 1£ I_N £ N+1, то, следовательно, 1£ I_N £N. Но в этом случае при возврате в точку 2 имеем
1 < 2 £ I_N + 1 = I_N₊₁£ N+ 1. Таким образом, справедливость утверждений
1 £ I £ N + 1 и SUM= 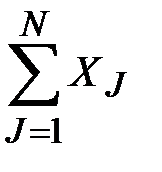при прохождении точки 2 доказана.

Легко видеть, что если 1 £ N, то переменная I, увеличиваясь с 1 каждый раз на 1, в конце концов станет равной N+ 1. В этот момент проверка даст отрицательный ответ и мы попадем в точку 4, где имеем SUM= 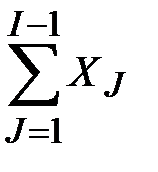и I=N+1, или, что тоже самое, SUM = 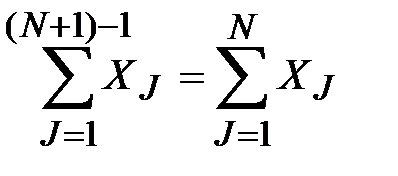. Таким образом, мы доказали, что работа программы (достигнув точки 4) прекратится и SUM = .

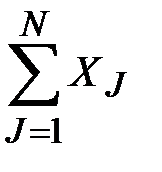Пример 2.4. Мы хотим доказать, что приведенная на рис. 5 блок-схема вычисляет и печатает среднее значение и максимальное из всех чисел во входном файле. Сначала докажем, что справедливо утверждение, связанное с точкой 2.

1. Если программа выполняется с входным файлом, содержащим одно и более вещественных чисел, то можно выполнять первый блок (так как входной файл не пуст), и при первом попадании в точку 2 значение N равно 1, а значение XLGST и SUM – первые числа в исходном входном файле. Таким образом, при первом достижении точки 2 утверждения о N, XLGST и SUM справедливы.

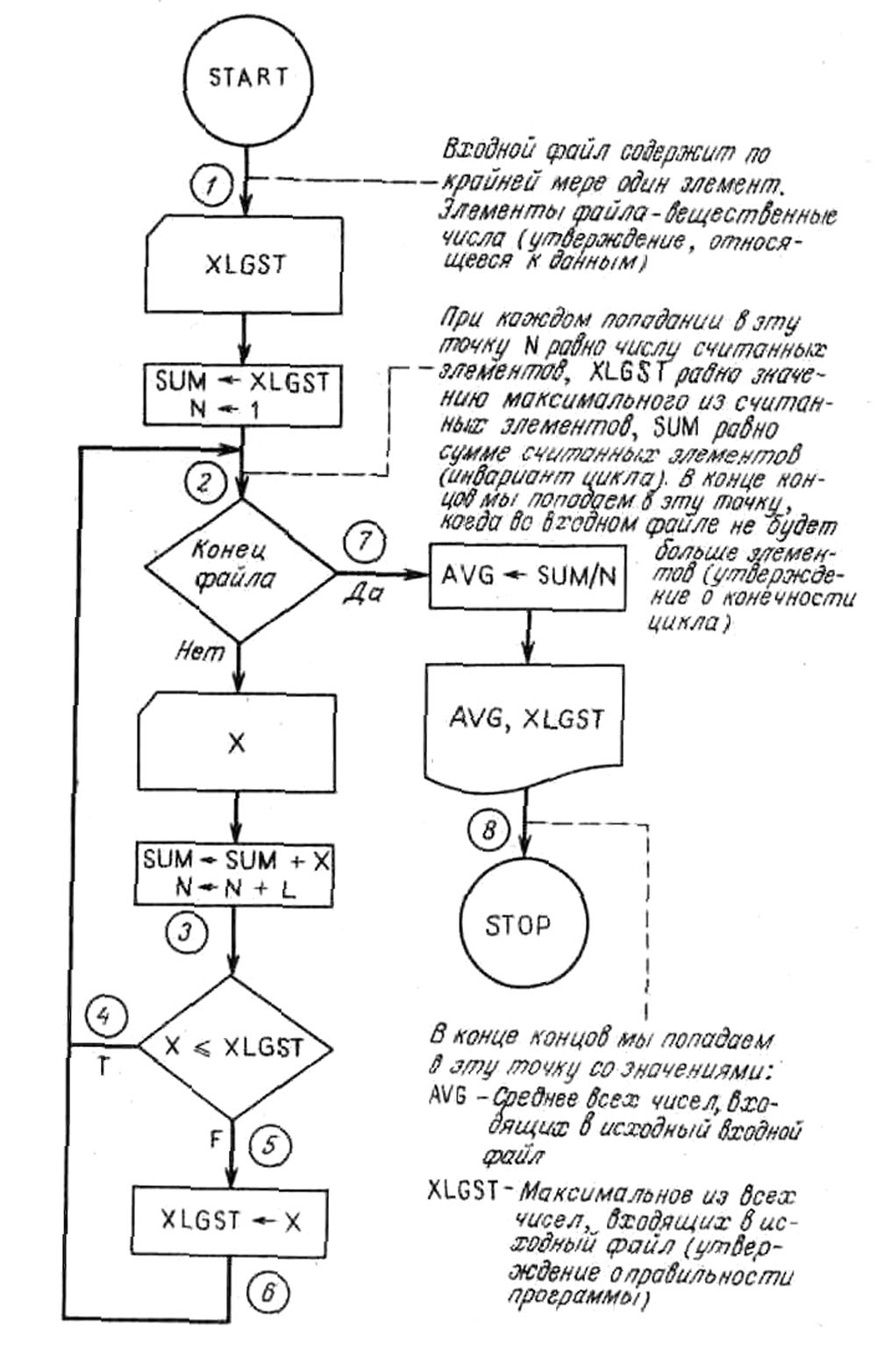
Рис. 5

2. Предположим, что мы находимся в точке 2 и утверждения о N, XLGST и SUM справедливы. Нужно показать, что, если мы пройдем по циклу и вернемся в точку 2, эти утверждения будут оставаться верными. Отметим, что при прохождении цикла в X считывается очередное значение из входного файла (файл по определению не пуст, иначе цикл не выполнялся бы), значение N увеличивается на 1, а значение SUM становится SUM + Х. Поэтому при возврате в точку 2 значение N вновь указывает число считанных из входного файла данных (больше предыдущего на 1), а значение SUM вновь будет суммой всех считанных из файла чисел (сумма всех предварительно считанных чисел плюс последнее прочитанное число). Затем при каждом выполнении цикла переменная XLGST (мы предполагаем, что это наибольший из всех считанных элементов) сравнивается с новым элементом, считанным последним в X из файла. Если отношение Х £ XLGST истинно, то по блок-схеме XLGST не изменяется, и это верно, так как ее новое значение представляет собой самое большое число из всех считанных из файла. Если же отношение Х £ XLGST ложно, то последний считанный элемент – самый большой из всех считанных, и поэтому в блок-схеме предусмотрена запись значения X в XLGST. Таким образом, при возврате в точку 2 (пройдем ли мы в нее через точки 2, 3, 4 или через точки 2, 3, 5, 6) XLGST всегда будет наибольшим из всех считанных до этого значений, что и требовалось доказать, т. е. при каждом проходе через точку 2 утверждения, касающиеся N, XLGST и SUM, справедливы.

Ясно, что в конце концов мы попадаем в точку 2, когда во входном файле не останется больше элементов, которые можно было бы прочитать. Это произойдет потому, что при каждом прохождении цикла считывается один очередной элемент файла, а мы (неявно) предполагали, что входной файл содержит конечное число элементов. Следовательно, после конечного числа прохождений через цикл все элементы входного файла будут прочитаны. После этого проверка на конец файла даст ответ ДА, и мы выйдем из цикла, имея следующие значения: N – число элементов чисел, считанных на данный момент; XLGST – наибольший из всех элементов в исходном входном файле; SUM – сумма всех элементов в исходном входном файле.

При попадании в точку 8 переменная AVG будет иметь значение
AVG =SUM/N, a XLGST – то же значение, которое указано выше. Таким образом, работа программы в конце концов закончится, и, когда это произойдет, AVG и XLGST будут иметь требуемые значения.

<456 7 8 9 10 >

Дата добавления: 2016-04-11; просмотров: 1582;