Затухающие колебания
Свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются (энергия переходит в теплоту вследствие трения в механических колебательных системах).
Для пружинного маятника сила трения пропорциональна скорости
Fmp = -rυ = - r 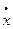 , где r – коэффициент сопротивления
, где r – коэффициент сопротивления
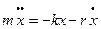
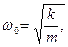 где
где 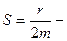 коэффициент затухания.
коэффициент затухания.
Дифференциальное уравнение затухающих колебаний маятника
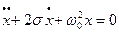
Закон затухания математического маятника
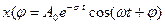 , где
, где 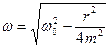 .
.
Величины характеризующие затухающие колебания.
A(t) = A0 e-σt – уравнение затухания амплитуды
S – коэффициент затухания
τ = 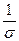 - промежуток времени в течение, которого амплитуда уменьшается в е раз, называется временем релаксации.
- промежуток времени в течение, которого амплитуда уменьшается в е раз, называется временем релаксации.
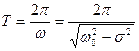
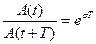 - декремент затухания
- декремент затухания
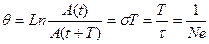 - логарифмический декремент затухания.
- логарифмический декремент затухания.
Ne – число колебаний, совершаемых за время уменьшения амплитуды в е раз.
Q – добротность
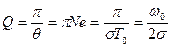
Выводы
1. Гармонические колебания – колебания, которые совершаются по закону синуса (косинуса)
x (t) = A cos (ω0 t + φ)
2. Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением
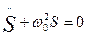
3. Полная энергия 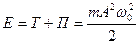
4. Дифференциальное уравнение затухающих колебаний маятника
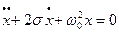 .
.
Дата добавления: 2016-04-11; просмотров: 559;
