Частые случаи колебаний маятника
Гармонические колебания
 |
Колебаниями называются движения или процессы, которые характеризуются повторяемостью во времени.
 |
Колебания (разной физической природы)
Свободные (совершаются за счет Вынужденные
первоначально сообщенной энергии)
Гармонические колебания – колебания, которые совершаются по закону синуса (косинуса)
x (t) = A cos (ω0 t + φ)
А – максимальное значение колеблющейся величины;
ω0 – круговая частота;
φ – начальная фаза колебания;
(ω0 t + φ) – фаза колебания в момент времени t.
Т – период колебания.
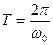
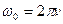 .
.
Частые случаи колебаний маятника
Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением
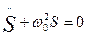
Колебания гармонического осциллятора являются важным примером периодического движения и служит моделью в классической и квантовой физике.
1) Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы.
F = - kx, где k – жесткость пружины 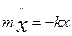 .
.
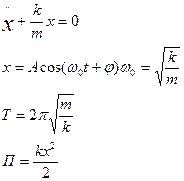
2) Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку о, не совпадающую с центром масс i тела.
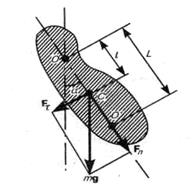
| Уравнение движения физического маятника 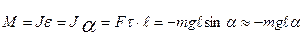 ,
где J - момент инерции маятника относительно оси, проходящей через точку подвеса ,
где J - момент инерции маятника относительно оси, проходящей через точку подвеса
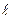 - расстояние между ней и центром масс маятника. - расстояние между ней и центром масс маятника.
|
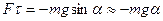 - возвращающая сила
- возвращающая сила
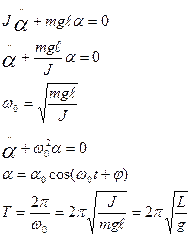
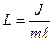 - приведенная длина физического маятника
- приведенная длина физического маятника
Точка 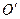 на продолжении прямой ОС, отстоящий от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качания физического маятника.
на продолжении прямой ОС, отстоящий от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качания физического маятника.
3) Математический маятник – это идеализированная система, состоящая из материальной точки m, подвешенной на нерастяжимой невесомой нити, колеблющая под действием силы тяжести.
Момент инерции математического маятника J = m 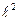 ,
, 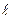 - длина маятника
- длина маятника
T = 2π 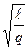 - период математического маятника.
- период математического маятника.
Приведенная длина физического маятника – это длина такого маятника, период колебаний которого совпадает с периодом колебаний физического маятника.
Энергия колебаний
Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии.
Уравнение движения гармонических колебаний
x=A cos (ω0 t + φ)
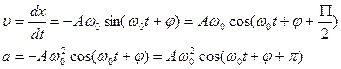
Сила F = ma, действующая на колеблющуюся материальную точку массой m равна F = - m 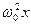 .
.
Сила, действующая на материальную точку, направлена в противоположную сторону.
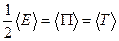
Кинетическая энергия материальной точки, совершающий прямолинейные гармонические колебания
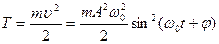
Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна
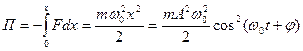
Полная энергия 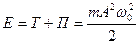
Дата добавления: 2016-04-11; просмотров: 919;
