Расчет червячных передач на контактную прочность

Червяки изготавливают из сталей типа 20Х, 18ХГТ с твердостью после цементации 57 ÷ 64 HRC, а также сталей типа 45, 40Х, 40ХН с поверхностной закалкой до твердости 45 ÷ 55 HRC. Во всех случаях необходима шлифовка и полировка витков червяка.

Червяк проверяют на жесткость, рассматривая его как балку на двух опорах. При помощи эпюр изгибающих и крутящих моментов определяют наиболее опасное сечение и определяют стрелу прогиба, которая не должна превышать допустимое значение: μ ≤ [ μ], где [ μ] = (0,005 ÷ 0,007)m_.

В процессе эксплуатации в червячных передачах чаще наблюдается износ и заедание, а не усталостное выкрашивание, как у зубчатых передач. Повышенный износ связан с большими скоростями скольжения. Поэтому для предупреждения износа и заедания ограничивают значение контактных напряжений и применяют специальные антифрикционные материалы. При скоростях скольжения 5 ÷ 25 м/с используют оловянистые бронзы (типа БрО10Ф1 и др.); при скоростях 2 ÷ 5 м/с – безоловянистые бронзы (типа БрА9Ж3Л и др.); при скоростях до 2 м/с – чугуны типа СЧ15, СЧ18.

Так как износ и заедание зависит от величины контактных напряжений, то основным критерием работоспособности червячных передач является контактную прочность зубьев червячного колеса.

По аналогии с расчетом зубчатых передачами наибольшие контактные напряжения определяют по формуле Герца

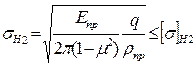
(4.90)

где Е_пр – приведенный модуль упругости; μ – коэффициент Пуассона; q – нормальная нагрузка; ρ_пр – приведенный радиус кривизны боковой поверхности зуба колеса.

Приведенный модуль упругости

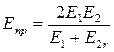
(4.91)

где E₁ = 2,1·10⁵ МПа – модуль упругости стального червяка; E₂ = 0,9·10⁵ МПа – модуль упругости бронзы.

Коэффициент Пуассона μ = 0,3.

Нормальная нагрузка на единицу длины контактных линий

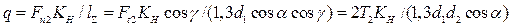
(4.92)

где F_n2 – нормальная нагрузка по формуле (4.89); l_Σ ≈ 1,3d₁/cosγ – суммарная длина контактных линий витков червяка и зубьев колеса; К_Н – коэффициент нагрузки.

Радиус кривизны профиля витка червяка ρ₁ = ∞, поэтому приведенный радиус кривизны червячной пары, соответствует радиусу кривизны боковой поверхности зуба колеса

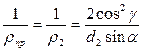
(4.93)

Подставляя эти значения в формулу Герца, после преобразований получим формулу проверочного расчета

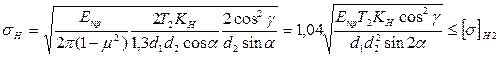
(4.94)

С учетом равенства (4.73), (4.77) и (4.82) можно получить следующее уравнение проверочного расчета

,

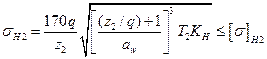(4.95)

где q – коэффициент диаметра червяка; z₂ – число зубьев колеса.

Решив это уравнение относительно межосевого расстояния, получим приближенное уравнение проектировочного расчета

.

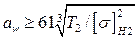(4.96)

Значение а_w согласуем со стандартным рядом.