КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ

План лекции

1. Общие сведения.
2. Расчет на контактную прочность.
3. Расчет на изгибную выносливость.

1. Общие сведения

Применяются в передачах, оси валов которых пересекаются под межосевым углом Σ = 90⁰.

Конические колеса бывают с прямыми и круговыми зубьями.

Основное преимущество этих передач – возможность передавать нагрузку при перпендикулярных осях.

Основные недостатки – более сложная технология изготовления и монтажа. Для нарезания зубьев требуются специальные станки и инструменты. Кроме допусков на размеры необходимо выдерживать допуски на углы делительных конусов δ₁ и δ₂. Также в этих передачах затруднено размещение опор. Поэтому одно из колёс выполняется на консольном валу, что увеличивает нагрузки на валы и опоры.

По опытным данным, нагрузочная способность конической прямозубой передачи составляет ≈ 0,85 цилиндрической. Однако, несмотря на это она имеет широкое применение в машиностроении.

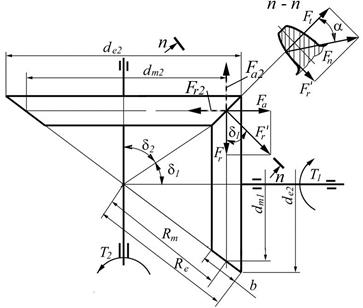
Рисунок 4.13 – Схема конического зацепления

Передаточное число при межосевом угле Σ = 90⁰ определяют по выражениям:

.

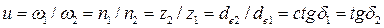(4.52)

Основные геометрические размеры прямозубых конических передач зависят от модуля и числа зубьев. При этом модуль является переменной величиной. В этой связи размеры конических колес определяют по внешнему торцу зуба и его средней части.

В качестве основного принимают внешний окружной модуль m_e и средний модуль m ≈ 0,857m_e. При известном числе зубьев шестерни и колеса определяют:

внешний делительный диаметр

; ;

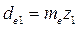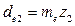(4.53)

внешнее конусное расстояние

;

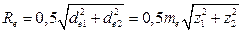(4.54)

среднее конусное расстояние

,

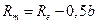(4.55)

где b – ширина зубчатого венца колеса;

,

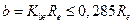(4.56)

где K_be – коэффициент ширины зубчатого венца;

средние делительные диаметры

; .

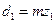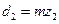(4.57)

Силы в зацеплении определяют по размерам в среднем сечении зуба шестерни (рисунок 4.13). По этой схеме окружные силы

.

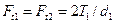(4.58)

Радиальная сила на шестерне и осевая на колесе

;

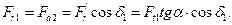(4.59)

Осевая сила на шестерне и радиальная на колесе

.

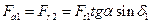(4.60)

Форма зубьев конических колес в нормальном сечении такая же, как у цилиндрических, поэтому прямозубое коническое колесо может быть приведено к эквивалентному цилиндрическому. При этом диаметры эквивалентных колес

; ,

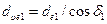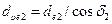(4.61)

а число зубьев

; .

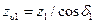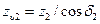(4.62)

1. Расчет на контактную прочность

Расчет зубьев прямозубых конических передач по контактным напряжениям проводим по той же методике, что и цилиндрических зубчатых передач. В основе расчета лежит формула Герца

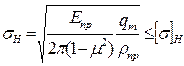
(4.63)

где Е_пр – приведенный модуль упругости материала колес; μ – коэффициент Пуассона; q_m – удельная нагрузка; ρ_пр – приведенный радиус кривизны боковой поверхности зубьев.

Удельная нагрузка распределяется неравномерно по длине зуба конических колес, поэтому за расчетное принимается среднее сечение зуба с нагрузкой q_m:

.

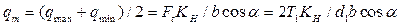(4.64)

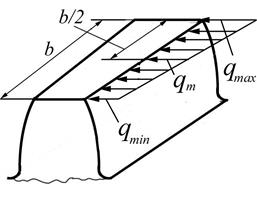
Рисунок 4.14 – Схема нагружения зуба

Приведённый радиус кривизны также определяем для среднего сечения зуба с учетом диаметров эквивалентных колес (4.61):

.

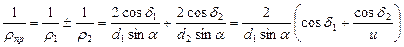(4.65)

Применяя подстановки

; ,

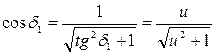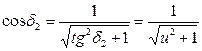(4.66)

получим

.

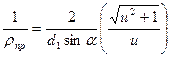(4.67)

Сравнительный анализ полученных зависимостей и аналогичных зависимостей для прямозубых цилиндрических передач показывает, что отличие имеет место только в формуле (4.67) – вместо (u ± 1) используется выражение 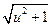. Поэтому формула для проверочного расчета (4.14) будет иметь вид

.

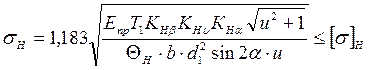(4.68)

где Θ_H = 0,85 – поправочный коэффициент, который указывает на пониженную контактную прочность зубьев конических колёс по сравнению с цилиндрическими.

В качестве проектного параметра удобно использовать внешний делительный диаметр колеса. После преобразований выражения (4.68) можно получить

.

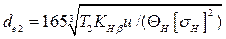(4.69)

Значения d_e2 регламентированы ГОСТ 12289 – 76.

1. Расчет на изгибную выносливость

Расчет на изгибную прочность конических прямозубых колес выполняют по зависимости, аналогичной прямозубой цилиндрической передаче (выражение 4.26):

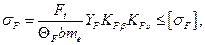
(4.70)

где Θ_F – коэффициент вида конических колес (для прямозубых колес Θ_F = 0,85; для колес с круговыми зубьями Θ_F = 1,0). Остальные параметры имеют то же значения, что и у исходной формулы.

В качестве проектного параметра обычно используют внешний окружной модуль. После преобразований выражения (4.70) можно получить

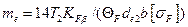
(4.71)

Полученное значение m_e можно не округлять до стандартного значения. При этом в силовых конических передачах рекомендуется принимать m_e ≥ 1,5 мм.