ПРЯМОЗУБЫЕ ЦИЛИНДРИЧЕСКИЕ ПЕРЕДАЧИ

План лекции

1. Расчет на контактную прочность.
2. Расчет на изгибную выносливость.

1. Расчет на контактную прочность

Известно, что поверхностное разрушение зубьев является основной причиной выхода строя, поэтому контактная прочность является основным критерием работоспособности зубчатых передач. В этой связи, зубчатые колёса рассчитывают по контактным напряжениям, а проверку ведут по напряжениям изгиба.

В прямозубых колесах зубья входят в зацепление сразу по всей длине. Это явление сопровождается ударами и шумом, особенно при высоких скоростях.

Расчет на контактную прочность выполняют, полагая, что зацепление пары зубьев происходит в полюсе, т.е. в зоне наибольшего давления.

Контакт в полюсе можно рассматривать как контакт двух цилиндров с радиусом ρ₁ и ρ₂ (рисунок 4.3). В этом случае справедлива формула Герца для контактных напряжений

(4.7)

где Е_пр – приведенный модуль упругости; μ – коэффициент Пуассона; q – удельная нагрузка; ρ_пр – приведенный радиус кривизны боковых поверхностей зубьев.

Для прямозубых передач удельная нагрузка (рисунок 4.4)

,

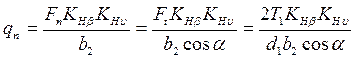(4.8)

где Т₁ – момент крутящий на шестерне; d₁ – делительный диаметр шестерни; b₂ – ширина венца колеса.

Приведённый радиус кривизны боковых поверхностей зубьев

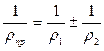
(4.9)

На основании схемы, показанной на рисунке 4.4

,

(4.10)

где u – передаточное число.

Приведённый модуль упругости материала

,

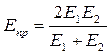(4.11)

где Е₁ и Е₂ – модуль упругости материала шестерни и колеса. Для стальных колес E_{п р} = E.

Подставив эти значения в формулу Герца, получим

,

(4.12)

Произведя сокращения и применяя подстановку cosα ∙ sinα = sin2α/2, получим для нормального зацепления

,

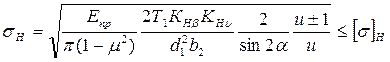(4.13)

Вынося из-под корня постоянные значения и принимая μ = 0,3, получим итоговое уравнение проверочного расчета

.

(4.14)

Из уравнения (4.13) также можно получить стандартное уравнение проверочного расчета (ГОСТ 21354-87). Для этого обозначим сомножители, входящие в подкоренное выражение как:

,

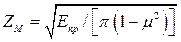(4.15)

- коэффициент, учитывающий механические свойства материала сопряженных колес (для стальных зубчатых колес Z_M = 275);

(4.16)

- коэффициент, учитывающий форму сопряженных поверхностей зубьев (для прямозубых передач Z_H = 1,76);

,

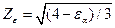(4.17)

- коэффициент, учитывающий суммарную длину контактных линий (для прямозубых колес Z_ε = 0,9).

Обозначим также удельную нагрузку, приходящуюся на единицу длины контактной линии как

.

(4.18)

В этом случае уравнение проверочного расчета будет иметь вид

.

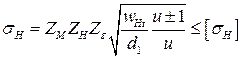(4.19)

Принимая в качестве проектного параметра межосевое расстояние и применяя подстановки: Т₂ = Т₁u, d₁ = 2a_w / (u ± 1) и b₂ = ψ_baa_w, где ψ_ba – коэффициент ширины венца колеса, получим из уравнения (4.14) стандартное выражение для определения межосевого расстояния передачи:

.

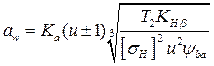(4.20)

где К_а = 49,5 – коэффициент.

Коэффициент ψ_ba и величину a_w согласуем со стандартными значениями этих параметров.

2. Расчёт на изгибную выносливость

В процессе работы зуб находится в сложном напряжённом состоянии. Согласно схеме, показанной на рисунке 4.4, зуб одновременно подвергается деформациям сжатия и изгиба. При этом наибольшие напряжения развиваются на левой (по схеме) растянутой стороне зуба.

Представим зуб как жестко защемленную консольную балку к вершине которой под углом α^´ приложено нормальное усилие F_n.

Рисунок 4.10 – Схема нагружения зуба

Перенесем по линии действия силу F_n на ось зуба и разложим на составляющую изгибающую зуб

,

(4.21)

и сжимающую зуб

.

(4.22)

Напряжение изгиба в опасном сечении зуба согласно эпюрам, изображенным на рисунке 4.4, находим по выражению

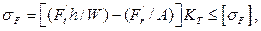
(4.23)

где W = b₂s²/6 – осевой момент сопротивления; A = b₂s – площадь опасного сечения.

Выразим величины h и s через модуль зацепления: h = μm и s = νm, где μ и ν - коэффициенты, учитывающие форму зуба. Тогда из выражения (4.23) получим:

.

(4.24)

Заменим выражение, входящее в скобку, коэффициентом Y_F – коэффициент формы зуба, величина которого зависит от числа зубьев. Тогда с учетом коэффициента нагрузки получим формулу проверочного расчета прямозубых передач:

(4.25)

где [σ_F] – допустимое напряжение изгиба.

Применяя подстановку: F_t = 2T₁ / d₁, d₁ = z₁m, b₂ = ψ_mm, получим

.

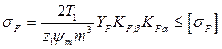(4.26)

Откуда требуемый модуль зацепления

.

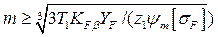(4.27)

Полученное значение согласуем со стандартным рядом.