Лекция № 12 (2 часа)

КОСОЗУБЫЕ ЦИЛИНДРИЧЕСКИЕ ПЕРЕДАЧИ

План лекции

1. Общие сведения

2. Расчет на контактную прочность.

3. Расчет на изгибную выносливость.

Общие сведения

В отличие от прямозубой передачи в косозубой передаче зубья расположены под углом β к образующей, оси колёс при этом остаются параллельными.

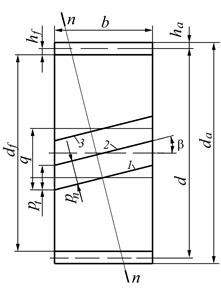
Рисунок 4.11 – Схема косозубого колеса

За счет наклонного расположения зубьев передаваемая нагрузка распределяется на несколько зубьев. На рисунке 4.11 показано расположение контактных линий 1, 2 и 3 в поле зацепления q. При этом пара 2 зацепляется по всей длине зубьев, а пары 1 и 3 – лишь частично. Это позволяет значительно увеличить длину контактной линии

,

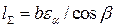(4.28)

где ε_α – коэффициент торцового перекрытия

,

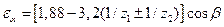(4.29)

где z₁ и z₂ – число зубьев шестерни и колеса; b – ширина колеса.

Также за счет наклонного расположения зубья входят в зацепление не сразу по всей длине как в прямозубой передаче, а постепенно.

В этой связи по сравнению с прямозубой передачей косозубая обладает следующими преимуществами:

- повышается нагрузочная способность;

- увеличивается плавность работы передачи;

- снижаются динамические нагрузки;

- уменьшается шум при работе;

- увеличиваются окружные скорости.

В отличие от прямозубой передачи косозубая характеризуется двумя шагами (рисунок 4.11) – нормальным p_n и окружным (торцовым) p_t; при этом p_t = p_n / cosβ. Соответственно шагам имеем два модуля– нормальный и окружной (торцовый):

; .

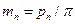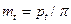(4.30)

При этом

.

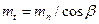(4.31)

Стандартным является нормальный модуль.

Диаметры делительной и начальной окружности

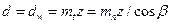
(4.32)

Диаметры вершин и впадин зубьев

. .

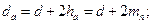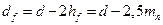(4.33)

В процессе работы в зацеплении косозубых колес развивается усилия, показанные на рисунке 4.12:

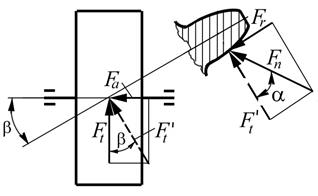
Рисунок 4.12 – Усилия в зацеплении косозубых колес

окружное усилие

; .

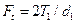(4.34)

осевое усилие

; .

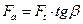(4.35)

радиальное усилие

; .

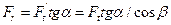(4.36)

нормальное усилие

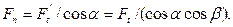
(4.37)

Наличие осевой составляющей F_a, которой дополнительно нагружаются опоры, является недостатком косозубых колёс. Угол β ограничен пределами 8 ÷ 20˚, так как с ростом этого угла увеличивается осевая нагрузка. В шевронных зубчатых колесах этот недостаток устраняется, так как осевые нагрузки равны и направлены навстречу друг к другу. В остальном шевронные и косозубые передачи аналогичны, за исключением угла β, который ограничен пределами в 25 ÷ 40˚.

Для нарезания прямых и косых зубьев используют один и тот же инструмент, поэтому профиль косого зуба в нормальном сечении n – n (рисунок 4.12) совпадает с профилем прямого зуба. Это позволяет теоретическим путем косозубое колесо заменить эквивалентным прямозубым с делительным диаметром

,

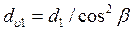(4.38)

и числом зубьев

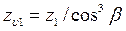
(4.39)

2. Расчёт на контактную прочность

Поскольку косозубое колесо может быть заменено эквивалентным прямозубым, то это позволяет использовать рассмотренную ранее методику расчета прямозубых колес на контактную прочность для расчета косозубых с учетом конструктивных особенностей этих колес. В основе этого расчета лежит формула Герца

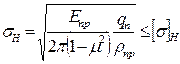
(4.40)

где Е_пр – приведенный модуль упругости материала колес; μ – коэффициент Пуассона; q_n – удельная нагрузка; ρ_пр – приведенный радиус кривизны боковой поверхности зубьев.

Удельная нагрузка с учетом формулы (4.28)

.

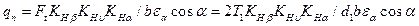(4.41)

По аналогии с прямозубыми колесами, выражая в формуле (4.10) значение d₁ через диаметр эквивалентного колеса d_v1 по выражению (4.38), получим

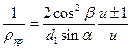
(4.42)

Сравнивая отношение q_n / ρ_пр для прямозубых и косозубых колес, находим

.

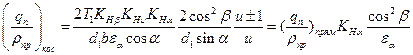(4.43)

Таким образом, указанные отношения отличаются друг от друга коэффициентом

.

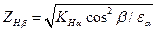(4.44)

Это коэффициент повышения прочности косозубых колес по контактным напряжениям по сравнению с прямозубыми. В соответствии с формулой (4.14)

.

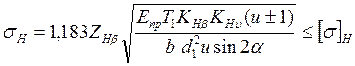(4.45)

При некоторых средних значениях β = 12⁰, ε_α = 1,5 и К_Нα = 1,1 получаем Z_Hβ = 0,85.

По аналогии с прямозубыми передачами из выражения (4.18) можно получить стандартное уравнение проверочного расчета для косозубых передач (ГОСТ 21354 – 87):

.

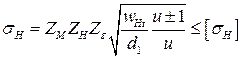(4.46)

где Z_M – коэффициент, учитывающий механические свойства материала сопряженных колес; Z_H – коэффициент, учитывающий форму сопряженных поверхностей зубьев; коэффициент, Z_ε – коэффициент, учитывающий суммарную длину контактных линий.

Последние два параметра определяют по выражениям:

,

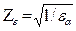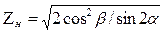
(4.47)

Принимая в качестве проектного параметра межосевое расстояние и применяя подстановки: Т₂ = Т₁u, d₁ = 2a_w / (u ± 1) и b₂ = ψ_baa_w, где ψ_ba – коэффициент ширины венца колеса, получим из уравнения (4.45) стандартное выражение (ГОСТ 21354 – 87):

.

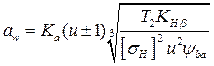(4.48)

где К_а = 43 – коэффициент.

Коэффициент ψ_ba и величину a_w согласуем со стандартными значениями этих параметров.