Цифровые измерительные приборы.

Основные требования, предъявляемые авиационной техникой и тех­нологией к средствам измерений, это высокая точность; быстродействие; возможность автоматизации процесса измерений; представление резуль­татов измерений в форме, удобной для обработки, в том числе при помощи ЭВМ; малые габариты и вес; высокая надёжность.

Статическая точность рассмотренных выше приборов может быть достаточно высокой; так, у некоторых видов электромеханических при­боров класс точности 0,05, а у компенсаторов и мостов – на порядок вы­ше. Но при реализации такой точности габариты приборов становятся большими. Это связано с тем, что глаз человека может обнаружить перемещение стрелки прибора относительно шкалы в пределах 0,2 мм, а разрешающая способность для приборов класса точности 0,05 долж­на быть не менее 2000, следовательно, длина шкала должна быть не менее 400 мм.

Наличие подвижных частей не позволяет получить высокие дина­мические качества и надёжность.

Разрешить проблему сочетания точности и быстродействия позво­лили цифровые приборы. Отсутствие в приборах подвижных частей поз­волило резко увеличить их надежность и долговечность. Представле­ние измерительной информации в цифровой форме дает возможность об­работки её в ЦВМ. Сравнительно легко осуществляется автоматизация процесса измерений.

Рассмотрим некоторые основные положения цифровой измеритель­ной техники.

Как уже отмечалось, под цифровым понимают такой измеритель­ный прибор, который автоматически вырабатывает дискретные сигналы измерительной информации, показания которого представлены в цифро­вой форме.

Под дискретным сигналом понимают сигнал, у которого информа­ция заложена не в размере величины, используемой для передачи этой информации, а в соответствующем ей количестве сигналов, их взаим­ном расположении и т.д., причем дискретный сигнал в отличие от неп­рерывного может иметь только определенное конечное число значений. Систему правил, используемую для представления инфор­мации посредством цифр и дискретных сигналов, называют кодом.

Под непрерывной величиной x(t) следует понимать величину, ко­торая может иметь в заданном диапазоне бесконечно большое число значений в определенном интервале времени при бесконечно большом числе моментов времени.

Под аналоговой величиной понимают некоторую вторичную величи­ну, все значения которой являются непрерывной функцией значений не­прерывной, (исходной) величины.

Цифровой сигнал – это частный случай дискретного сигнала, ког­да соответствующая ему информация представлена в виде цифр.

На рис. 2.21 (а, б, в, г) представлены соответственно непрерывная величина, квантованная по времени (дискретизированная) и непрерывная по уровню величина, непрерывная по времени и квантованная по уровню величина, и квантованная как по времени так и по уровню величина (цифровая).

Операцию перехода от непрерывной величины к квантованной на­зывают квантованием по уровню. Величину 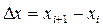, называют шагом квантования, величину 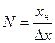– разрешающей способностью. X_н – диапазон изменения входной величины.

Возникающая при квантовании погрешность лежит в пределах ± 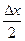и носит случайный характер с равномерным симметричным распределе­нием. Её среднее квадратическое значение

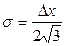. (2.78)

В процессе дискретизации (квантования по времени) возникают динамические погрешности

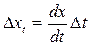, (2.79)

зависящие как от скорости изменения сигнала, так и от шага дискре­тизации.

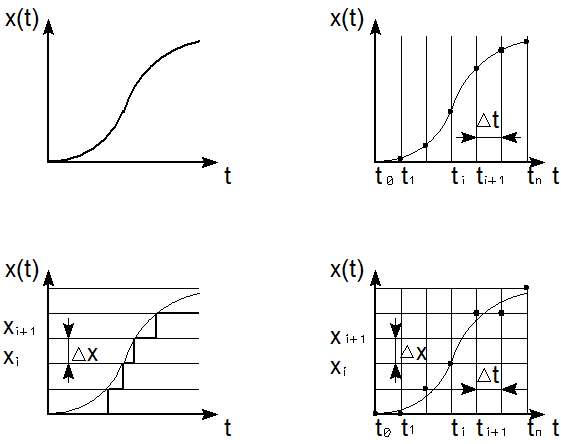
Рис. 2.21

В цифровых измерительных приборах происходит преобразование непрерывной физической величины в дискретную и квантованную величи­ну с последующей индикацией на цифровом отсчетном устройстве.

Процесс аналого-цифрового преобразования состоит из многократ­ного сравнения входного непрерывного сигнала с набо­ром сигналов, воспроизводимых мерами или сформированных с помощью мер.

Применение практически безынерционных элементов сравнения, как правило, электронных компараторов, позволяет очень быстро (на­носекунды) определить момент равенства неизвестной и сформирован­ной величин, что приводит к большому разнообразию алгоритмов фор­мирования уравновешивающей величины.

Наибольшее распространение на практике нашли три классичес­ких метода преобразования: последовательного счета, поразрядного уравновешивания, считывания.

При методе последовательного счёта входная непрерывная вели­чина уравновешивается суммой одинаковых и минимальных приращений-квантов, находящихся в известном соотношении с воспроизводимой ме­рой величиной. Результат преобразования характеризуется числом квантов, используемых при преобразовании. Число квантов представ­ляется в виде последовательного единичного кода и с помощью счетчи­ка преобразуется в позиционный код. Цифровые приборы, основанные на таком методе, применяются преимущественно для измерения интервалов времени, точнее, временных интервалов действия активных физических величин, частоты и других физических величин с промежуточным преоб­разованием их в интервал времени (или частоту). На рис. 2.22 пока­зана схема такого устройства. Измеряемый интервал времени т_х огра­ничивается моментами появления двух электрических импульсов – "на­чало" и "конец". По этим импульсам формирователь ФC вырабатывает строб-импульс длительностью т_х, который поступает на один из вхо­дов схемы совпадений И. На другой её вход подаются импульсы с час­тотой f₀ , вырабатываемые генератором опорных импульсов. Число им­пульсов, которое будет подсчитано счетчиком с_ч и зафиксировано отсчётным устройством ОУ будет равно

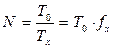
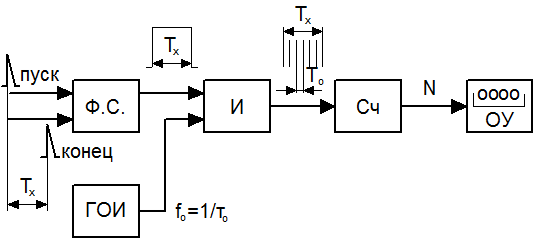
Рис.2.22

Из (2.78) видно, что погрешность измерения Т_x определяется погрешностью формирования опорной частоты f₀ . Применение в генераторах опорной частоты кварцевых резонаторов позволяет получить очень высокую стабильность частоты fо. Практически достижимые значения нестабильности частоты кварцевого резонатора 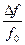лежат в пределах от 10^-6 до 10^-10 , следовательно, измерение временных ин­тервалов возможно с такой же погрешностью.

Такие устройства очень широко применяются для измерения рас­стояний до объектов и высоты полета летательных аппаратов радиотех­ническими методами, при измерениях расхода топлива ультразвуковыми методами, при измерении напряжений, токов, сопротивлений и других физических величин, преобразуемых во временные интервалы.

Если вместо т_х (на рис. 2.22) сформировать образцовый времен­ной интервал Т₀ , а на второй вход схемы совпадений подать сигнал измеряемой частоты , то уравнение (2.78) можно записать как

,

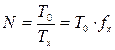из которого видно, что можно измерять частоту f_x с погрешностью, определяемой погрешностью формирования интервала Т₀ . Формирование Т₀можно осуществить при помощи кварцевых резонаторов и делителей частоты с очень малой погрешностью. Применив дополнительные преоб­разователи различных физических величин в частоту следования элект­рических импульсов, можно измерять скорость полета самолета, высоту полета, скорости вращения валов двигателя, напряжения, токи, сопротивления и многие другие.

При методе поразрядного уравновешивания входная величина срав­нивается с другой однородной величиной, получаемой в результате суммирования различных по величине приращений. Сумма приращений компенсирующей величины (с погрешностью до наименьшего приращения) принимается за числовое значение измеряемой величины. Обычно набор приращений соответствует выбранному цифровому коду.

Принцип поразрядного уравновешивания используется главным об­разом в цифровых приборах для измерения электрических величин, та­ких как напряжение, ток, сопротивление, и величин, преобразуемых в электрические.

Если автоматизировать рассмотренные ранее компенсаторы и изме­рительные мосты с дискретным уравновешиванием, то получим характер­ные примеры приборов поразрядного уравновешивания.

Структурная схема цифрового вольтметра поразрядного уравновшивания показана на рис.2.23.

Рис.2.23

Компенсирующее напряжение U_k формируется формирователем компенсирующего напряжения ФКН, управляемого программным запоминающим устройством ПрЗу. Алгоритмы формирования U_k многочисленны и многообразны, а принцип уравновешивания активных электрических величин сохраняется.

Метод считывания состоит в том, что в "памяти" кодирующего устройства цифрового прибора имеется набор всех возможных для даннoгo прибора кодов и соответствующих им компенсирующих активных величин, каждая из которых подается на вход одного из элементов сравнения. Число элементов сравнения равно числу компенсирующих величин. На вторые входы всех элементов сравнения подаётся измеряемая величина. Результат преобразования (измерения) фиксируется по числу сравнивающих устройств, отметивших равенство или превыше­ние входной величины по отношению к каждому из компенсирующих. Не­посредственным результатом преобразования является параллельный единичный код в виде сигналов на выходах сравнивающих устройств. На рис. 2.24 изображена схема цифрового вольтметра, основанного на принципе считывания.

Рис.2.24

Компенсирующие напряжения формируются делителями напряжения, на входы которых подано образцовое напряжение U₀ , формируемое при помощи мер напряжения. Сигналы с элементов сравнения расшифровы­ваются дешифратором ДШ и подаются на отсчётное устройство.

Преобразователи считывания находят широкое распространение из-за того, что они в принципе обладают самым высоким быстродей­ствием из всех видов преобразователей напряжения в код. Недостат­ком их является большой объём оборудования, что приводит к сниже­нию надёжности и увеличению стоимости. В связи с успехами интегральной технологии недос­татки можно устранить и считать метод весьма перспективным.

Погрешности цифровых приборов определяются точностью и ста­бильностью мер и измерительных преобразователей, переходными соп­ротивлениями коммутирующих элементов, дрейфом нуля элементов сра­внения и погрешностью квантования.

С целью улучшения метрологических характеристик и расширения возможностей цифровых измерительных приборов их снабжают встроен­ными микропроцессорными устройствами.