Динамические свойства измерительных преобразователей и приборов.

Энергия, поступающая на вход ИП или прибора, может преобразо­вываться из одного вида в другой, накапливаться, расходоваться и перераспределяться между элементами устройств, такими как подвиж­ные части, характеризуемые массой и моментом инерции, пружины, индуктивные элементы, ёмкости. При наличии таких элементов в сред­ствах измерений возникают переходные процессы при любом изменении входной величины, что является причиной появления динамических погрешностей. Следовательно, ИП или прибор представляют динами­ческую систему, которая описывается дифференциальным уравнением соответствующего порядка. Динамические свойства приборов определяются в результате решения этих уравнений. Кроме дифференциаль­ных уравнений, динамические характеристики определяют: передаточ­ная функция, частотные амплитудно-фазовые характеристики, переход­ная и импульсная функции.

Подробно динамические свойства приборов, как систем автоматического управления, рассматриваются в дисциплине «Теория автомати­ческого управления» , но не рассматриваются некоторые важные аспек­ты, касающиеся применения некоторых динамических свойств для целей
измерения, анализа динамических погрешностей и связи их со статическими погрешностями.

Большинство звеньев ИП и приборов могут быть описаны диффе­ренциальными уравнениями первого или второго порядков. Более высо­кие порядки уравнений получаются, как правило, в результате ком­бинаций звеньев первого и второго порядков. Так, например, рас­смотренные выше приборы с уравновешиванием обобщенных сил описы­ваются дифференциальным уравнением второго порядка

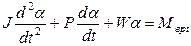(2.42)

где J – момент инерции подвижной части приборов; P – коэффици­ент успокоения (демпфирования): W – удельный противодействующий момент; a – угол отклонения; М_врt – мгновенное значение вращающе­го момента. Момент инерции определяется массой и геометрией под­вижкой части ИП, удельный противодействующий момент – упругими свойствами пружин, растяжек или подвесов, а коэффициент успокоения определяется трением подвижной части о воздух и вводитcя искусственно при помощи специальных устройств – успокоителей или демпферов. Он оказывает влияние только на динамические характеристики, не искажая статических.

Запишем уравнение (2.42) в виде

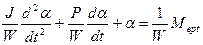(2.43)

которое при tॠпримет вид (переходные процессы закончатся, а скорость и ускорение станут равными нулю)

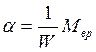(2.44)

т.е. получим статическое уравнение ИП – частное решение дифферен­циального уравнения.

Динамические свойства собственно преобразователя определяют­ся коэффициентами его левой части. Найдем общее решение уравнения (2.43), для чего составим его характеристическое уравнение

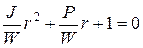(2.45)

и найдем его корни

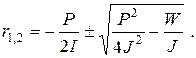(2.46)

Если колебательная система, не имеет потерь (Р =0), то величина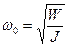

определяет резонансную угловую частоту колебаний системы.

Вынесем за скобки величину w₀ в уравнении (2.45)

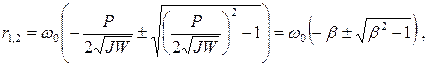(2.47)

где 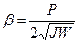– степень успокоения (степень демпфирования, от­носительный коэффициент затухания), определяющая потери энергии. В зависимости от значения степени успокоения различают три режима движения:

1) при b<1корни характеристического уравнения комплексные сопряженные, что свидетельствует о колебательности движения;

2) при b>1 оба корня вещественные и разные, следовательно, движение апериодическое;

3)при b=1 оба корня вещественные и равные, что соответст­вует граничному случаю, представляющему для практики особый инте­рес.

При критическом успокоении подкоренное выражение уравнения (2,46) равно нулю

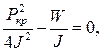(2.48)

откуда найдем, что

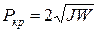. (2.49)

Из (2.49) видно, что критический коэффициент успокоения определяется параметрами элементов системы, способными к. накопле­нию энергии. Как правило, эта величина для конкретного прибора фиксирована и связана со статическими характеристиками ИП.

Изменение степени успокоения b=Р/Р_кр с целью получения не­обходимого режима движения осуществляется изменением коэффициента успокоения Р, который, как следует из (2.42), является коэффици­ентом при скорости. От него зависит значение момента успокоения

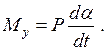(2.50)

Для создания М_у применяют процессы с рассеиванием энергии, например, при движении твердых тел в газообразных и жидких средах (воздушные и жидкостные успокоители), при движении короткозамкнутых контуров в магнитном поле (индукционные успокоители).

Одна из важных динамических характеристик измерительных при­боров – время установления показаний t_y – тесным образом связана со степенью успокоения bи периодом собственных колебаний системы

.

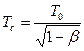Если зададим динамическую погрешность равной 1%, то время, за которое выходная величина достигнет уровня 0,99a_уст , называют временем установления показаний (временем успокоения).

При b<1 время успокоения может быть оценено по эксперимен­тально полученной зависимости

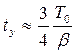(2.51)

а при b>1 по формуле

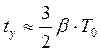(2.52)

Установлено, что наиболее выгодное с точки зрения быстро­действия значение bравно 0,7-0,9.

Следовательно, для увеличения быстродействия необходимо уменьшать период собственных колебаний системы (или увеличивать частоту), что может быть достигнуто (2.46) уменьшением момента инерции (обобщенной массы) или увеличением удельного противодейст­вующего момента,

Но такие мероприятия, как видно, например, из уравнения (2.19), приводят к уменьшению чувствительности ИП, причем умень­шение чувствительности происходит интенсивнее, чем уменьшение пе­риода собственных колебаний. Кроме того, уменьшается запас энер­гии в системе (энергоемкость системы), что приводит к уменьшению помехоустойчивости.

Из сказанного можно сделать следующие выводы:

I) статические и динамические характеристики ИП и приборов связаны между собой. Улучшение динамических характеристик, как правило, приводит к ухудшению статических, т.е., возможен своеоб­разный обмен качеством;

2) для улучшения статических характеристик и помехозащищен­ности необходимо увеличивать энергоёмкость системы;

3) для улучшения динамических свойств ИП необходимо умень­шать энергоемкость системы.

Возникающие противоречия разрешаются конструктором при разра­ботке конкретного прибора с учетом условий его применения.

Если все конструкторские приемы исчерпаны, а статические и динамические характеристики всё равно не удовлетворяют требовани­ям технического задания на разработку устройства, то в него допол­нительно вводят корректирующие элементы, способствующие уменьше­нию периода собственных колебаний системы, или усилители, позво­ляющие, увеличить энергоёмкость системы.

Очень важными для анализа средств измерений являются амплитудно- фазочастотные характеристики.

Для ИП, описываемых дифференциальными уравнениями второго порядка, они имеют вид

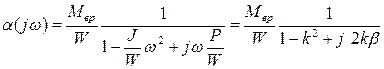, (2.53)

где w – текущая угловая частота; k = w/w₀ – относительная час­тота.

Отсюда амплитудно-частотная характеристика

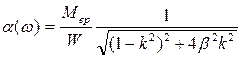, (2.54)

а фазочастотная

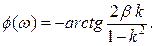(2.55)

На рис. 2.4 приведено семейство кривых, соответствующих уравнению

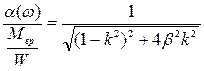. (2.56)

Анализируя полученные зависимости, можно сделать следующие выводы:

1) чувствительность преобразователей уменьшается с возраста­нием частоты w, что свидетельствует о фильтрующих свойствах ИП и приборов, описываемых дифференциальными уравнениями второго (как и других) порядка, причем характеристики фильтра могут бить изменены путем изменения величин W, J, P, b.

2) ИП и приборы, имеющие приведенные характеристики, могут быть использованы для коррекции динамических характеристик дру­гих ИП, находящихся в одной с ними измерительной цепи;

3) резкое возрастание чувствительности на резонансной час­тоте при малых значениях степени успокоения используется при разработке высокочувствительных селективных устройств сравнения пере­менного тока – вибрационных гальванометров;

4) при степени успокоения b = 0,6¸0,8 имеется участок с постоянной чувствительностью в диапазоне частот, примерно равном (0¸0,4) w₀, что широко используется при разработке вибраторов (гальванометров) электромеханических осциллографов, предназначен­ных для записи различных величин, изменяющихся во времени.

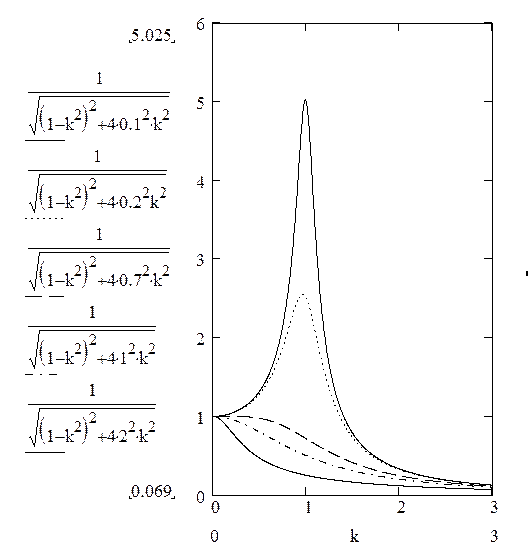
Рис. 2.4

График, характеризующий частотную погрешность, будет выгля­деть аналогично изображенному на рис. 2. 4, с той лишь разницей, что ось абсцисс будет сдвинута вверх на единицу.

Важнейшей динамической характеристикой ИП и приборов являет­ся передаточная функция, которая для рассматриваемых систем второ­го порядка равна

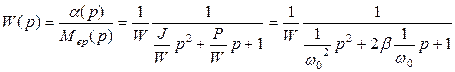. (2.57)

Достаточно подробно такие передаточные функции исследуются в теории автоматического управления.

Анализ передаточной функции приводит к выводам, сделанным выше при исследовании переходной функции и амплитудно-фазочастотных характеристик, что вполне естественно, поскольку имеем дело с различными формами представления одного и того же процесса.

Рассмотрим два особых случая применения динамических харак­теристик в измерительных цепях.

Если электромеханический ИП выполнить таким образом, чтобы момент инерции был большим, а коэффициент успокоения малым, то уравнение (2.67) можно записать как

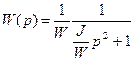, (2.58)

т.е. получим колебательное звено с медленно затухающей амплитудой колебаний. Известна связь амплитуды колебания такой системы и энергии, поступившей в нее в виде короткого импульса (t_и£0.1Т₀)

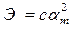(2.59)

где с - коэффициент, зависящий от параметров системы. Указанное свойство используют при разработке баллистических гальванометров, применяемых, например, при магнитных измерениях. Основной недос­таток баллистического гальванометра – необходимость получения ко­ротких импульсов напряжения или тока, подаваемых на его вход.

Если ИПвыполнить с очень малым удельным противодействующим моментом, закрепив подвижную часть при помощи без моментных растя­жек или подвесов, то получим

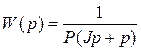. (2.60)

Введём дополнительное условие: малый момент инерции и боль­шой коэффициент успокоения (успокоители обычно индукционные), тогда с некоторой погрешностью: уравнение (2.60) можно записать
как

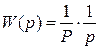(2.61)

т.е. получим интегрирующее звено с коэффициентом усиления 1/P.

Такие преобразователи хорошо согласуются с дифференцирующи­ми ИП, например, с измерительными катушками, предназначенными для измерения магнитного потока Ф индукционным методом. Передаточная функция их

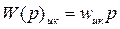, (2.62)

где 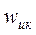– число витков измерительной катушки.

Соединив последовательно оба звена, получим безынерционное звено. Следовательно, имеется возможность непрерывного преобразова­ния магнитного потока в перемещение. Приборы такого типа называют веберметрами. Они широко распространены в технике магнитных изме­рений.