Методы получения дискретного аналога

Теоретические основы математического моделирования

Основные уравнения

С точки зрения физики потоков все вентиляционные течения можно разделить на три класса в зависимости от соотношения сил тяжести и инерции в потоке жидкости, т. е. в зависимости от значения числа Ричардсона течения:

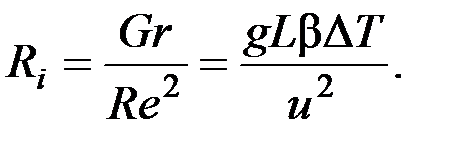
Так, если R_i<<1, то в течении преобладает вынужденная конвекция. К таким задачам относятся течения в каналах, воздуховодах, вентиляция изотермичными струями и т. д.

Если R_i>>1, то течение обусловлено в основном естественно-конвектививными потоками, например восходящий поток над нагретым источником, вытесняющая вентиляция.

Наиболее сложными для описания являются смешанно–конвективные течения (т. е. течений с одновременным действием свободно-конвективных и вынужденных сил). Для таких течений число R_i≈1. Это имеет место для большого числа вентиляционных течений, где сосредоточенная подача воздуха соседствует со свободно-конвективными струями, поднимающимися от человека, оборудования и т. д. А также, например, при совместном использовании вытесняющей и перемешивающей вентиляции, что характерно для таких объектов как театры, стадионы и т. д.

Развитие вычислительных методов, вычислительных ресурсов (кластеров, суперкомпьютеров) позволило находить частные решения для любого класса вентиляционных течений, в том числе и теоретически плохо изученных смешанных течений.

Поведение существенно неизотермичных течений описывается системой дифференциальных уравнений относительно осредненных [1] параметров потока:

уравнение сохранения массы

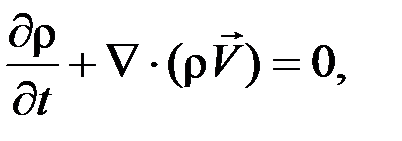(1)

уравнение сохранение импульса

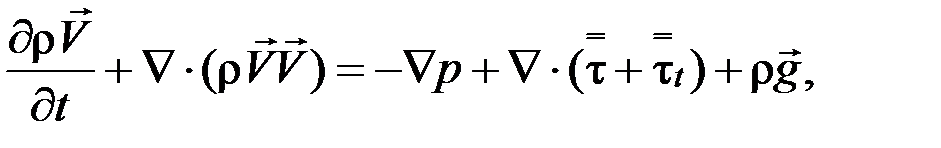(2)

где t – время, V – вектор скорости, p – пьезометрическое давление, ρ – плотность.

Тензор вязких напряжений 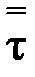, определен с помощью реологического закона Ньютона

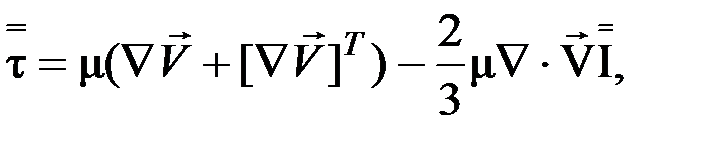(3)

а тензор турбулентных напряжений 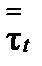– в соответствии с обобщенной гипотезой Буссинеска

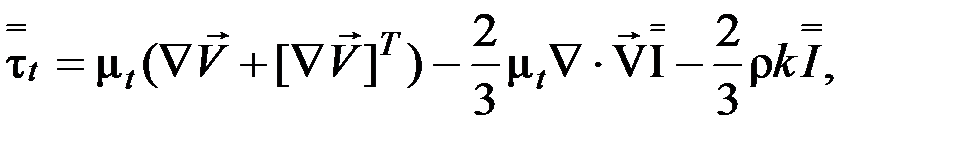(4)

уравнение состояния ,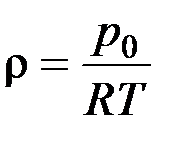

уравнение сохранения энергии

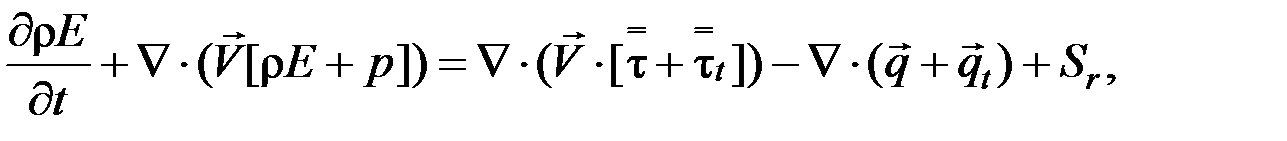(5)

молекулярная составляющая вектора плотности теплового потока

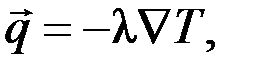(6)

турбулентная составляющая вектора плотности теплового потока

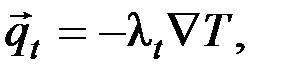(7)

турбулентная теплопроводность определяется как

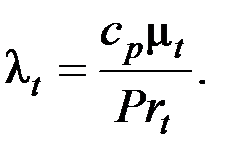(8)

Для получения информации о полях концентрации вредных веществ, пара система дополняется уравнением сохранения массы для компоненты газа:

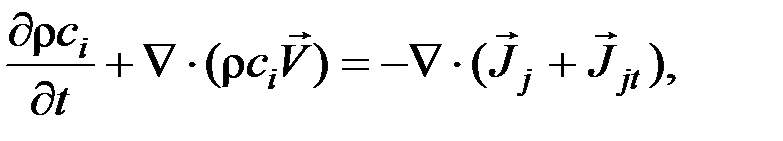(9)

диффузионный поток компоненты

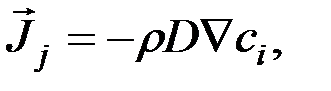(10)

турбулентный поток массы компоненты

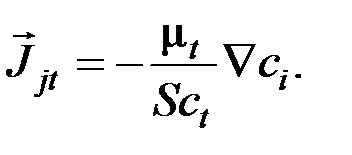(11)

При расчете смеси в уравнении переноса энергии (5) молекулярную и турбулентную составляющие вектора плотности теплового потока следует рассчитывать с учетом переноса тепла компонентой:

молекулярная составляющая вектора плотности теплового потока

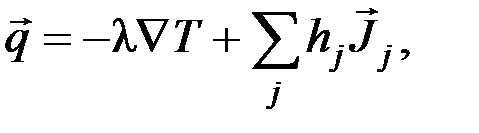(12)

турбулентная составляющая вектора плотности теплового потока

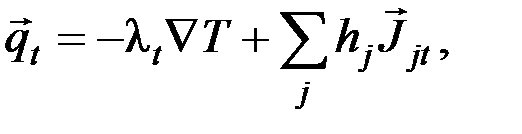(13)

а в уравнениях сохранения плотность следует трактовать как плотность смеси (например воздух +водяной пар).

Для нахождения характеристик турбулентности необходимо использование той или иной модели турбулентности, например k-ε:

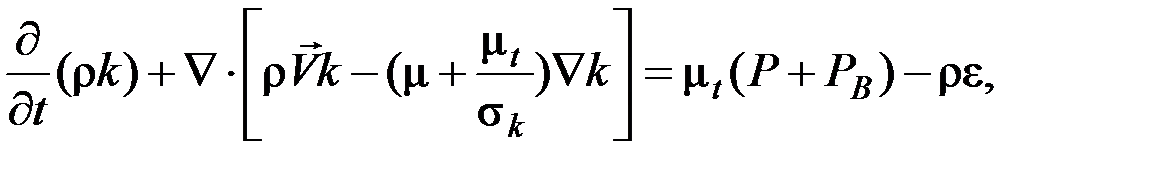(14)

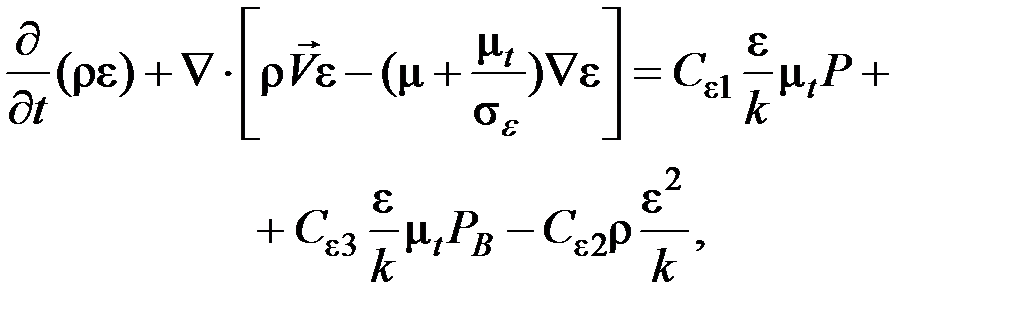(15)

генерационный член в уравнениях переноса (12) и (13)

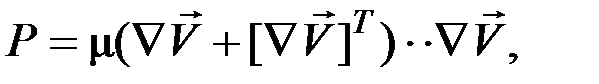(16)

P_B – дополнительный генерационный член, учитывающий влияние сил плавучести на характеристики турбулентности

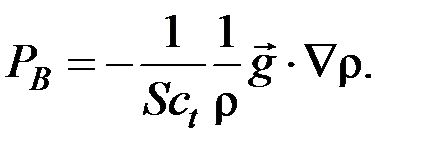(17)

Приведенная формулировка k-e модели является высокорейнольдсовой. Поэтому для постановки граничный условий на стенке должны использоваться так называемые стеночные функции, базирующиеся на предположении, что профиль скорости в пристенном турбулентном пограничном слое имеет линейный и логарифмический участки:

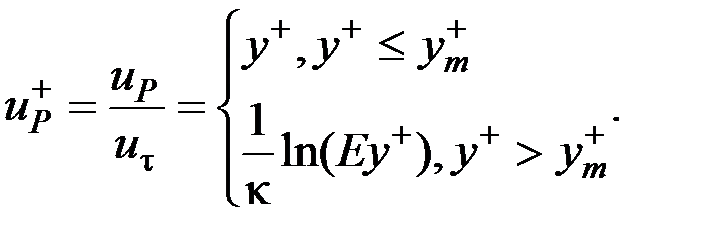
Значение диссипации кинетической энергии турбулентности ε в пристенной ячейке определяется из условия локального равновесия (равенство генерации и диссипации турбулентности)в пристенной ячейки:

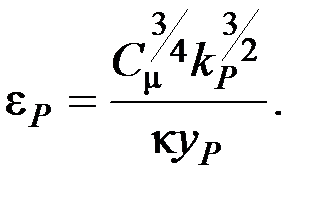
Что касается уравнения для переноса k, то оно решается вплоть до стенки с использованием граничного условия

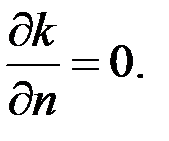
Для помещений, в которых присутствуют существенные теплопритоки от освещения, массива зрителей, оборудования пренебрежение раздельного учета лучистой составляющей тепловых потоков может привести к искажению прогнозируемого поля температуры, циркуляции воздуха в помещении, картины течения во всем объеме.

В связи с этим для расчета такого типа течений систему уравнений (1)-(17) необходимо дополнить уравнениями радиационного теплообмена [2]:

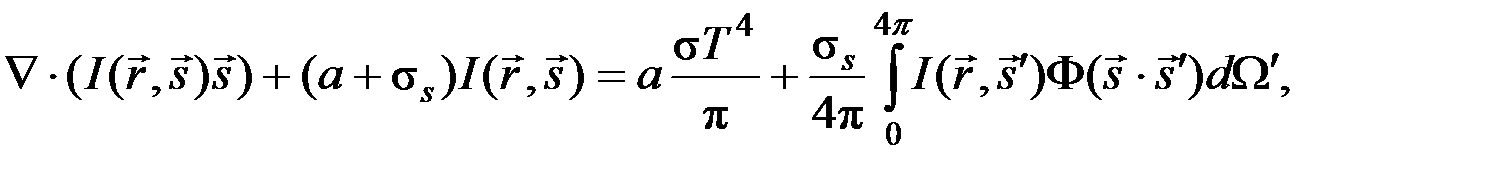(18)

где 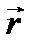– радиус-вектор, 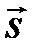– вектор направления излучения, 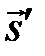– вектор рассеяния, a – коэффициент поглощения, σ_s – коэффициент рассеяния, I – полная интенсивность излучения, зависящая от радиус-вектора и направления излучения, Φ – фазовая функция, определяющая диаграмму рассеяния, Ω′ – телесный угол, σ – постоянная Стефана -Больцмана 5,67×10^-8 W/(m²×K⁴).

Методы получения дискретного аналога

Для решения уравнений Рейнольдса используют численные методы [3, 4, 5, 6, 7], выбор которых зависит от решаемой задачи.

Смысл численного решения дифференциального уравнения состоит в том, чтобы получить значения искомой переменной в рассматриваемом пространстве. В численном методе рассматриваются значения переменных в конечном числе точек расчетной области. Метод дискретизации сводится к получению системы алгебраических уравнений, которые являются дискретными аналогами исходных дифференциальных уравнений. При этом предполагается, что при достаточно мелкой сетке, решение дискретных уравнений является хорошим приближением к точному решению исходных дифференциальных уравнений. Дискретизация дифференциальных уравнений может быть выполнена разными методами, при этом используемая схема должна быть устойчивой и сходящейся.

В общем случае процедура решения задачи сводится к следующим этапам:

1. Выполняется дискретизация дифференциальных уравнений, т. е. переход к алгебраическим уравнениям относительно искомых переменных (скорости, давления, температуры и т. п.) в конечном числе точек в пределах расчетной области.

2. Производится решение алгебраических уравнений.

В настоящее время наиболее распространены следующие методы решения уравнений Рейнольдса:

· конечных разностей;

· контрольного объема:

· конечных элементов.

В последнее время приоритет отдается методу контрольного объема, который подробно рассмотрен в работе [4].