Метод контрольного объема

Преимущество этого метода заключается в том, что в его основе лежат законы сохранения. Поэтому, в отличие от метода конечных разностей, метод контрольного объема обеспечивает консервативность численной схемы, что позволяет даже на относительно грубых сетках получать приемлемые по точности решения [4, 8].

Основная идея метода достаточно проста и легко поддается физической интерпретации. При дискретизации уравнений Навье-Стокса, осредненных по Рейнольдсу, расчетная область разбивается на большое количество непересекающихся элементарных объемов, таким образом, чтобы каждый объем содержал только одну расчетную (узловую) точку. Совокупность элементарных объемов называется расчетной сеткой. Ячейки сетки могут иметь различную форму. Наиболее часто используются шестигранники (гексаэдры) и четырехгранники (тетраэдры). Метод контрольного объема позволяет использовать ячейки с произвольным числом граней (пирамиды, призмы, сложные многогранники и т. п.).

Решение системы уравнений (1)–(18) представляется в виде набора значений искомых параметров в центрах этих объемов. Например, если разбить объем помещения на 1000 отдельных элементарных объемов (ячеек), то в результате решения мы будем иметь 1000 значений температуры, скорости, давления и т. д. На рис. 2 представлен фрагмент расчетной области. Ячейки пронумерованы индексами i, j, k.

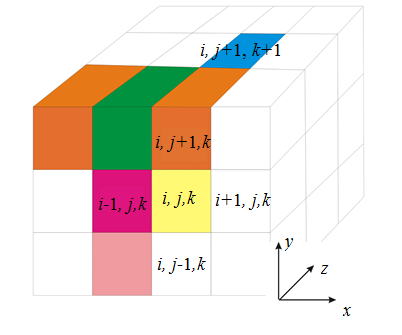
Рис. 2. Фрагмент расчетной области

Интегрирование дифференциальных уравнений производится по каждому элементарному объему. Интегралы вычисляются с использованием интерполяционных формул, при помощи которых определяют значения искомых переменных между расчетными точками. В результате получают дискретный аналог исходных уравнений в узловых точках, который отражает закон сохранения изучаемых переменных в каждом конечном объеме.

Следует отметить, что в большинстве современных расчетных гидродинамических пакетах таких как «STAR-CD», «FLUENT», «CFX» и многих других для дискретизации уравнений модели реализован метод контрольного объема.

Расчетные сетки

Процесс построения сетки относится к ключевым моментам проведения численного эксперимента. Выбор и построение адекватной для рассматриваемой задачи расчетной сетки является достаточно сложной и трудоемкой процедурой. Рациональный выбор сетки может значительно упростить численное решение задачи.

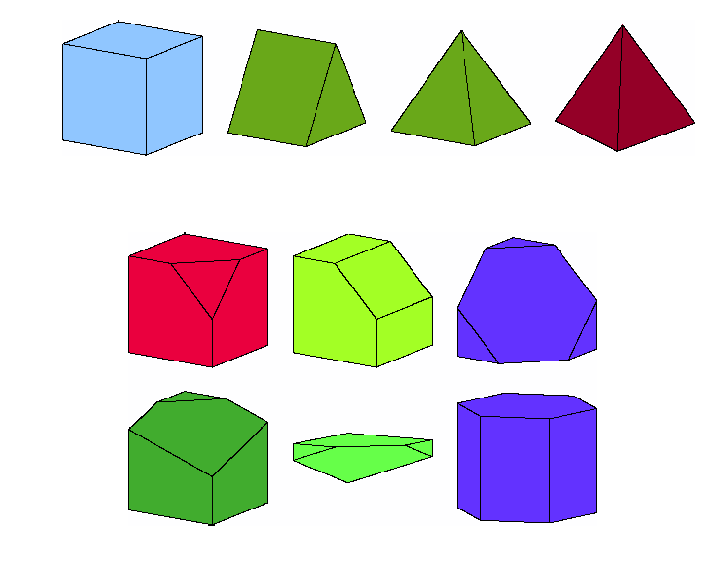
Рис. 3. Конфигурации ячеек сеток

Ячейки сетки могут иметь разную форму (рис. 3) и размеры, наилучшим образом подходящие для решения конкретной задачи. Наиболее простой вид сетки, когда ячейки одинаковы и имеют кубическую форму.

Как правило, вблизи твердых поверхностей сетка сгущается, т. е. ячейки имеют меньший размер по нормали к поверхности. Это делается для повышения точности расчетов в тех областях, где градиенты потоков изучаемых параметров изменяются быстрее, например, в пограничном слое.

Повысить точность расчетов и уменьшить ошибку аппроксимации можно 2 способами:

· повышением порядка точности дискретизации;

· уменьшением шага по сетке .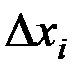

При решении нестационарных задач размеры ячеек Δx и шаг интегрирования по времени Δt связанны условием КФЛ (Куранта-Фридрихса-Леви): 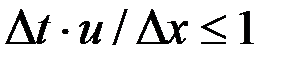, u – скорость.

Универсальные вычислительные программы, применяемые в настоящее время в инженерной практике, позволяют работать на произвольных неструктурированных сетках с использованием сильно скошенных элементов. При этом порядок точности дискретизации, как правило, не превышает второго. Для получения качественного решения необходимо строить расчетные сетки с малым шагом.

В пакете STAR-CCM осуществлен переход на использование полиэдральных ячеек (похожих на футбольный мяч), что позволяет за счет объединения ячеек исключить появление сильно скошенных ячеек.

Основное преимущество неструктурированных сеток по сравнению с регулярными – заключается в большей гибкости при дискретизации физической области сложной формы. При этом ячейки сетки должны иметь соизмеримые объемы или площади и не должны пересекаться. Однако к недостаткам такого типа сеток относится увеличение размерности сетки. Как показывает практика, для одного и того же объекта неструктурированная сетка при ее правильном построении имеет примерно в два раза больше ячеек, чем структурированная, что естественно приводит к увеличению времени счета по отношению к регулярным сеткам. Однако во многих случаях неструктурированные сетки являются единственно возможным вариантом построения из-за сложности геометрии объекта. Кроме того, при рациональном выборе алгоритма построения сетки время, затрачиваемое на построение неструктурированной сетки, оказывается существенно меньше, чем время построения структурированной (блочно-структурированной) сетки. В результате суммарное время, затраченное на решение задачи (включая время построения сетки и время счета), может при использовании неструктурированных сеток оказаться намного меньше, чем в случае структурированных.

Определение требуемой размерности сетки, само по себе, является весьма сложной задачей. Универсальный способ, которым следует руководствоваться при выборе размерности сетки, сводится к тому, что получаемое решение не должно изменяться при увеличении количества ячеек (сеточная сходимость).

Для типовых задач проведение исследования сеточной сходимости не является обязательным, так как можно ориентироваться на полученные ранее результаты. При переходе к изучению нового типа задач следует в обязательном порядке выполнить исследование сеточной сходимости и определелить требования к расчетной сетке.

Отметим, что при решении реальных задач вентиляции и кондиционирования воздуха характерное количество ячеек составляет, как правило, от 500 тысяч до 3 – 4 млн. в зависимости от геометрической сложности объекта, набора искомых параметров и специфики задачи. При этом время счета на кластере, состоящем, например из 24 ядер, может доходить до недели, а при решении нестационарных задач – до нескольких недель.

Пакет STAR-CCM+ включает в себя модуль для построения расчетных сеток. Существуют также отдельные пакеты для построения сеток, например, широко используемая – ANSYS, ICEM CFD (ICEM). Построенные во внешних пакетах сетки могут быть импортированы в пакет STAR-CCM+.