Метод конечных разностей

Одним из общеизвестных и наиболее простых методов получения конечно-разностных уравнений является разложение искомой функции в ряд Тейлора в окрестности точки x_i (рис. 1):

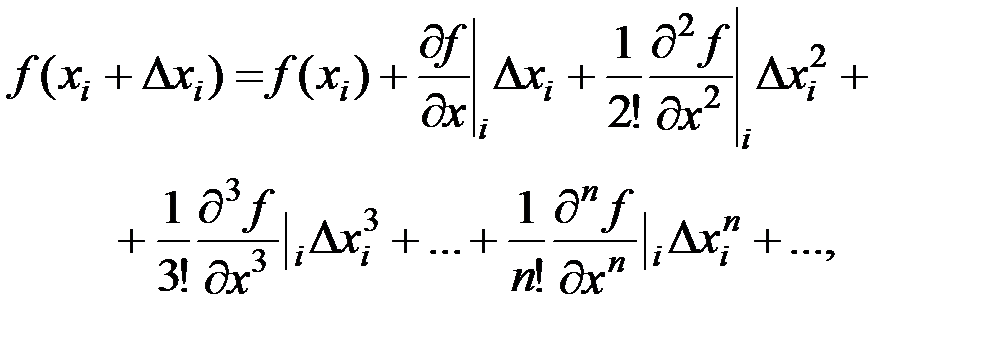(19)

где .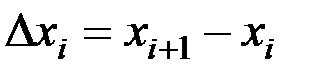

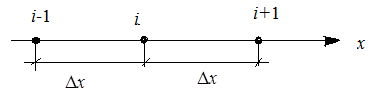
Рис. 1. Схема, поясняющая получение дискретного аналога

Данный ряд может быть оборван после любого числа членов, причем возникающая в результате ошибка (ошибка аппроксимации) определяется в основном следующим членом разложения, т. е. величиной 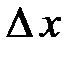(расстоянием между соседними ячейками), например

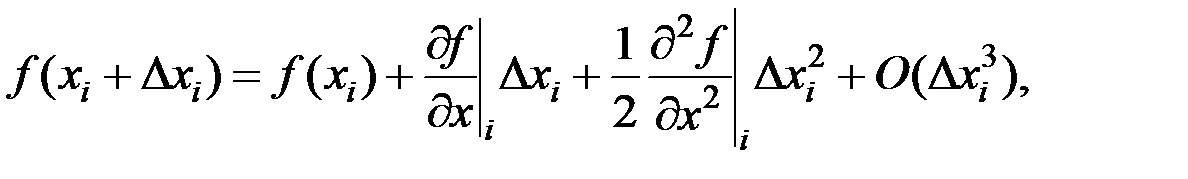(20)

где 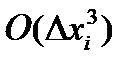– остаточный член, указывает на то, что точность аппроксимации соответствует точности 3-го порядка.

Ошибка аппроксимации будет быстро уменьшаться с уменьшением 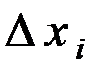. Дискретизация производных может быть выполнена с разным порядком точности.

Если отбросить третий член ряда, то

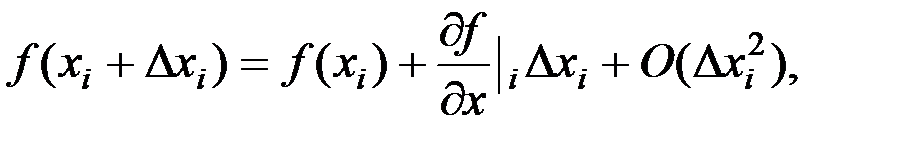
откуда после перегруппировки слагаемых получим дискретный аналог первой производной первого порядка точности

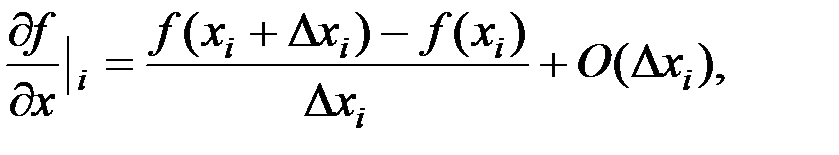
или

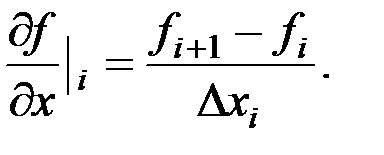. (21)

Центрально-разностная аппроксимация в точке x_i получается как разность разложений функции в ряд Тейлора в точках x_{i +1} и x_{i –1} относительно рассматриваемой точки x_i,

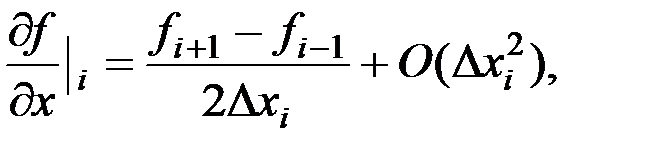(22)

которая имеет второй порядок точности.

Аналогично, центрально-разностная аппроксимация второй производной со вторым порядком точности может быть получена, если оставить первые три члена разложения ряда Тейлора,

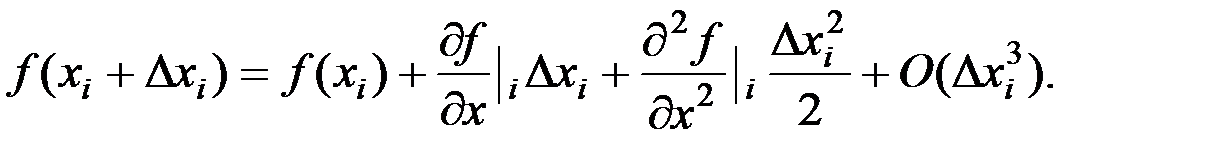(23)

Осуществляя перегруппировку, окончательно находим:

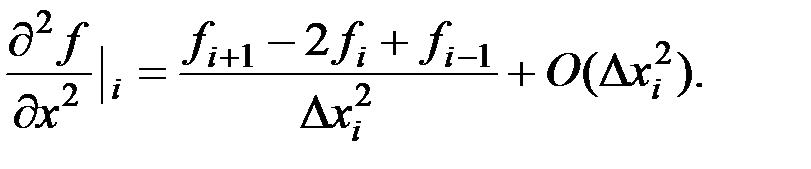(24)

Отметим, что при подстановке в уравнения сохранения (1)–(18) дискретных аналогов производных ошибка 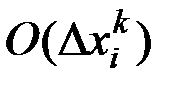, также попадает в уравнение, где k – точность порядка аппроксимации.

Данный метод получения дискретных аналогов производных достаточно прост. Однако при его применении к уравнениям (1)–(18) может нарушиться принцип консервативности, который заключается в том, что законы сохранения должны выполняться не только в целом для всей расчетной области, но и для любого внутреннего объема. В этом случае для получения правильного решения могут потребоваться слишком мелкие сетки, что при решении инженерных задач может оказаться достаточно сложным.