По таблице приложения для данного числа степеней находим

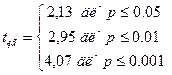
Строим ось значимости

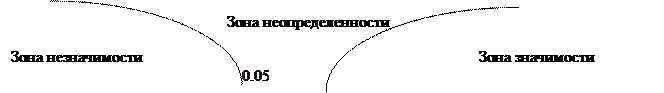
Т.о. обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,1% уровне или иначе говоря средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше чем в группе людей активно не занимающихся спортом.

В терминах статистических гипотез это утверждение звучит так : гипотеза Н0 о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза Н1 – о различии между экспериментальной и контрольной группой.

Двухвыборочный t-критерий для зависимых(связанных) выборок

Под связанными выборками понимаются наблюдения для одной группы объектов, причем все наблюдения попарно связаны с каждый объектом исследования и характеризуют его состояние до воздействия и после воздействия некоторого фактора.

Гипотезы

: среднее значение в выборке не отличается от нуля.

: среднее значение в выборке отличается от нуля.

Данные в выборке измерены по шкале интервалов или по шкале отношений Сравниваемые данные должны иметь нормальный закон распределения Сравниваемых выборок две для оной группы объектов наблюдения, причем имеет место парность наблюдений в выборках.

1. Предварительно проверяется нормальность закона распределения по одному из критериев согласия.

2. Рассчитывается (i=1..n) – попарные разности вариант, и 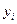результаты измерений для i-го объекта до и после воздействия некоторого фактора. Величину будем считать независимой для разных объектов и нормально распределенной

3. Рассчитываются (лучше в табличной форме): сумма попарных разностей и вспомогательные параметры и .

4. Рассчитывается 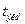- эмпирическое значение критерия степенями свободы по формуле

Где n – численность выборки.

5.Найденное эмпирическое значение 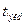критерия Стьюдента сравнивается с критическим значением 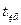(по таблице 1 приложения) для данного числа степеней свободы.

Нулевая гипотеза при заданном уровне значимости принимается, если эмпирическое значение .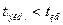

Критическое значение для выбранной вероятности и заданного числа степеней свободы можно найти по встроенной в Excel функции СТЬЮДРАСПОБР.

Пример.

Психолог предположил, что в результате тренировки, время решения эквивалентных задач (т.е. имеющих один и тот же алгоритм решения ) будет значительно уменьшаться. Для проверки гипотезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задачи.

Решение задачи представим в таблице.

Номер испытуемого	1 задача	3 задача
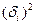
	4,0	3,0
	3,5	3,0	0,5	0,25
	4,1	3,8	0,3	0,09
	5,5	2,1	3,4	11,56
	4,6	4,9	-0,3	0,09
	6,0	5,3	0,7	0,49
	5,1	3,1	2,0
	4,3		1,6	2,56
Суммы	37,1	27,9	9,2	20,04

Число степеней свободы =8-1=7. По таблице Приложения находим

123

Дата добавления: 2016-04-06; просмотров: 1066;