Строим ось значимости



|


Т.о. на 5% уровне значимости, первоначальное предположение подтвердилось, действительно, среднее время решения 3-ей задачи, существенно меньше времени решения 1-ой задачи. В терминах статистических гипотез полученный результат будет звучать так: на5% уровне гипотеза Н0 отклоняется и принимается гипотеза Н1 о различиях.
Критерий Фишера.
Критерий используется для сравнения дисперсий двух выборок с нормальным распределением.
Сравнения дисперсий двух выборок производятся по отношению большей по величине дисперсии(записывается в числителе) к меньшей (записывается в знаменателе). Поэтому значения критерия больше или равно 1,0.
Гипотезы
 : Дисперсия выборке 1 не отличается от дисперсии в выборке 2
: Дисперсия выборке 1 не отличается от дисперсии в выборке 2
 : Дисперсия выборке 1 отличается от дисперсии в выборке 2
: Дисперсия выборке 1 отличается от дисперсии в выборке 2
Ограничения
Данные в выборках должны быть измерены по шкале интервалов или по шкале отношений.
Обе сравниваемые выборки должны иметь нормальный закон распределения.
Алгоритм.
1. Предварительно проверяется нормальность закона распределения по одному из критериев согласия.
2. Рассчитывается средне арифметические значения 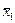 и
и  для каждой выборки по формуле
для каждой выборки по формуле  где
где  – значение i-го результата наблюдения
– значение i-го результата наблюдения
3. Рассчитываются значение  и
и  –дисперсии для каждой выборке по формуле
–дисперсии для каждой выборке по формуле 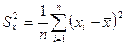
4. Определяется число степеней свободы по выборкам:
 - по первой выборке и
- по первой выборке и  по второй выборке.
по второй выборке.
5. Рассчитывается 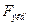 - эмпирическое значение критерия по одной из формул:
- эмпирическое значение критерия по одной из формул:
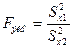 или
или  с учетом того, что дисперсия в числителе должна быть больше дисперсии в знаменателе.
с учетом того, что дисперсия в числителе должна быть больше дисперсии в знаменателе.
6. Найденное эмпирическое значение критерия Фишера 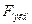 сравнивается критическим значением
сравнивается критическим значением 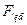 (по таблице 2 приложения) для данного числа степеней свободы
(по таблице 2 приложения) для данного числа степеней свободы  .
.
Если эмпирическое значение 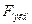 <
< 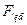 , то нулевая гипотеза
, то нулевая гипотеза  о равенстве дисперсий в выборках при заданном уровне значимости
о равенстве дисперсий в выборках при заданном уровне значимости  принимается.
принимается.
Пример.
В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. Полученные значения величин средних достоверно не различались, однако психолога волнует вопрос – есть ли различия в степени однородности показателей умственного развития между классами.
Решение
Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице
| Номер учащегося | Первый класс | Второй класс |
| Х | Y | |
| Суммы | ||
| Среднее | 60,6 | 63,6 |
Как видно из таблицы, величины средних в обеих группах практически совпадают между собой 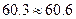 и величина t критерия Стьюдента оказалась равной 0,341 и незначимой.
и величина t критерия Стьюдента оказалась равной 0,341 и незначимой.
Рассчитав дисперсии

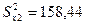
Тогда

По таблице приложения 1 для F критерия при степенях свободы 10-1=9 находим Fкр.

Дата добавления: 2016-04-06; просмотров: 2556;

