Истечение жидкости из малого отверстия в тонкой стенке

Рассмотрим вначале явление истечения капельной жидкости из круглого отверстия диаметром d в вертикальной тонкой стенке сосуда (рисунок11). Давление в сосуде полагаем постоянным (движение установившееся) и равным p₁ Истечение происходит в атмосферу, т.е. наружное давление равно p_ат; площадь отверстия w_o, площадь сечения сосуда w₁. Основные задачи, интересующие инженера, - определение скорости истечения и расхода вытекающей жидкости.

Как показывают опыты, струя жидкости по выходе из отверстия сжимается и на некотором расстоянии от последнего (обычно равным 0,5 диаметра струи) приобретает наименьшую площадь сечения w_c (при диаметре d_c). На рисунке 1 показаны линии токов, сходящиеся к отверстию в тонкой стенке.

a) истечение через малое отверстие в тонкой стенке; b) истечение через насадок. Рисунок 6.1 - Схемысхемы истечения жидкости

Коэффициентом сжатия струи называется отношение площади поперечного сечения струи к площади поперечного сечения отверстия

.

(6.1)

Коэффициентом сжатия струи зависит от отношения площади поперечного сечения отверстия к площади поперечного сечения потока до отверстия

,

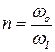(6.2)

которыйКоторый называется степенью сжатия струи n.

Вид функции

.

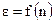(6.3)

определяется формулами, которые были приведены в главе «Местные гидравлические сопротивления».

Если площадь сечения отверстия w_o мала по сравнению с площадью сечения сосуда отверстия (т.е. при n®0, что соответствует случаю так называемого совершенного сжатия), формула Жуковского упрощается к виду

.

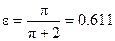(6.4)

Это так называемая формула Кирхгофа.

В обычных условиях при истечении воды из малых отверстий в больших резервуарах опыт дает значения коэффициента сжатия струи, находящегося в пределах

,

(6.5)

т.е. близкие к значению, определяемому формулой (6.5).

Скорость истечения. Для определения скорости истечения напишем уравнение Бернулли для сечений 1-1 и c-c Рисунок 6.2. Плоскость сравнения выберем проходящей через центр тяжести сжатого сечения. Абсолютные давления в сечениях p₁ = p_ат + p_м, p_c = p_ат, значения геодезических отметок z₁ = H, z_c = 0, скорость в первом сечении равна нулю, а во втором сечении равна скорости сжатого сечения v_c. Тогда уравнение Бернулли запишется:

.

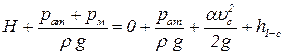(6.6)

Потерями напора между сечениями являются только местное сопротивление на вход в отверстие, которое выражаются через коэффициент z_вхо = 0,06. Поэтому последнее уравнение запишется:

.

(6.7)

Поэтому скорость истечения будет равна

(6.8)

Рисунок 6.2 - Схемы истечения жидкости через отверстие

Введем обозначение

(6.9)

где j - так называемый коэффициент скорости.

В результате формула для скорости истечения принимает вид

(6.10)

При истечении воздуха или воды обычно

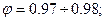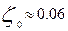
(6.11)

т.е. всего около 2-3% располагаемой разности давлений затрачивается на преодоление сопротивлений.

Расход жидкости, выходящей из отверстия, находим по формуле

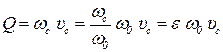
(6.12)

Подставляя вместо значения скорости в сжатом сечении, имеем

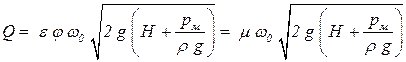
(6.13)

где m = e j - коэффициент расхода отверстия.

В соответствии с формулой (17) коэффициент расхода отверстия 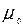представляет собой произведение коэффициента сжатия струи e на коэффициент скорости j.

Значения m для разных n при истечении жидкости с большими числами Рейнольдса приведены в таблице 1.

Таблица 6.1 - -Значение коэффициента расхода отверстия m при различной степени сжатия
n		n
	0,611	0,5	0,678
0,1	0,614	0,6	0,74
0,2	0,622	0,7	0,787
0,3	0,634	0,8	0,888
0,4	0,65	0,9	1,09

При истечении из малых отверстий (n®0) из формулы (17) имеем.