Уравнение простого трубопровода
Рассмотрим вывод уравнения простого трубопровода для схемы короткого трубопровода показанного на рисунке 5.1. Насос из открытого бака перекачивает жидкость в сеть. На входе в насос стоит вакуумметр. Заданы свойства жидкости, материал трубопровода и геометрия трубопровода.
 Рисунок 5.1 - Схема короткого трубопровода
Рисунок 5.1 - Схема короткого трубопровода
|
Для вывода уравнения простого трубопровода в данном случае:
1.5.1.1. Выберем два поперечных сечения там, где известны давления. Нумеруем эти сечения по направлению движения жидкости 1-1 и 2-2. Выбираем плоскость сравнения 0-0 проходящую через центр тяжести нижнего поперечного сечения.
1.5.1.2.Распишем значения z и p в этих поперечных сечениях. Для Рисунок 5.1 z1 = 0, z2 = Hгвв, абсолютное давление в первом сечении равно атмосферному давлению p1 = pат, абсолютное давление во втором сечении равно p2 = pат - pv.
1.5.1.3.Распишем скорости в поперечных сечениях. Площадь первого поперечного сечения гораздо больше площади поперечного сечения трубы, поэтому скорость в первом поперечном сечении гораздо меньше скорости в трубе и примем её равной нулю v1 = 0. Площадь второго поперечного сечения равна площади поперечного сечения трубы, поэтому скорость во втором поперечном сечении равна скорости в трубе v1 = v. Подставим полученные значения в уравнении Бернулли для потока реальной жидкости:
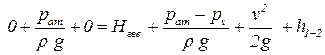 . .
| (5.1) |
Упрощая полученное уравнение, получим
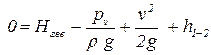 . .
| (5.2) |
1.5.1.4. Находим потери напора в трубопроводе. Потери напора равны сумме потерь напора на местные сопротивления и сумме потерь напора на трение. Местными потерями являются: потери напора на сетке с обратным клапаном, которая ставится на входе в трубу: поворот трубы на 90°; задвижка на трубе. Все эти потери рассчитываются по скорости после местного сопротивления, а это скорость в трубе. По справочникам находим значения коэффициентов этих местных сопротивлений zсетка, zпов, zзад. Потери напора на трение находится по формуле Дарси-Вейсбаха. Тогда потери напора равны
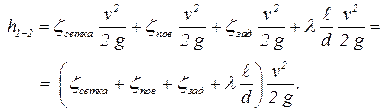
| (5.3) |
1.5.1.4. Подставим потери напора в уравнение Бернулли, получим:
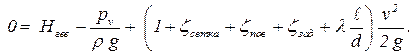
| (5.4) |
Это и есть уравнение простого трубопровода для данного случая. Это уравнение не зависит от типа расчета трубопровода.
Первый тип расчета
Пусть по известным данным необходимо рассчитать давление вакуума pv. В этом случае из уравнения простого трубопровода выразим определяемую величину:
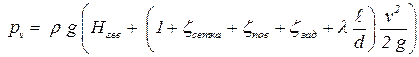
| (5.5) |
Дальнейший порядок расчета следующий:
Рассчитываем объёмный расход Q = V/t;
Рассчитываем скорость в трубе v = Q/w = 4 Q/(p d2);
Рассчитываем число Рейнольдса Re = v d r/m = v d/n и определяем режим движения жидкости в трубопроводе. Если число Рейнольдса меньше критического Reкр = 2000¸2320, то режим движения ламинарный, если больше то турбулентный.
Рассчитываем коэффициент гидравлического сопротивления трения
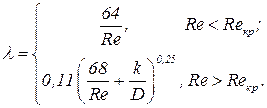
| (5.6) |
Подставляя полученные значения в уравнение (5.5), найдем неизвестную величину.
Второй тип расчета
Пусть по известным данным необходимо рассчитать скорость или расход в трубопроводе. В этом случае уравнения простого трубопровода будет транцентдентным, то есть его нельзя разрешит относительно скорости так, как скорость входит в это уравнение в явном виде, но и в неявном виде при определении коэффициента гидравлического сопротивления трения l. В этом случае возможны два метода расчета: метод подбора и метод итераций.
Метод подбора.
В уравнения простого трубопровода все известные слагаемые перенесём в левую часть, а неизвестные в правую:
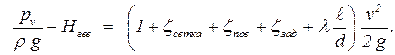
| (5.7) |
Рассчитываем численное значение левой части.
Дальнейший порядок расчета следующий:
Задаемся произвольным значением скорости в трубопроводе v0 (скорость в трубопроводе обычно меньше 5 м/с);
Рассчитываем число Рейнольдса и определяем режим движения жидкости в трубопроводе;
Рассчитываем коэффициент гидравлического сопротивления трения l;
Рассчитываем правую часть уравнения;
Сравниваем рассчитанную правую часть уравнения и левую. Если правая часть уравнения меньше левой Hправ < Hлев то задаёмся большим значением новой скорости v1 > v0, если же правая часть уравнения больше левой Hправ > Hлев то задаёмся меньшим значением новой скорости v1 < v0.
Результаты расчетов удобно поместить в таблицу:
| Скорость, м/с | Re | Режим | l | Hправ |
| V0 | Re0 | l0 | Hправ0 | |
| V1 | Re1 | l1 | Hправ1 | |
| V2 | Re2 | l2 | Hправ2 |
По полученным значениям строим график зависимости правой части уравнения от скорости. Для построения графика необходимо, как минимум три точки. По известной левой части по графику находим необходимую скорость и рассчитываем расход.
Метод итераций
Уравнения простого трубопровода разрешаем относительно скорости:
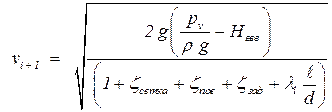
| (5.8) |
Индекс i – номер итерации.
Дальнейший порядок расчета следующий:
Задаемся начальным произвольным значением скорости в трубопроводе v0 с индексом i = 0;
1. Рассчитываем число Рейнольдса и определяем режим движения жидкости в трубопроводе;
2. Рассчитываем коэффициент гидравлического сопротивления трения l0;
3. По уравнению (5.8) рассчитываем новое значение скорости с индексом i = 1.
Далее пункты 1-3 повторяются с новой начальной скоростью. Итерации проводятся до тех пор, пока первые три значащие цифры скорости не совпадут. Для турбулентного режима движения обычно необходимо провести две - три итерации, для ламинарного режима движения итераций необходимо больше.
Третий тип расчета
Пусть по известным данным необходимо рассчитать диаметр трубопровода. В этом случае уравнения простого трубопровода будет транцентдентным, то есть его нельзя разрешит относительно диаметра так, как диаметр входит в это уравнение в явном виде, но и в неявном виде при определении коэффициента гидравлического сопротивления трения l. В этом случае возможны два метода расчета: метод подбора и метод итераций.
Метод подбора.
В уравнения простого трубопровода все известные слагаемые перенесём в левую часть, а неизвестные в правую:
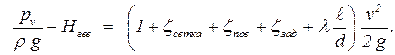
| (5.9) |
Рассчитываем численное значение левой части.
Дальнейший порядок расчета следующий:
Задаемся начальным произвольным значением диаметра трубопровода d0. Начальное значение диаметра очень трудно угадать. Поэтому в первом приближении можно считать, что максимальная скорость в трубопроводе равна vмах = 5 м/с, тогда по известному расходу можно найти начальную площадь поперечного сечения и диаметр трубопровода:
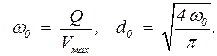
| (5.10) |
Рассчитываем число Рейнольдса и определяем режим движения жидкости в трубопроводе;
Рассчитываем коэффициент гидравлического сопротивления трения l;
Рассчитываем правую часть уравнения;
Сравниваем рассчитанную правую часть уравнения и левую. Если правая часть уравнения меньше левой Hправ < Hлев то задаёмся меньшим значением нового диаметра d1 < d0, если же правая часть уравнения больше левой Hправ > Hлев то задаёмся большим значением новой скорости нового диаметра d1 > d0.
Результаты расчетов удобно поместить в таблицу:
| Диаметр, м/с | Re | Режим | l | Hправ |
| d0 | Re0 | l0 | Hправ0 | |
| d1 | Re1 | l1 | Hправ1 | |
| d2 | Re2 | l2 | Hправ2 |
По полученным значениям строим график зависимости правой части уравнения от диаметра. Для построения графика необходимо, как минимум три точки. По известной левой части по графику находим необходимый диаметр.
Метод итераций
В уравнения простого трубопровода выразим скорость через расход:
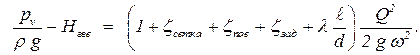
| (5.11) |
Найдем из этого уравнения площадь поперечного сечения w. В уравнения простого трубопровода разрешаем относительно диаметра:
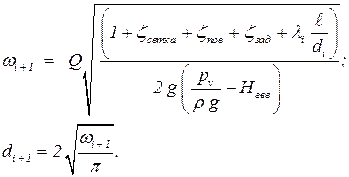
| (5.12) |
Индекс i – номер итерации.
Дальнейший порядок расчета следующий:
Задаемся начальным произвольным значением диаметра трубопровода d0 с индексом i = 0;
1. Рассчитываем площадь поперечного сечения wi = p di2/4.
2. Рассчитываем среднюю скорость в поперечном сечении vi = Q/wi.
3. Рассчитываем число Рейнольдса и определяем режим движения жидкости в трубопроводе;
4. Рассчитываем коэффициент гидравлического сопротивления трения li;
5. По уравнению (5.12) рассчитываем новое значение диаметра с индексом i = 1.
Далее пункты 1-5 повторяются с новым начальным диаметром. Итерации проводятся до тех пор, пока первые три значащие цифры диаметра не совпадут. Для турбулентного режима движения обычно необходимо провести две - три итерации, для ламинарного режима движения итераций необходимо больше.
Формула для обоснования ориентировочного значения внутреннего диаметра нефтепровода D0 [2]:
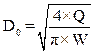 , (5.13)
, (5.13)
где: Q – секундная подача, м3/с;
W – скорость перекачки, м/с.
По ориентировочному значению D принято ближайший стандартный Dн наружный диаметр.
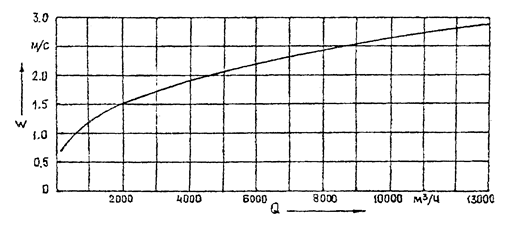
Рисунок 5.1 - Зависимость рекомендуемой скорости перекачки от плановой пропускной способности нефтепровода
Формула Лейбензона. Для точных расчетов лупингов (вставок) используется метод последовательных приближений, изложенный в 5.4.9. Для приближенных расчетов по формулам (5.26)-(5.31) в качестве исходной применяется обобщенная формула Лейбензона [2], которая связывает гидравлический уклон i на участке трубопровода диаметром d с производительностью перекачки Q при заданной вязкости жидкостиn :
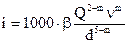 , (5.25)
, (5.25)
где: b, m – коэффициенты, определяющие характер течения в трубопроводе. Зависят от числа Рейнольдса в трубопроводе и граничного числа Рейнольдса Re1. На практике при реальных режимах перекачки по стальным трубам для граничного числа Рейнольдса может быть принята приближенная оценка: 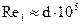 ; b, m - определяются согласно таблице 5.14.
; b, m - определяются согласно таблице 5.14.
n – кинематическая вязкость жидкости, м2/с;
Q – производительность перекачки, м3/с;
d – диаметр трубопровода, м.
Таблица 5.14 – Значение коэффициентов b, m формулы Лейбензона
| Условия для числа Рейнольдса | Характер течения в трубопроводе | Значение m | Значение b, с2/м |
| Re < 2300 | Ламинарный режим | 4,15 | |
| 2300 < Re < Re1 | Турбулентный режим в зоне Блазиуса | 0,25 | 0,0246 |
| Re > Re1 | Турбулентный режим в зоне смешанного трения | 0,123 | 0,00585 |
Дата добавления: 2016-04-06; просмотров: 1537;
