Экспериментальные исследования коэффициента гидравлического сопротивления

Экспериментальным определением зависимости падения давления от расхода жидкости в трубах и каналах начали заниматься более 200 лет тому назад. Почти каждый исследователь получал свой, отличный от других, закон сопротивления. Это было связано с тем, что в опытах различных авторов не соблюдался закон подобия, установленный О. Рейнольдсом в конце XIX века. Кроме того, не учитывалось, что в разных опытах стенки имели различную шероховатость.

Первые систематические опыты для выяснения зависимости коэффициента гидравлического сопротивления λ от Re и шероховатости стенок труб были проделаны Никурадзе в конце 20-х - начале 30-х годов XX века в Геттингенском университете. Опыты производились на гладких латунных трубах и трубах с искусственной равномерной шероховатостью. Такая шероховатость получалась путем наклейки на стенки трубы песчинок определенного размера, для чего песок предварительно просеивался через специальные сита. Размер зерен песка принимался за размер зерен шероховатости ∆.

Результаты опытов Никурадзе в координатах lg(l) – lg(100 Re)представлены на рисунке 4.95, где е = k/D. Из этих опытов, проведенных в широком диапазоне значений числа Рейнольдса, следует, что существует 5 областей для коэффициента гидравлического сопротивления.

Рисунок 4.7 - Обработка– обработка опытов Никурадзе.

В первой области (прямая I) при Re < 2300 режим течения ламинарный и λ зависит от Re, но не зависит от k/D. Для этой области справедлива формула:

.

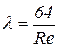(4.25)

Во второй области имеет место переходный область от ламинарного режима движения к турбулентному режиму. Коэффициент λ возрастает и зависит только от Re.

Третья область (прямая II) - так называемая область гидравлически гладких труб. Трубы с различной шероховатостью ведут себя как гладкие, то есть λ зависит только от Re. При этом границы области зависят от k/D. Чем больше k/D, тем уже эта область. При достаточно больших k/Dтретья область исчезает. Для этой области справедлива формула Блазиуса:

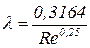
(4.26)

Четвертая область - область смешанного трения или область доквадратичного сопротивления. Коэффициент λ зависит как от Re, так и от k/D. В этой области существует достаточно много формул, но удобно пользоваться формулой Альтшуля:

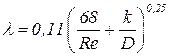
(4.27)

Пятая область - область квадратичного трения. Коэффициент λ зависит только от k/D.

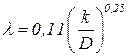
(4.28)

При выполнении вычислений на ЭВМ удобно использовать формулу Черчилля, справедливую во всем диапазоне чисел Рейнольдса, включая ламинарный режим течения:

(4.29)

Примеры и задачи

Пример 4.1.

Дано:

Определить пределы изменения гидравлического радиуса К для канализационных самотечных трубопроводов, если диаметр их <1 изменяется от 150 до 3500 мм. Расчетное (наибольшее) наполнение: а=п/с1=0.6 для труб (1=150 мм; а=Ь/ё=0.8 для труб (1=3500 мм.

Решение:

Гидравлический радиус определяем по формуле:

к = -X

где

Угол находимйиаходим из соотношения:

Пример 4.2.

81п а=0.6-0.5-1=0.2; а=0.2 рад; ф=3. 14+2*0.2=3.54 рад;

4 6,2о

5С=3. 14*0. 15*3.54/6.28=0.266 м;

К=0.011 1/0.266=0.0417 м. Для трубы (1=3500 мм:

81п а=0.8/0.5-1=0.6; а=0.63 рад; ф=3. 14+2*0.63=4.4 рад;

+ 3,5² (0,8 - 0,5)ДЩГ^] = 8Д2М²

Х=3. 14*3.5*4.4/6.28=7.7 м;

К=8.22/7.7=1.07м. Таким образом, гидравлический радиус изменяется от 0,04 до 1,07 м.

Пример 4.3.

Определить напор, необходимый для пропуска расхода воды Q=0,=0.01 м3/с через трубопровод диаметром (1=0,3 м и длиной 1=1200 м. Трубы стальные новые. Температура 20 градусов С.

Решение:

По таблице находим эквивалентную шероховатость новых стальных труб 1сэ=ОЛмм. Для найденной шероховатости и заданного диаметра определяем значение удельного сопротивления трубопровода при работе его в квадратичной области: Акв=0,504 с²/м⁶

Требуемый напор (в первом приближении) при условии работы трубопровода в квадратичной области

п_кв=А_кв!д²=0.5*1200*0.07²=Зм.

Скорость движения воды в трубе

^ 40 4*0.07 v = ^ =

со ж/² 3.14*0.3²

Определяем по таблице поправку на неквадратность: х|/=1,1 и получаем необходимый напор:

Задача 4.1

Определить расход воды р в трубе диаметром д1=250мм, имеющей плавное сужение до диаметра &2~ 125мм, если показания пьезометров: до сужения: П1=50см; в сужении П2=30см. Температура воды 20 градусов С.

Задача 4.2

Определить, на какую высоту поднимается вода в трубке, один конец которой присоединен к суженному сечению трубопровода, а другой конец опущен в воду. Расход воды в трубе р=0,025 м3/с, избыточное давление р!=49*10³ Па, диаметры д1=100мм и д2=50мм.

Задача 4.3

Выход воды из горизонтальной песколовки выполнен в виде сужения с плавно закругленными стенками. Ширина песколовки В=3м. Расход сточной воды <3=0,9 м3/с при скорости движения воды У1=0,3 м/с. Определить глубину воды в отводящем канале П2, если ширина его Ъ=0,8м.

Задача 4.4

Стальной новый водовод диаметром ё=0,25м, с абсолютной эквивалентной шероховатостью 1со=0,0001м имеет пропускную способность (Зо⁼⁼0,052м³/с. Вода в источнике слабоминерализованная, некорозионная. Исследования, проведенные через два года после начала эксплуатации, показали, что абсолютная шероховатость трубопровода возросла до К2⁼0,2мм. Требуется определить, какая будет пропускная способность водовода СЬз через 15 лет эксплуатации.

Задача 4.5

Потеря давления в стальной водопроводной трубе диаметром с1=0,45м и длиной 1=3 000м, бывшей в эксплуатации в течение 12 лет, составляет р12=10⁵Па при расходе воды СЬ2=0,2м³/с. Температура воды 20 градусов С. Требуется определить потери давления р2о в этой же трубе через 20 лет эксплуатации при расходе воды 02о⁼0,3 м /с.

Задача 4.6

Определить величину повышения давления в стальной водопроводной трубе, если скорость воды в трубе до удара была у=1м/с, диаметр трубы ё=0,5м, и толщина стенок 8=0.0005.