ЛаминарныйЛаминарный режим движения
Ламинарный режим движения существует в трубах, если число Рейнольдса меньше критического числа Рейнольдса Re < Reкр = 2000¸2320. Закон Ньютона внутреннего трения для круглой трубы запишется
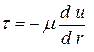 . .
| (4.13) |
Подставляя касательные напряжения в уравнение равномерного движения, получим:
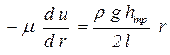 . .
| (4.14) |
Разделим переменные, для этого дифференциал скорости перенесём в левую часть уравнения, а всё остальное в правую
 . .
| (4.15) |
Интегрируем это уравнение в пределах от радиуса r, где местная скорость равна u, до радиуса трубы r0. где скорость равна нулю:
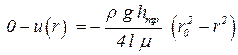 , ,
| (4.16) |
Тогда распределение скорости в поперечном сечении трубы при ламинарном режиме движение происходит по параболическому закину
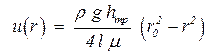 , ,
| (4.17) |
Расход жидкости равен сумме расходов по элементарным струйкам, имеющим площадь кольца dw = 2 p r d r
 . .
| (4.18) |
Средняя скорость в трубе равна
 . .
| (4.19) |
Из последней формулы следует, что средняя скорость в трубе при ламинарном режиме движения равна половине максимальной скорости. Из последней формулы найдем потери напора на трение
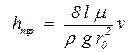 . .
| (4.20) |
Эта формула носит название формулы Пуазейля. Из неё следует, что потери напора на трение пропорциональны средней скорости в трубе и обратно пропорциональны квадрату радиуса трубы. Но в общем случае потери напора на трение рассчитываются по формуле Дарси-Вейсбаха, поэтому сравнивая формулы (4.19) и (4.3)
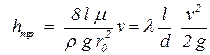
| (4.21) |
получим значение для коэффициента гидравлического трения
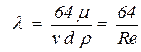
| (4.22) |
Дата добавления: 2016-04-06; просмотров: 676;
