Ламинарное и турбулентное движение жидкости

Наблюдения показывают, что в природе существуют два различных вида движения жидкости: во-первых, слоистое упорядоченное, или ламинарное, движение, при котором отдельные слои жидкости скользят относительно друг друга, не смешиваясь между собой, и, во-вторых, неупорядоченное, или турбулентное, движение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание. Уже давно известно, что вязкие жидкости (масла) движутся большей частью упорядочение, а маловязкие жидкости (вода, воздух) - почти всегда неупорядоченно. Ясность в вопросе о том, как именно будет происходить движение жидкости в тех или иных условиях, была внесена в 1883 году в результате опытов английского физика Рейнольдса.

Рисунок 4.1 - Опыты Рейнольдса.

В опытной установке Рейнольдса (рисунок 4.2) к баку с водой 2 присоединена стеклянная труба 4. Открывая частично вентиль 5, можно заставить течь воду по трубе с различными скоростями. Из сосуда по трубке в устье трубы поступает краска из бачка 1 по трубке 3. При малых скоростях движения воды в трубе окрашенная струйка не размывается окружающей ее водой и имеет вид натянутой нити (рисунок 4.2, а) - поток в этом случае называют ламинарным. При увеличении скорости движения воды, окрашенные струйки получают вначале волнистое очертание и при этом изменяются с течением времени (рисунок 4.2, б)) - поток в этом случае называют переходной областью. При дальнейшем увеличении степени открытия крана, увеличивается скорость движения жидкости, и окрашенные частицы размываются по всему сечению трубы и окрашивая всю жидкость. Движение жидкости становится неупорядоченным, отдельные частицы окрашенной жидкости разлетаются в разные стороны, сталкиваются друг с другом, ударяются о стенки и т. д. (рисунок 4.4, с). Такое движение жидкости называют турбулентным. Основная особенность турбулентного движения заключается в наличии поперечных к направлению движения составляющих скорости, накладывающихся на основную скорость в продольном направлении. Из опытов Рейнольдса следует, что существует только два режима движения жидкости ламинарный и турбулентный и переходная область между ними. Опыты Рейнольдса показали, что переход от ламинарного течения к турбулентному происходит при определенной скорости (так называемая критическая скорость), которая, однако, для труб разных диаметров оказывается различной, возрастающей с увеличением вязкости и снижающейся с уменьшением диаметра трубы. Наличие режимов движения отражается на потерях напора на трение. При ламинарном режиме движения потери напора пропорциональны скорости, а при турбулентном режиме потери напора пропорциональны скорости в степени 1,75 – 2, что показано на рисунке

Рисунок 4.2 -– зависимость потерь напора на трение от скорости

Основываясь на некоторых теоретических соображениях, а также на результатах опытов, Рейнольдс установил общие условия, при которых возможны существование ламинарного и турбулентного режимов движения жидкости и переход от одного режима к другому. Оказалось, что состояние (режим) потока жидкости в трубе зависит от безразмерного числа, которое учитывает основные факторы, определяющие это движение: среднюю скорость v, диаметр трубы d, плотность жидкости r и ее абсолютную вязкость m.. Это число (позже оно стало называться числом Рейнольдса) имеет вид:

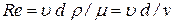
(4.5)

Диаметр d в числе Рейнольдса может быть заменен любым линейным диаметром, связанным с условиями течения или обтекания (диаметр трубы, диаметр падающего в жидкости шара, длина обтекаемой жидкостью пластинки и др.).

Число Рейнольдса, при котором происходит переход от ламинарного движения к турбулентному, называют критическим и обозначают Re_кр. При Re > Re_кр - режим движения является турбулентным, при Re < Re_кр - ламинарным. Критическое число Рейнольдса зависит от условий входа в трубу, шероховатости ее стенок, отсутствия или наличия первоначальных возмущений в жидкости, конвективных токов и др.

Вопрос о неустойчивости ламинарного движения и о его переходе в турбулентное, а также о величине критического числа Рейнольдса подвергался тщательному теоретическому и экспериментальному изучению, но до сих пор не получил еще достаточно полного решения. Наиболее часто в расчетах принимают для критического числа Рейнольдса при движении жидкости в трубах значение

,

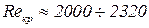(4.6)

отвечающее переходу движения жидкости из турбулентного в ламинарное: при переходе движения из ламинарного в турбулентное критическое число Рейнольдса имеет большую величину (для хорошо закругленного плавного входа оно может быть доведено до 20000).

Проведенные исследования показывают также, что критическое число Рейнольдса увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах усиливается.

По критическому числу Рейнольдса легко можно найти также критическую скорость, т. е. скорость, ниже которой всегда будет происходить ламинарное движение жидкости:

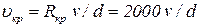
(4.7)

Предположив, что режим движения зависит только от четырех величин: v, d, r и m которые имеют размерность:

Так, как режим движения не имеет размерности, то в правой части должна быть безразмерная величина. Из оставшихся величин, последовательно, исключая размерности массы, времени и расстояния можно получить безразмерный параметр, который и будет числом Рейнольдса.