Векторная концепция электрокардиографии
Представление о том, что электрическое поле сердца на поверхности тела можно характеризовать не только величиной потенциалов, но и определенным направлением распространения процесса, возникло почти с первых шагов развития электрокардиографии как метода клинической диагностики. Однако судить об ориентации процесса только на основании величины потенциала лишь одного какого-либо отведения не представляется возможным. W. Einthoven (1908 -1913) доказал, что для оценки направления требуется сопоставление показателей ЭКГ нескольких отведений (минимум двух), располагающих определенными свойствами. Комплекс из таких отведений составляет так называемые системы отведений. Свойствами отведений являются равноудаленность от сердца расположения электродов, малая чувствительность отведений к небольшим смещениям электродов, равенство осей отведений между собой и преобладание их длины над размерами сердца.
В клинической электрокардиографии классической геометрической схемой отведений считается разработанная Эйнтховеном для фронтальной плоскости «схема равностороннего треугольника». Эйнтховен, выбравший для формирования трех отведений положение электродов на двух руках и левой ноге и объединив попарно эти позиции, предложил рассматривать данные отведения как стороны равностороннего треугольника, в центре которого расположено сердце. При этом предусматривалось такое соединение электродов с полюсами гальванометра (так называемая полярность отведений), при котором в каждом из трех отведений основные элементы нормальной ЭКГ (зубцы P,R и T) регистрируются вверх от изоэлектрической линии, когда значение основания сердца или правой руки отрицательно по отношению к верхушке сердца или левой руке, а зоны положительного потенциала поверхности тела соединены с положительным полюсом гальванометра.
На рис. 15, а показаны взаиморасположение и полярность трех (I,II,III) отведений системы Эйнтховена. Относительное значение полюсов каждого из отведений показывает, что движение тока от положительного полюса отведения к отрицательному (в направлении падения потенциала) происходит в I и III отведениях в одном направлении (против часовой стрелки), а воII отведении в прямо противоположном направлении (по часовой стрелке). Поэтому и физические характеристики (напряжение e, сила тока i) второго отведения рассматриваются в обратной (отрицательной) полярности (-e2, -i2), а само отведение - как -II по сравнению с отведениями +I и +III.

Рис. 15. Три классических отведения Эйнтховена (I, II, III):а - положение электродов на теле (R - правая рука; L - левая рука, F- левая нога), полярность отведений и отношение между регистрирующимися потенциалами по отведениям (e1, e2, e3)и сердечным вектором; e1 - e2 + e3 = 0; e1 + e3 = e2; I + III = II; б- равносторонний треугольникЭйнтховена, манифестирующий вектор pq и его проекции на стороны треугольника (p1q1, p2q2, p3q3); H- центр треугольника
Кроме условия, относящегося к полярности отведений, для воспроизведения системы треугольника Эйнтховена были приняты еще три необходимых допущения:
· сердце расположено в центре гомогенной среды тела;
· сердце значительно отдалено и равноотстоит от трех точек, формирующих отведения, и рассматривается по отношению к ним как материальная точка;
· сопротивления на пути от сердца к каждой точке отведения равновелики.
Сформулированные Эйнтховеном условия и допущения позволяют рассматривать созданную им систему с геометрической точки зрения (свойства равностороннего треугольника) и с точки зрения законов постоянного тока (замкнутый трехфазный контур) в качестве системы отведений, равноотстоящих от сердца как центрально расположенного точечного источника тока.
Это позволяет все множество разностей потенциалов, существующих в данный момент по разным направлениям объема мышечной массы сердца, представить в виде единой результирующей величины разности потенциалов, ориентирующейся в определенном пространственном направлении относительно своей исходной точки соответственно любому моменту возбуждения. Или результирующая разность потенциалов каждого данного момента является также и средней геометрической из множества разнонаправленных путей, по которым воспроизводятся разности потенциалов. Впоследствии эта пространственная результирующая получила название среднего моментного вектора сердца.
Отражение на фронтальной плоскости тела через «систему треугольника» пространственной результирующей рассматривается как её фронтальная проекция, которая применительно к основному моменту разности потенциалов была названа Эйнтховеном манифестирующей величиной разности потенциалов. Связь между ней и величиной отклонений каждого из трех отведений вытекает из отношения направления манифестирующей величины к направлению осей отведений и демонстрируется схемой эйнтховенского треугольника отведений.
На рис. 15, б стрелкой показано направление манифестирующей величины в момент максимального значения разности потенциалов. Если манифестирующий вектор Е имеет в данный момент абсолютное значение pq, то разности потенциалов в каждом из трех отведений (e1, e2, e3) окажутсянеодинаковыми по абсолютному значению (p1,q1,p2, q2,p3, q3), отражающему проекцию под разными углами одной и той же величины (манифестирующей) на оси отведений. Если известно, в каком направлении фронтальной плоскости регистрируется манифестирующая величина, т. е. угол между ней и, например, осью Iотведения (уголa), то можно не только изобразить графически величины разности потенциалов в трех отведениях, но и определить их численное значение.
Последнее вытекает из свойств геометрических фигур, образующихся при данном построении:
· Каждый угол равностороннего треугольника RLF, сформированного из трех отведений, равен 600.
· Манифестирующая образует со своими тремя проекциями на стороны равностороннего треугольника RLF три прямоугольных треугольника, в которых она является гипотенузой (специальные построения, не приводимые на рис.15, б). Используя тригонометрические функции (значение сosa), по известному углу a и гипотенузеE выводят значение разности потенциалов в каждом из трех отведений.
Для определения неизвестного угла a (или направления манифестирующей), когда известна разность потенциалов отдельных отведений (минимум двух), используют тангенциальные тригонометрические функции. Угол a рассматривается Эйнтховеном как положительный, если манифестирующая отклоняется отI отведения по часовой стрелке (вниз от I отведения), и как отрицательный при её перемещении против часовой стрелки (вверх отI отведения).
Показанная Эйнтховеном закономерность, согласно которой величина отклонений ЭКГот изоэлектрической линии воII отведении равняется сумме одномоментных величин ЭКГ в I и III отведениях, вытекает из основных геометрических и физических свойств системы с учетом обратной полярности II отведения:
1) проекция вектора на одну из сторон равностороннего треугольника равняется сумме его проекций на две другие стороны или I и III отведения равняются II(I + III - II = 0);
2) согласно второму закону Кирхгофа в замкнутом контуре сумма напряжений его отдельных ветвей равнанулю, или применительно к трехфазному контуру Эйнтховена e1 + e3 - e2 = 0(e1 + e3 = e2).
Учитывая эти свойства системы (e1 + e3 = e2), H. Mann в 1920 г. с помощью геометрических построений показал соотношение между полярной системой Эйнтховена и прямоугольной системой координат, на основании которой возможно более простое построение манифестирующей с отведений Эйнтховена, так как ось x (горизонталь, абсцисса прямоугольных координат) соответствует значению I отведения e1, а ось y (вертикаль, ордината) выводится из значений II и III отведений и соответствует значению (e2 + e3 ) / Ö 3 .
Чтобы составить представление о манифестирующей разности потенциалов сердца по электрокардиографическим кривым, зарегистрированным в трех стандартных отведениях Эйнтховена, можно использовать два приема:
· манифестирующую величину выводят из значения минимум двух отведений, отнесенных к полярной системе координат Эйнтховена;
· манифестирующую величину выводят из значения трех стандартных отведений, отнесенных к прямоугольной системе координат.
Таким образом, концепция Эйнтховена о векторных свойствах электрического поля на поверхности тела есть основополагающий принцип для дальнейшей разработки теории электрического поля сердца с позиций представлений о едином сердечном диполе и обоснований принципов современной векторной электрокардиографии.
Векторная концепция электрокардиографии нашла свое дальнейшее развитие в исследованиях Burger A. и Van Milaan J. (1947 - 1948). Согласно их представлениям общий электрический эффект, возникающий при возбуждении сердца, является результатом электрической активности всех его мельчайших отделов. Степень участия этих отделов в формировании электрического поля сердца пропорциональна объему каждого из них и напряженности создающихся ими элементарных электрических полей. Поскольку каждое из множества элементарных полей занимает некоторый объем в данной среде, их суммарное поле тока также распространяется по всем направлениям проводящей среды и может рассматриваться в качестве векторной суммы сил всех элементарных электрических полей сердца. Такая векторная сумма может быть представлена в виде одной результирующей, имеющей значение единого сердечного вектора, который своей величиной и пространственной ориентацией отражает в каждый данный момент сердечного цикла комбинированный эффект множества электрических полей и определяет характер электрического поля на поверхности тела.
Как любая величина, характеризующаяся каким-либо направлением в пространстве, результирующий сердечный вектор H находится тремя взаимно перпендикулярными пространственными компонентами, исходящими из его начальной точки (рис. 16). Применительно к оценке сердечного вектора в расчет принимаются три его компонента, направление которых соответствует декартовой системе координат, поскольку с ней согласуются горизонтальная (х), вертикальная (у) и сагиттальная (z) условные оси тела. На рис. 16 показано соотношение сердечного вектора H(х,у,z) и его трех взаимно перпендикулярных компонент, обозначаемых как компонентых, у, z.
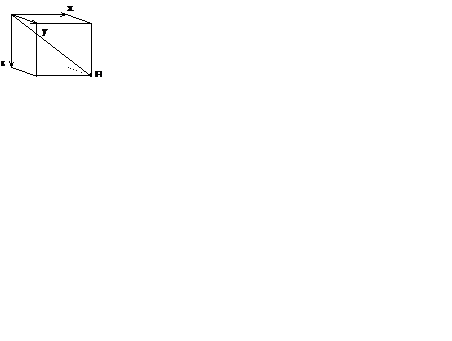
Рис. 16. Сердечный вектор H и три его пространственных компонента
Оси любого электрокардиографического отведения также имеют определенное отношение как к направлению пространственных координат, так и к направлению сердечного вектора и трех его компонент. При этом на разность потенциалов, фиксирующихся в каждом отведении, будут влиять величина и пространственная ориентация сердечного вектора H(х,у,z) и, следовательно, трех его компонентов х, у, z , а также физические свойства тела, существующие в направлении трех компонентов сердечного вектора, - показателей a, b, c (рис. 17).

Рис. 17. Отношение между сердечным вектором H и вектором отведения (a, b, c)
Показатели a, b, c зависят, с одной стороны, от формы, размеров, электропроводности и некоторых других физических свойств тела, т.е. отражают скалярные характеристики среды, а с другой - от выбранных осей отведений, в направлении которых проявляется то или иное количественное значение этих физических свойств. Иначе говоря, значение каждого из показателей a, b, c, будучи постоянным для одного и того же отведения, изменяется в достаточно широких пределах в зависимости от направления отведений, т.е. оно может рассматриваться как векторная функция отведения.
Результат взаимодействия показателей a, b, c относительно оси каждого данного отведения получил название вектора отведения (a, b, c).Отношение между вектором отведения и сердечным вектором вытекает из геометрических построений (см. рис. 17) и определяется формулой, по которой разность потенциалов отведения равна произведению результирующего вектора на вектор отведения и косинус угла между ними: отведение = (x, y, z) · (a, b, c) · cos j(формула Бургера). Согласно дипольной концепции формулу отведения Бургера рассматривают как произведение проекции сердечного диполя (=x, e, z, cos a)на длину вектора отведения (Frank E., 1956).
Представление о результирующем векторе как отражении моментного суммарного эффекта электрической деятельности сердца, вытекающее из концепции Бургера, и понятие о «векторе отведения» играют большую роль в обосновании векторных принципов анализа в современной электрокардиографии. Результирующий вектор лежит в основе воспроизведения разности потенциалов на поверхность тела, вектор отведения модифицирует её в зависимости от положения электродов на теле, формула отведения показывает зависимость зарегистрированной величины разности потенциалов от этих двух факторов.
Подобно результирующему вектору три составляющих его компонента x, y, z также находятся в определенном отношении к вектору отведения. Каждое из отведений отражает одну из составляющих сердечного вектора тем полнее, чем меньше угол между данным компонентом и осью отведения. В случае, если один из компонентов параллелен оси отведения и, следовательно, два других перпендикулярны ей, то значение разности потенциалов этого отведения будет отражать величину параллельного ему компонента, значение же двух других для этого отведения будет сводиться к нулю.
При условии физической однородности среды, находящейся между осью отведения и сердечным вектором, отведение отражает результирующий вектор или его компоненты достаточно адекватно в случае, если позиции двух электродов, формирующих ось отведения, находятся на равном расстоянии от сердца (от его «нулевого» или «электрического» центра) или, тогда, когда значение потенциала под одним из регистрирующих электродов приближается к нулю (скорее к величине, которой можно пренебречь). Поэтому позиция такого электрода может быть соотнесена с положением исходной нулевой точки сердечного вектора (специальные, так называемые «однополюсные» отведения). Так как тело человека имеет сложную конфигурацию (сердце в нем расположено эксцентрично, а окружающая сердце среда неоднородна), то физически обоснованный выбор позиции пары электродов для регистрации с поверхности тела ЭКГ, которая не искажала бы истинных характеристик результирующего вектора (и его составляющих), остается до последнего времени достаточно сложной проблемой векторной электрокардиографии.
Векторкардиография
Векторкардиография представляет собой метод пространствен-ного динамического исследования электрического поля сердца в процессе кардиоцикла. В основе метода лежит принцип получения пространственной фигуры, являющейся графическим изображением изменений величины и направления электродвижущей силы в течение всего сердечного цикла. Известно, что при возбуждении мышцы сердца во все моменты сердечного цикла образуется значительное количество разнонаправленных моментных векторов, оценка каждого из которых невозможна. Это дало основание интегрировать их и при анализе оперировать понятием результирующего вектора сердца, являющегося суммой элементарных векторов каждого момента электрической активности миокарда. В процессе периодов возбуждения и восстановления сердечного цикла измеряют величину и направление результирующего вектора сердца, описывающего в пространстве из предполагаемого центра сердца кривую, названную векторкардиограммой (ВКГ). В векторкардиографии принята своя система координат, для перехода к которой от обычной Декартовой системы координат следует учитывать, что Х = -х, Y = -z, Z = -y (рис. 18)
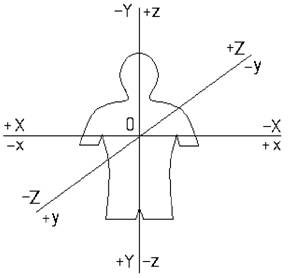
Рис. 18. Декартова система координат xyz и XYZ, используемая в векторном и топографическом анализе ВКГ. Три плоскости XZ, XY, и YZ, образованные этими осями координат, представляются как горизонтальная, фронтальная и сагиттальная плоскости соответственно. Существует два способа представления векторкардиограммы: скалярное и векторное.
Скалярное представление векторкардиограммы:Скалярное представление ВКГ вполне соответствует общепринятому представлению стандартной электрокардиограммы (ЭКГ) в двенадцати отведениях – измеренные сигналы изображаются в виде кривых изменения потенциала во времени для каждого отведения. Основные элементы каждой кривой ВКГ также аналогичны элементам стандартной ЭКГ. На рисунке 19 представлено упрощенное изображение скалярной ВКГ в одном отведении, содержащее все типичные элементы.
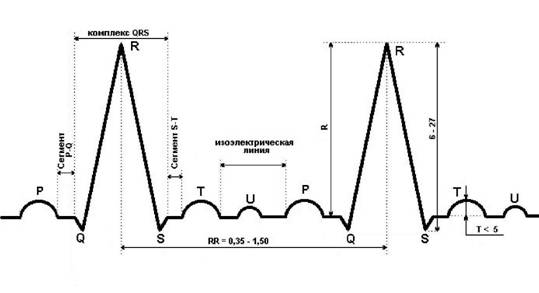
Рис. 19. Типичный кардиоцикл скалярной ортогональной электрокардиограммы в отведении Х
Наибольшее по амплитуде, относительно быстрое отклонение, отражающее процесс деполяризации желудочков сердца называют комплексом QRS. Комплекс QRS, или желудочковый комплекс, отра-жает деполяризацию желудочков. Продолжительность его от начала зубца Q до начала зубца S не превышает 0,1 сек., и чаще всего он равен 0,06 или 0,08 сек. Измерение его производится в том отведении, где ширина его наибольшая. За комплексом QRS следует пологий или почти горизонтальный участок - сегмент S-T, соответствующий началу реполяризации желудочков, который переходит в отклонение, соот-ветствующее конечной, быстрой реполяризации желудочков – зубец Т. После зубца Т в некоторых случаях удается зарегистрировать зубец U. Происхождение его до сих пор не совсем выяснено. Есть основание считать, что он связан с реполяризацией волокон проводящей систе-мы. Он возникает через 0,04 сек после зубца Т. Перед комплексом QRS обычно имеется отклонение, которое имеет ровную округлую форму, характеризующее процесс деполяризации предсердий и называемое зубцом Р. Горизонтальный участок кардиограммы между зубцом Т (или U) одного из кардиоциклов и зубцом Р последующего кардиоцикла обычно используется в качестве истинной изолинии, относительно которой можно измерять значения всех представляющих интерес отклонений. Основные измеряемые параметры скалярной ВКГ - это амплитуда и длительность каждого зубца, а также длительность некоторых характерных комплексов и участков, которые могут включать несколько зубцов и промежутков между ними. Интервал PQ отражает время, необходимое для деполяризации предсердий и проведения импульса по атриовентрикулярному (АВ) соединению, его называют предсердно-желудочковый интервал. Его измеряют от начала зубца Р до начала желудочкового комплекса – зубца Q или зубца R при его отсутствии. В норме продолжительность интервала Р-Q колеблется от 0,12 до 0,20 сек и зависит от частоты сердечных сокращений, пола и возраста исследуемого. Увеличение интервала P-Q характеризуется как нарушение AВ- проводимости.
Векторное представление векторкардиограммы:Векторкардиограмма, как в норме, так и при патологии состоит из следующих элементов (рис. 20):
1. Изоэлектрическая (нулевая) точка.
2. Петля Р, являющаяся отражением процессов возбуждения мио-карда предсердий, на скалярной ЭКГ ей соответствует зубец Р.
3. Петля QRS, являющаяся отражением возбуждения миокарда же-лудочков, на скалярной ЭКГ ей соответствует комплекс QRS:
· Начальное отклонение, соответствующее по времени появлению зубца Q на скалярной ЭКГ.
· Тело петли, в котором принято различать нисходящую (центро-бежную) и восходящую (центростремительную) части.
· Конечное отклонение, соответствующее по времени появлению зубца S на скалярной ЭКГ. Петля Т, являющаяся отражением про-цесса восстановления (реполяризации) миокарда желудочков. На ЭКГ ей соответствует зубец Т.
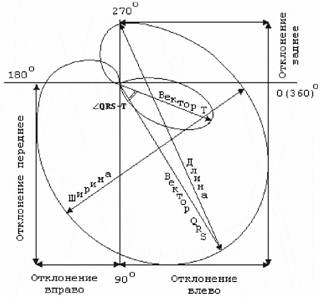
Рис. 20. Векторная петля на плоскости и ее основные параметры.
Интервалы Р-Q, S-Т, Т-Р на ВКГ не видны, так как в моменты, соответствующие отсутствию разности потенциалов, конец вектора сердца возвращается в нулевую точку. При анализе ВКГ определяют плоскостные и пространственные показатели динамики электрического поля сердца человека. При анализе плоскостных показателей векторной петли рассматривают проекции петель на координатные плоскости. При анализе векторной петли в каждой плоскости определяют:
1. длину и ширину петли QRS и их соотношение;
2. отклонение вперед, назад, влево и вправо и их отношения в вертикальной, горизонтальной и сагиттальной плоскостях;
3. величину и направление максимального вектора петель QRS и T;
4. величину и направление моментных векторов (обычно моментные векторы определяются через каждые 0,01 с);
5. угол расхождения между направлением максимальных векторов QRS и T (ےQRS-T);
6. площади петель QRS и T;
7. вектор полуплощади (вектор, который делит ВКГ- петлю на две части, равные по площади);
8. время переднего и заднего отклонения петли QRS в горизонталь-ной и сагиттальной плоскостях, верхнего и нижнего отклонения во фронтальной плоскости;
9. направление вращения петель QRS и T при формировании пе-тель;
При анализе пространственных показателей ВКГ определяют:
1. максимальный модуль вектора в каждом из восьми октантов векторкардиографической системы координат;
2. интервалы времени пребывания вектора в определенных октантах;
3. степень отклонения формы ВКГ- петли от плоской, или ее изогну-тости;
4. пространственную скорость конца вектора сердца и угловую ско-рость вектора;
5. скорость изменения площади поверхности, ометаемой вектором;
6. истинную площадь пространственной ВКГ- петли.
Векторкардиографическое исследование проводятся по следую-щим показаниям:
1. ранняя диагностика гипертрофии миокарда желудочков и пред-сердий.
2. диагностика гипертрофии желудочка на фоне блокады правой ножки пучка Гиса.
3. диагностика комбинированной гипертрофии желудочков.
4. наличие полифазных комплексов QRS в правых грудных отведе-ниях.
5. инфаркты миокарда задней локализации.
6. мало измененная или нетипично измененная ЭКГ при несом-ненном заболевании сердца.
7. трудно интерпретируемые изменения предсердного и желудочко-вого комплексов ЭКГ.
Средние величины показателей векторкардиограммы здоровых людей.
В таблицах 3 и 4 приведены показатели ВКГ здоровых лиц, полученные Франком.
Таблица 3
Плоскостные показатели ВКГ (на основании исследования 100 здоровых)
| Наименование значений | Горизонтальная плоскость | Фронтальная плоскость | Сагиттальная плоскость |
| Максимальный вектор петли QRS, мВ | 1,12 ± 0,21 | 1,18 ± 0,15 | 1,16 ± 0,12 |
| Направление вектора петли QRS, градусы | 335 ± 30 | 42,3 ± 7,2 | 5,35 ± 22,3 |
| Максимальный вектор петли Т, мВ | 0,58 ± 0,18 | 0,46 ± 0,11 | 0,52 ± 0,12 |
| Направление вектора петли Т, градусы | 52 ± 12,5 | 36,2 ± 10,1 | 146,3 ± 30,2 |
| Моментные векторы, градусы | Горизонтальная плоскость | Фронтальная плоскость | Сагиттальная плоскость |
| 0,01с | 120 ± 41 | 152 ± 72 | 192 ± 50 |
| 0,02с | 54 ± 25 | 40 ± 53 | 150 ± 38 |
| 0,03с | 12 ± 12 | 36 ± 12 | 146 ± 22 |
| 0,04с | 355 ± 20 | 46 ± 18 | 92 ± 16 |
Одной из популярных форм представления ЭКГ- данных является векторкардиограмма (ВКГ) в трех ортогональных проекциях - фронтальной, левой сагитальной и горизонтальной (F, Sl и Н), построенная по ортогональным или квазиортогональным (I, aVF и - V2) ЭКГ - отведениям.
Таблица 4
Пространственные показатели ВКГ (на основании 100 здоровых пациентов)
| Наименование значений | Величины |
| Максимальный пространственный вектор петли QRS, мВ | 1,42 ± 0,25 |
| Максимальный пространственный вектор петли Т, мВ | 0,58 ± 0,22 |
| Пространственный угол QRS-T, градусы | 68,7 ± 24,6 |
| Азимут, градусы | 392,4 ± 35,3 |
| Угол подъема, градусы | 50,4 ± 16,2 |
Дата добавления: 2016-04-06; просмотров: 4558;
