Нормальный закон распределения наработки до отказа
Нормальное распределение вероятности безотказной работы описывает схему длительного «естественного» старения (постепенные отказы). В этом случае отказы являются следствием накопления повреждений:
– при постоянной скорости износа;
– однородном начальном качестве объектов.
При таких начальных условиях большая часть отказов наблюдается в течение конечного периода работы объекта.
Нормальное распределение, или распределение Гаусса, является наиболее универсальным, удобным и широко применимым.
Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы.
Нормальному распределению подчиняются наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий, размеры, ошибки измерения деталей и т. д.
Плотность распределения отказов описывается формулой
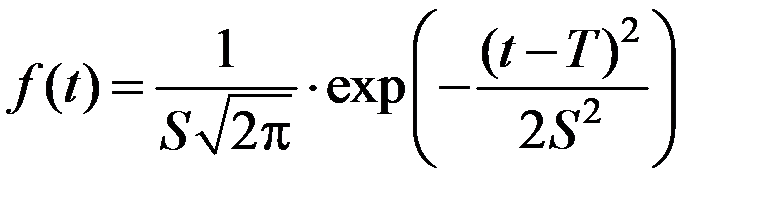 . (4.9)
. (4.9)
Распределение имеет два независимых параметра: математическое ожидание mt и среднее квадратическое отклонение S.
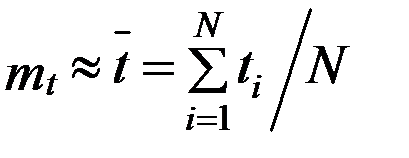 , (4.10)
, (4.10)
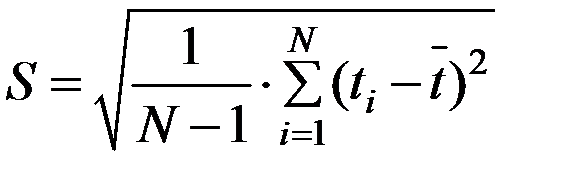 . (4.11)
. (4.11)
Графики изменения показателей безотказности при нормальном распределении приведены на рис. 4.5.
Выясним смысл параметров Т и S нормального распределения. Из графика f(t) видно, что Т является центром симметрии распределения, поскольку при изменении знака разности (t – Т) выражение (4.9) не меняется. При t = Т функция f(t) достигает своего максимума:
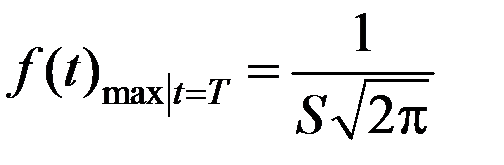 . (4.12)
. (4.12)
| f(t) λ(t) |
| λ(t) |
| P(t) |
| f(t) |
| t |
Рис. 4.5. Графики функций показателей безотказности при нормальном распределении
Параметр S характеризует форму кривой f(t), т. е. рассеивание случайной величины T. Кривая плотности распределения f(t) тем выше и острее, чем меньше S. Она начинается от t = –∞ и распространяется до t = ∞. Это не является существенным недостатком, если T ≥ 3S, так как площадь, очерченная уходящими в бесконечность ветвями кривой плотности, очень мала. Так, вероятность отказа за период времени до Т = –3S составляет всего 0,135 % и обычно не учитывается в расчетах. Наибольшая ордината кривой плотности распределения равна 0,399/S (рис. 4.6).
| f(t) |
| 0,399/S S S < S1 S1 |
| 3S 2S S 0 S 2S 3S t |
| P(t) |
| S S < S1 S1 S1 |
| 0 3S2SS 0 S 2S 3S t |
а) б)
Рис. 4.6. Функция плотности вероятности (а) и интегральная функция
вероятности нормального распределения (б)
Вероятность отказа при таком распределении определяется интегральной функцией
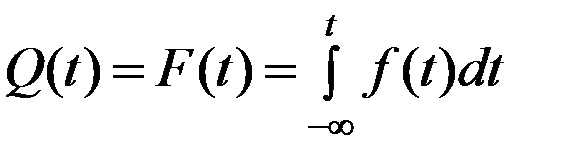 . (4.13)
. (4.13)
Вероятность безотказной работы
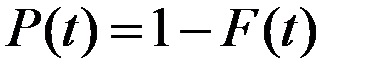 , (4.14)
, (4.14)
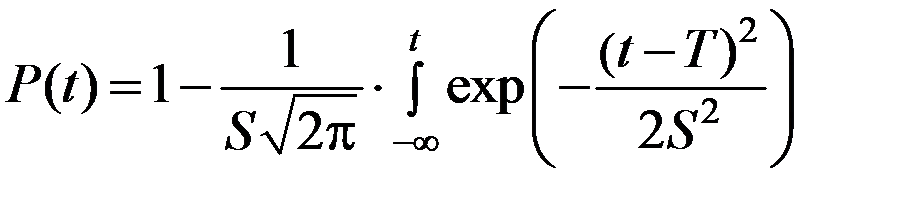 . (4.15)
. (4.15)
Вычисление интегралов заменяют использованием таблиц значений P(t) в зависимости от квантили нормированного нормального распределения
(табл. 4.2):
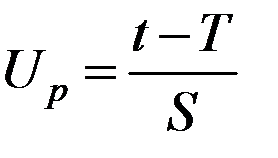 . (4.16)
. (4.16)
Помимо прямой задачи, т. е. оценки вероятности безотказной работы за данную наработку, зачастую требует решения обратное определение наработки, соответствующей заданной вероятности безотказной работы.
Значение этой наработки определяют также с помощью квантили:
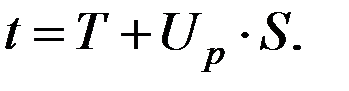 (4.17)
(4.17)
Таблица 4.2
Дата добавления: 2016-02-16; просмотров: 2967;
