Гамма-распределение
Гамма-распределение времени безотказной работы описывает схему непрерывного, постепенного износа, при котором отказ не наступает вследствие первого же повреждения, а является следствием накопления повреждений. Каждое из этих повреждений происходит по схеме мгновенного повреждения.
Граничными условиями применения гамма-распределения являются следующие:
– средняя скорость износа устройства постоянна;
– средняя скорость износа подвержена случайным вариациям;
– начальное качество исследуемых устройств полностью однородно.
Случайная величина наработки до отказа T имеет гамма-распределение с параметрами α (масштабный параметр) и β (параметр формы), где 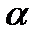 ,
, 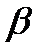 > 0, причём
> 0, причём 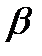 – целое число, если функция плотности распределения описывается выражением:
– целое число, если функция плотности распределения описывается выражением:
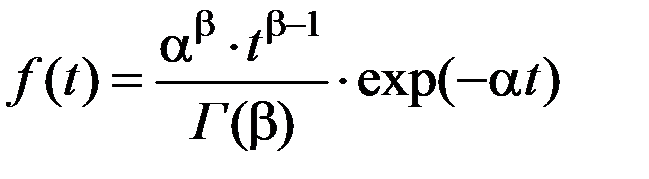 , (4.29)
, (4.29)
где Г( 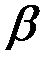 ) = (
) = ( 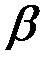 – 1)! – гамма-функция Эйлера.
– 1)! – гамма-функция Эйлера.
Очевидно, что при 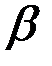 = 1 выражение (4.29) упрощается до вида
= 1 выражение (4.29) упрощается до вида 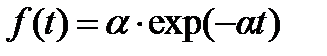 , соответствующего экспоненциальному распределению.
, соответствующего экспоненциальному распределению.
Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону.
При больших значениях 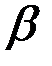 гамма-распределение сходится к нормальному распределению с параметрами:
гамма-распределение сходится к нормальному распределению с параметрами: 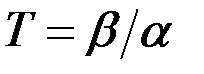 ,
, 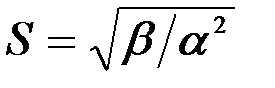 .
.
Графики изменения показателей надежности при гамма-распределении приведены на рис. 4.10.
Числовые характеристики наработки до отказа:
– средняя наработка (математическое ожидание наработки) до отказа
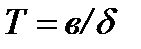 ,(4.30)
,(4.30)
– дисперсия наработки до отказа
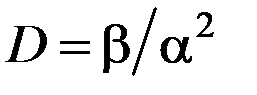 . (4.31)
. (4.31)
| P(t) |
| λ(t) |
| f(t) |
| 0 t |
| P(t) f(t) λ(t) 1 |
Рис. 4.10. Графики изменения показателей надежности при гамма-распределении
Дата добавления: 2016-02-16; просмотров: 798;
