Линии 2 порядка на проективной плоскости
Приведение уравнения линии 2 порядка к каноническому виду. Квадрики.
Некоторые свойства линий 2 порядка на проективной плоскости в модели пополненной плоскости.
Теоремы Паскаля и Брианшона.
Проективные преобразования проективных пространств
Перспективные соответствия проективных прямых, проективных плоскостей. Некоторые инварианты при перспективных соответствиях.
Проективные преобразования и отображения проективных пространств: различные определения и их эквивалентность. Проективные преобразования в координатах.
Группа проективных преобразований и ее подгруппы. Проективно-аффинные преобразования.
Проективная классификация линий 2 порядка относительно группы проективных преобразований. Связь с аффинной классификацией.
Приложение проективной геометрии к решению задач элементарной геометрии
Схема решения задач элементарной геометрии методами проективной геометрии.
Примеры задач, решаемых методами проективной геометрии.
Практические задания с решениями
Решаемые задачи иллюстрируют лекционный курс, а также создают мотивацию к последующему изучению теоретического материала. Четкая запись условий задач, подробная, структурированная запись решения геометрических задач является основным требованием к работе как преподавателя, так и студентов, что необходимо для качественного объяснения и усвоения геометрического материала. Недопустимы «приблизительные» решения, а также их отсутствие (только чертеж), что создает иллюзию понимания.
Тема 1. Сравнительное изложение аффинной и евклидовой геометрий
Список необходимых сведений:определения аффинных преобразований и движений аффинного и евклидова пространства. Их свойства.
Практические задания
1. На плоскости относительно прямоугольной системы координат дано каноническое уравнение эллипса с параметрами a , b.Перевести аффинным преобразованием данный эллипсв единичную окружность с центром в начале координат.
Решение.
Каноническое уравнение эллипса 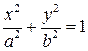 .
.
Перепишем его в виде 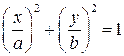 .
.
Рассмотрим аффинное преобразование 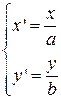 .
.
Оно переводит эллипс в единичную окружность с уравнением 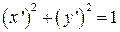 .
.
Штрихи над координатами x и y показывают, что единичная окружность является образом. После того как уравнение образа получено, то штрихи можно не писать.
2. На плоскости относительно прямоугольной системы координат даны две единичные окружности: с центром в начале координат и с центром в точке 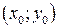 .Перевести одну окружность в другую аффинным преобразованием.
.Перевести одну окружность в другую аффинным преобразованием.
Решение.
Рассмотрим две единичные окружности
 и
и 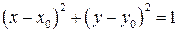 .
.
Рассмотрим движение  . Оно является параллельным переносом на вектор с координатами
. Оно является параллельным переносом на вектор с координатами 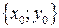 и переводит первую окружность во вторую.
и переводит первую окружность во вторую.
3. Можно ли перевести любой эллипс в любой эллипс движением плоскости и почему?
Решение.
Из задач 1, 2 вытекает, что аффинным преобразованием можно перевести любой эллипс в любой эллипс. Для этого надо перевести оба эллипса в единичные окружности с теми же центрами, а затем перевести окружности друг в друга. Однако в случае произвольных канонических параметров эллипсов этого нельзя добиться движением, так как параметры отвечают за размеры эллипсов.
4. Можно ли перевести эллипс в гиперболу (или любую другую кривую 2 порядка) аффинным преобразованием и почему?
Решение.
Невозможно перевести аффинным преобразованием эллипс в гиперболу, так как эти фигуры имеют различные инвариантные свойства. В частности, эллипс является ограниченной фигурой, а гипербола – неограниченной. Эллипс не имеет асимптот, а гипербола имеет.
Аналогичные задачи надо уметь решать для всех кривых 2 порядка на плоскости.
Сделать следующие выводы.
Любой эллипс можно перевести в любой эллипс аффинным преобразованием.
Два эллипса можно перевести друг в друга движением плоскости только если они имеют одинаковые канонические параметры.
Сделать аналогичные выводы для других кривых 2 порядка на плоскости.
Составить список инвариантных (относительно аффинных преобразований) свойств и показать, что кривые из разных канонических классов имеют разные инвариантные свойства. Следовательно, не могут быть переведены друг в друга аффинным преобразованием.
Дата добавления: 2016-03-27; просмотров: 1596;
