Задачи с решениями по всему курсу.
Задача 1. Выяснить тип инволюции:
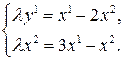

Решение. Пусть 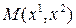 – инвариантная точка инволюции. Тогда
– инвариантная точка инволюции. Тогда
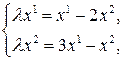 или
или 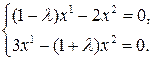
Откуда получаем, что
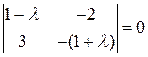 , или
, или 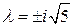 .
.
Так как 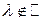 , то получаем, что инволюция не имеет неподвидных точек, т.е. является эллиптической.
, то получаем, что инволюция не имеет неподвидных точек, т.е. является эллиптической.
Задача 2. Вычислить координаты инвариантных точек инволюции:
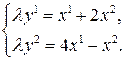
Решение. Пусть 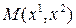 – инвариантная точка инволюции. Тогда
– инвариантная точка инволюции. Тогда
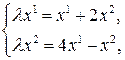 или
или 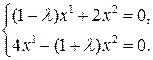
Система совместна если и только если
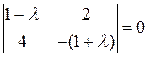 .
.
Решая уравнение 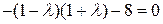 , получаем
, получаем 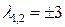 . Подставляя
. Подставляя 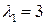 в первое уравнение, имеем
в первое уравнение, имеем 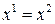 , т.е.
, т.е. 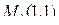 – инвариантная точка. Аналогично, подставляя
– инвариантная точка. Аналогично, подставляя 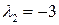 в первое уравнение, получаем
в первое уравнение, получаем  , т.е.
, т.е. 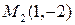 – инвариантная точка инволюции.
– инвариантная точка инволюции.
Задача 3. Гомология 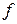 задана центром
задана центром 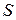 , осью
, осью 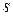 и точками
и точками 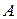 и
и 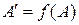 . Построить:
. Построить:
1) точку 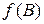 , где
, где 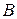 – данная точка прямой
– данная точка прямой 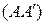 ;
;
2) точку 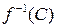 , где
, где 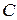 – данная точка;
– данная точка;
3) точку 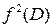 , где
, где 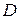 – данная точка.
– данная точка.
Решение. 1) Возьмем произвольную точку 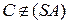 ,
, 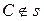 и построим
и построим 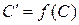 :
: 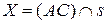 ,
, 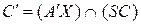 . Далее, пользуясь соответственными точками
. Далее, пользуясь соответственными точками 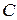 и
и 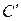 , строим
, строим 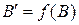 .
.
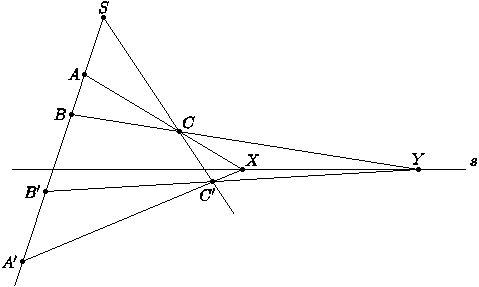
Рис 42
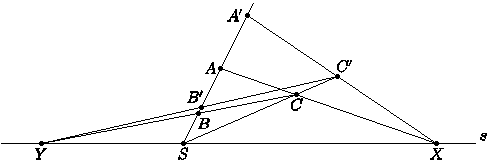
Рис 43
Задача 4. Написать формулы проективного преобразования 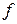 прямой по трем парам соответствующих точек:
прямой по трем парам соответствующих точек: 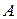 и
и 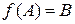 ,
, 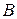 и
и 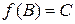 ,
, 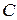 и
и 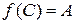 , если
, если 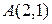 ,
, 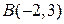 ,
, 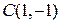 .
.
Решение. Пусть 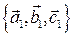 – система векторов, согласованная относительно репера
– система векторов, согласованная относительно репера 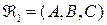 , т.е.
, т.е. 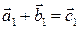 и векторы
и векторы 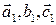 порождают соответственно точки
порождают соответственно точки 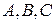 . Решив систему уравнений
. Решив систему уравнений
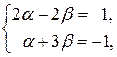 получаем
получаем 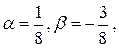 т.е.
т.е. 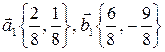 .
.
Пусть 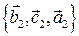 – система векторов, согласованная относительно репера
– система векторов, согласованная относительно репера 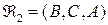 , т.е.
, т.е. 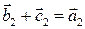 и векторы
и векторы 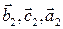 порождают соответственно точки
порождают соответственно точки  . Решая систему уравнений
. Решая систему уравнений
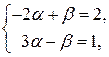 получаем
получаем 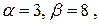 т.е.
т.е. 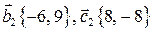 .
.
В проективном преобразовании прямой 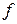 репер
репер 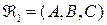 переходит в репер
переходит в репер 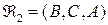 , поэтому
, поэтому
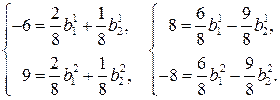
Решив системы уравнений, получаем формулы проективного преобразования прямой:

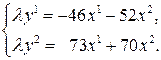
Задача 5. (Задача о бабочке). Через внутреннюю точку O эллипса проведены три хорды [AB], [MN], [PQ]. Точка О является серединой хорды [AB], которая пересекает отрезки [PM] и [NQ] соответственно в точках E и F. Доказать, что точка О есть середина отрезка [EF].
Проективное решение.
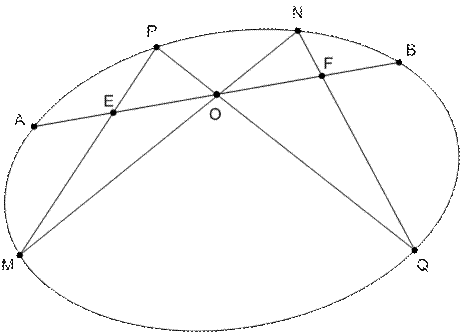
Рис. 44
Рассмотрим перспективное отображение прямой (АВ) в пучёк прямых, проходящих через точку М, далее, согласно конструкции Штейнера, отображаем прямые, проходящие через точку М в пучёк прямых, проходящих через точку Q, которые в свою очередь снова отображаем перспективно на прямую (АВ). В результате точка Е перейдет в точку О, точка О – в точку F, точки А и В останутся неподвижными. Произведем симметрию относительно точки О. Точка F перейдет в некоторую точку G. При проективных преобразованиях сложное отношение четырёх точек, лежащих на одной прямой, сохраняется, то есть (АВ,ОЕ) = (ВА, GO) =(AB,OG). Таким образом, Е=G. Cледовательно, точка О есть середина отрезка [EF].
Для сравнения рассмотрим классическое доказательство теоремы о бабочке в круге методами евклидовой геометрии.
Теорема о бабочке. Пусть через точку  , являющуюся серединой хорды
, являющуюся серединой хорды 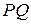 некоторой окружности, проведены две произвольные хорды
некоторой окружности, проведены две произвольные хорды 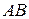 и
и 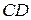 . Хорды
. Хорды 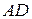 и
и 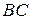 пересекают отрезок
пересекают отрезок 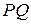 в точках
в точках  и
и 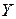 . Тогда точка
. Тогда точка  является серединой отрезка
является серединой отрезка  .
.
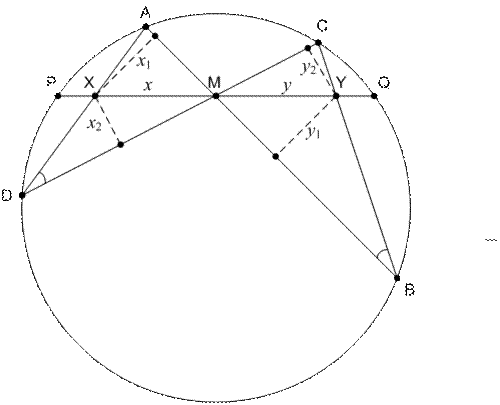
Рис. 45
Доказательство. Опустим перпендикуляры 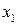 и
и 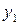 из точек
из точек  и
и 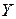 на прямую
на прямую 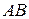 , затем перпендикуляры
, затем перпендикуляры 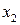 и
и 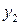 из точек
из точек  и
и 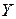 на прямую
на прямую 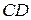 . Введем обозначения:
. Введем обозначения: 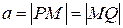 ,
, 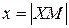 ,
, 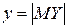 ,
, 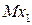 – треугольник с вершиной
– треугольник с вершиной  и противолежащей ей стороной
и противолежащей ей стороной 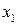 , аналогично и для других треугольников. Из рассмотрения пар подобных треугольников
, аналогично и для других треугольников. Из рассмотрения пар подобных треугольников 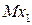 и
и 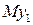 ,
,  и
и 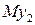 ,
, 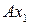 и
и 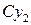 ,
, 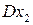 и
и 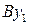 вытекает, что
вытекает, что
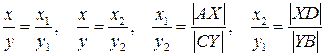 ,
,
откуда
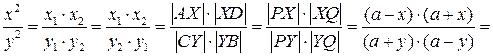
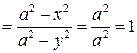 и
и  , что и требовалось доказать.
, что и требовалось доказать.
Задача 6. Центр инволютивной гомологии имеет координаты 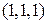 , а ось гомологии – уравнение
, а ось гомологии – уравнение 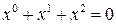 . Написать формулы преобразования.
. Написать формулы преобразования.
Решение. Пусть 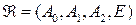 ,
, 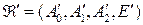 , где
, где 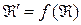 . Прямая
. Прямая 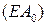 имеет уравнение
имеет уравнение 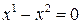 . Точка
. Точка 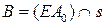 , где
, где 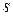 – ось гомологии имеет координаты
– ось гомологии имеет координаты  . Так как
. Так как 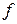 – инволютивная гомология, то
– инволютивная гомология, то 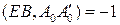 . Пусть
. Пусть 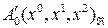 . Проектируем точки
. Проектируем точки 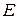 ,
, 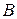 ,
, 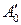 из центра
из центра 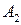 на прямую
на прямую 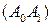 . Получаем:
. Получаем: 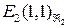 ,
, 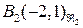 ,
, 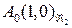 ,
, 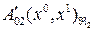 .
.
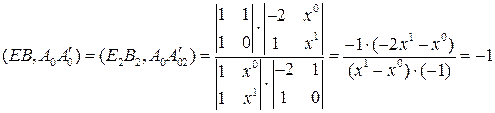 ,
,
откуда 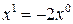 . Так как
. Так как 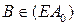 , то
, то 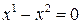 . Получаем, что
. Получаем, что 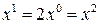 , т.е.
, т.е. 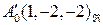 .
.
Аналогично находим 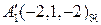 ,
, 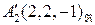 .
.  , т.к.
, т.к. 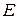 – центр гомологии. Матрица перехода от
– центр гомологии. Матрица перехода от 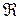 к
к 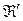 имеет вид:
имеет вид:

Согласовываем столбцы матрицы перехода, решая систему линейных уравнений
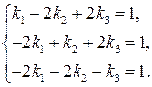
Получаем 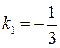 ,
, 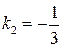 ,
, 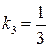 . Согласованная матрица перехода имеет вид:
. Согласованная матрица перехода имеет вид:
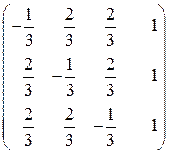 .
.
Получаем аналитическое выражение заданной инволютивной гомологии:
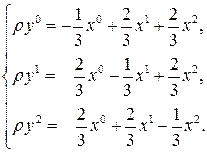 или
или 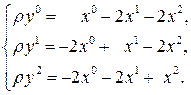
Задача 7. Доказать теорему:
Если 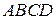 – полный четырехвершинник с вершинами на овальной кривой второго порядка, то каждая его диагональная точка является полюсом противолежащей диагонали.
– полный четырехвершинник с вершинами на овальной кривой второго порядка, то каждая его диагональная точка является полюсом противолежащей диагонали.
Решение. Докажем, например, что  является полюсом противолежащей диагонали
является полюсом противолежащей диагонали 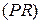 , т.е.
, т.е. 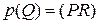 . Остальное доказывается аналогично. По теореме о гармонических свойствах полного четырехвершинника
. Остальное доказывается аналогично. По теореме о гармонических свойствах полного четырехвершинника 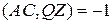 ,
,  . Отсюда следует, что
. Отсюда следует, что 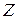 и
и 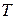 гармонически сопряжены с точкой
гармонически сопряжены с точкой  относительно овальной кривой и, следовательно, лежат на ее поляре. Поэтому
относительно овальной кривой и, следовательно, лежат на ее поляре. Поэтому  .
.
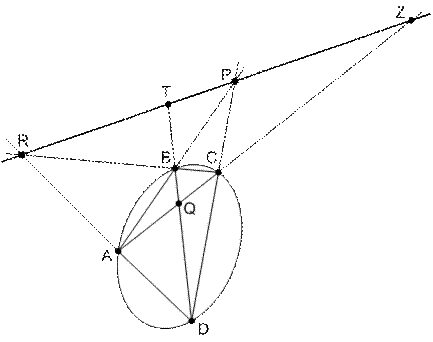
Рис. 46
Задача 8. Даны овальная кривая второго порядка  и точка
и точка  . Построить поляру точки
. Построить поляру точки  , если:
, если:
1)  – внешняя точка относительно
– внешняя точка относительно  ;
;
2)  – внутренняя точка относительно
– внутренняя точка относительно  ;
;
3) 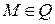 .
.
Решение.
1) Через  проведем три секущие, пересекающие овальную кривую в точках
проведем три секущие, пересекающие овальную кривую в точках 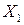 ,
, 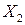 ,
, 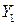 ,
, 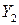 ,
,  ,
, 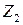 . Пусть
. Пусть 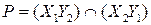 ,
, 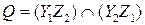 . Так как
. Так как 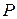 и
и  лежат на поляре точки
лежат на поляре точки  , то
, то 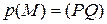 .
.
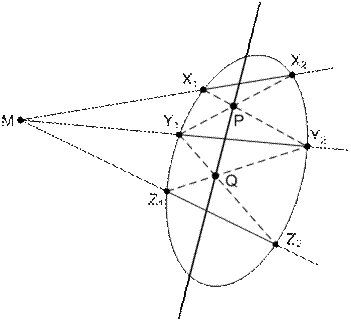
Рис. 47
2) Через  проведем две произвольные прямые, пересекающие овальную кривую в точках
проведем две произвольные прямые, пересекающие овальную кривую в точках 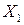 ,
, 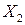 ,
, 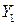 ,
, 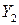 . Пусть
. Пусть 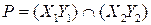 ,
, 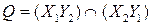 . На основании теоремы, доказанной в предыдущей задаче, делаем вывод, что
. На основании теоремы, доказанной в предыдущей задаче, делаем вывод, что 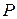 и
и  лежат на поляре точки
лежат на поляре точки  , т.е.
, т.е. 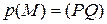 .
.
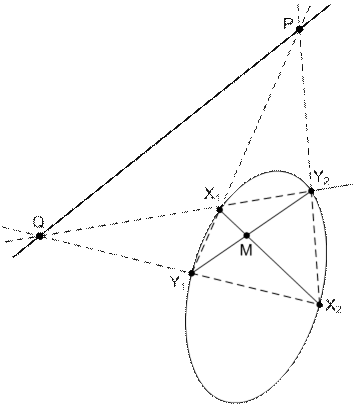
Рис. 48
3) Проводим через  секущую
секущую  и строим ее полюс
и строим ее полюс 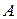 . Тогда
. Тогда 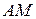 будет искомой касательной. Возьмем две внутренние точки
будет искомой касательной. Возьмем две внутренние точки 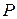 и
и  на прямой
на прямой  и построим их поляры
и построим их поляры 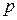 и
и  . Тогда
. Тогда 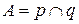 и
и  – касательная.
– касательная.
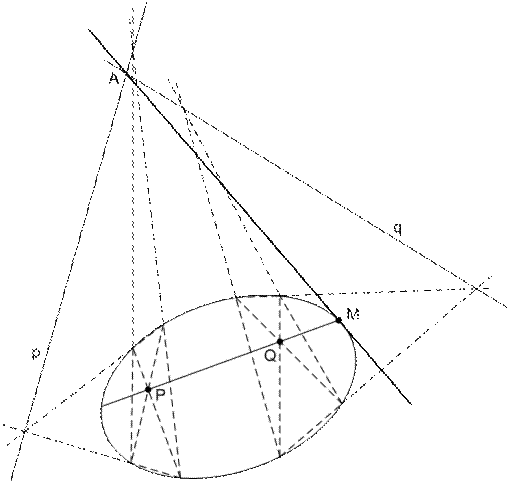
Рис. 49
Задача 9. Построить полюс данной прямой 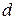 относительно данной овальной кривой второго порядка
относительно данной овальной кривой второго порядка  .
.
Решение. Возьмем две точки 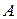 и
и 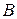 на прямой
на прямой 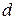 и построим их поляры
и построим их поляры  и
и  . Тогда
. Тогда 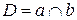 будет полюсом прямой
будет полюсом прямой 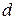 .
.
Задача 10. Из данной точки  евклидовой плоскости провести касательную к данной окружности
евклидовой плоскости провести касательную к данной окружности  с помошью одной линейки.
с помошью одной линейки.
Указание. а) если 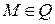 , то поляра
, то поляра 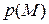 точки
точки  будет искомой касательной.
будет искомой касательной.
б) в случае 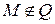 касательными будут
касательными будут 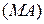 и
и 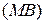 , где
, где 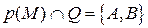 .
.
Задача 11. Точка 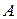 – внешняя относительно окружности
– внешняя относительно окружности  с центром
с центром 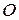 . Через точку
. Через точку 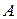 проведены всевозможные секущие к окружности
проведены всевозможные секущие к окружности  , отличные от прямой
, отличные от прямой 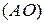 . Доказать, что точки пересечения касательных к окружности
. Доказать, что точки пересечения касательных к окружности  в точках ее пересечения с каждой секущей лежат на одной прямой, перпендикулярной к прямой
в точках ее пересечения с каждой секущей лежат на одной прямой, перпендикулярной к прямой 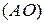 .
.
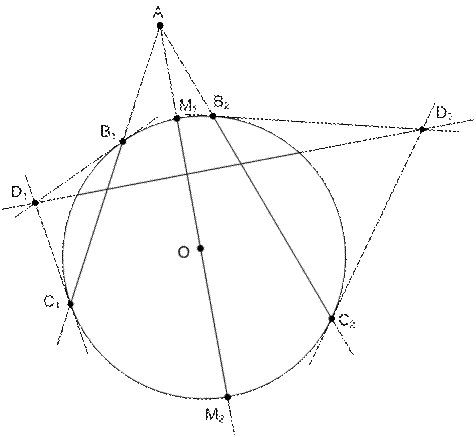
Рис. 50
Решение. Точка 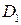 является полюсом для
является полюсом для 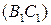 . Поляра точки
. Поляра точки 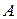 проходит через
проходит через 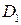 , так как
, так как 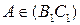 , т.е
, т.е  . Аналогично,
. Аналогично, 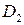 является полюсом для
является полюсом для 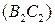 и поляра точки
и поляра точки 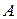 проходит через
проходит через 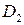 , так как
, так как 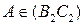 , т.е
, т.е 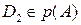 . Получили, что
. Получили, что 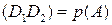 . Так как точки
. Так как точки 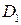 и
и 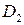 взяты произвольно, то всякая точка
взяты произвольно, то всякая точка 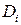 , являющаяся точкой пересечения касательных к окружности
, являющаяся точкой пересечения касательных к окружности  в точках ее пересечения с секущей, будет принадлежать поляре точки
в точках ее пересечения с секущей, будет принадлежать поляре точки 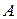 , т.е.
, т.е. 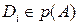 . Пусть
. Пусть 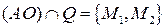 . По свойству окружности касательные в точках
. По свойству окружности касательные в точках 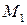 и
и 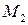 к
к  перпендикулярны
перпендикулярны 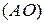 и пересекаются в несобственной точке
и пересекаются в несобственной точке 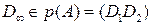 . Поэтому
. Поэтому  .
.
Задача 12. В окружности  проведены параллельные хорды и в их концах – касательные к окружности. Доказать, что точки пересечения касательных в концах каждой из хорд лежат на одной прямой, перпендикулярной этим хордам и проходящей через центр окружности
проведены параллельные хорды и в их концах – касательные к окружности. Доказать, что точки пересечения касательных в концах каждой из хорд лежат на одной прямой, перпендикулярной этим хордам и проходящей через центр окружности  .
.
Указание. Сводится к задаче 11, когда 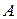 является несобственной точкой. Остается лишь показать, что
является несобственной точкой. Остается лишь показать, что 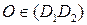 . Пусть
. Пусть 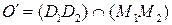 . Тогда
. Тогда 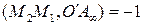 , так как
, так как 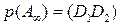 , откуда следует, что
, откуда следует, что 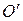 – середина отрезка
– середина отрезка 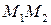 и
и 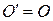 (
( 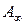 – несобственная точка прямой
– несобственная точка прямой 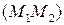 ).
).
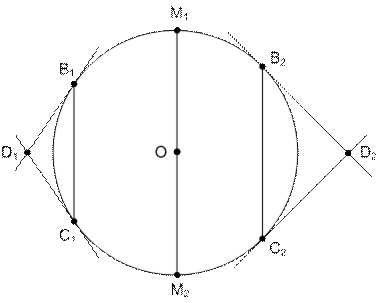
Рис. 51
Задача 13. Овальная кривая второго порядка задана тремя своими точками и касательными в двух из них. Построить:
1) касательную в третьей точке;
2) еще одну точку кривой.
Решение. Используем предельный случай теоремы Паскаля. Пусть 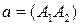 , где
, где 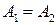 ,
, 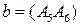 , где
, где 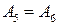 – заданные касательные.
– заданные касательные.
1) Построим касательную в третьей точке, т.е. прямую 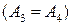 , где
, где 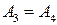 . Строим
. Строим 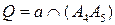 ,
, 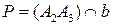 ,
, 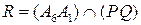 . Прямая
. Прямая 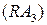 – искомая касательная.
– искомая касательная.
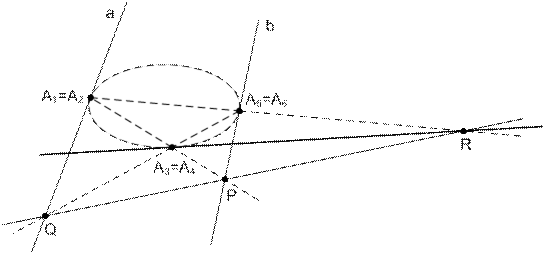
Рис. 52
2) Построим точку 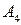 . Пусть
. Пусть 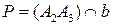 . Проводим через
. Проводим через 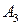 произвольную прямую
произвольную прямую 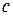 , не проходящую через
, не проходящую через 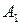 и
и 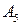 , и пусть
, и пусть  . Строим
. Строим 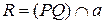 и
и 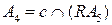 .
.
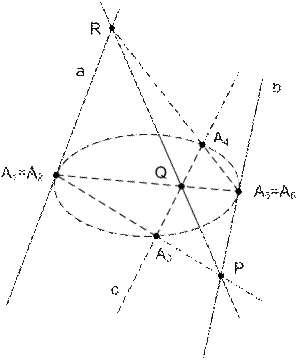
Рис. 53
Задача 14. Центр инволютивной гомологии имеет координаты 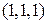 , а ось гомологии – уравнение
, а ось гомологии – уравнение 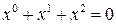 . Написать формулы преобразования.
. Написать формулы преобразования.
Решение. Пусть 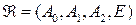 ,
, 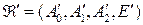 , где
, где 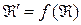 . Прямая
. Прямая 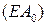 имеет уравнение
имеет уравнение 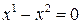 . Точка
. Точка 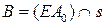 , где
, где 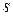 – ось гомологии имеет координаты
– ось гомологии имеет координаты  . Так как
. Так как 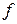 – инволютивная гомология, то
– инволютивная гомология, то 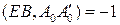 . Пусть
. Пусть 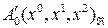 . Проектируем точки
. Проектируем точки 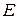 ,
, 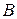 ,
, 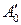 из центра
из центра 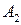 на прямую
на прямую 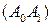 . Получаем:
. Получаем: 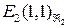 ,
, 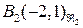 ,
, 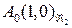 ,
, 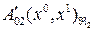 .
.
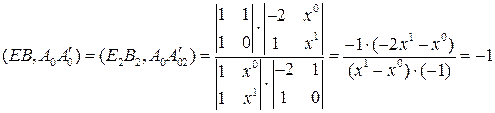 ,
,
откуда 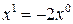 . Так как
. Так как 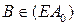 , то
, то 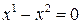 . Получаем, что
. Получаем, что 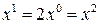 , т.е.
, т.е. 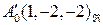 .
.
Аналогично находим 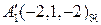 ,
, 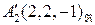 .
.  , т.к.
, т.к. 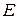 – центр гомологии. Матрица перехода от
– центр гомологии. Матрица перехода от 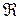 к
к 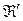 имеет вид:
имеет вид:

Согласовываем столбцы матрицы перехода решая систему линейных уравнений
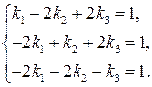
Получаем 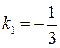 ,
, 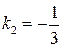 ,
, 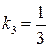 . Согласованная матрица перехода имеет вид:
. Согласованная матрица перехода имеет вид:
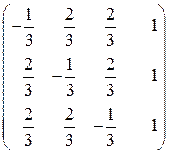 .
.
Получаем аналитическое выражение заданной инволютивной гомологии:
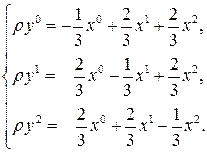 или
или 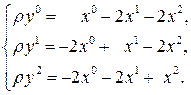
Задача 15. Доказать теорему:
Если 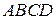 – полный четырехвершинник с вершинами на овальной кривой второго порядка, то каждая его диагональная точка является полюсом противолежащей диагонали.
– полный четырехвершинник с вершинами на овальной кривой второго порядка, то каждая его диагональная точка является полюсом противолежащей диагонали.
Решение. Докажем, например, что  является полюсом противолежащей диагонали
является полюсом противолежащей диагонали 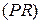 , т.е.
, т.е. 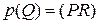 . Остальное доказывается аналогично. По теореме о гармонических свойствах полного четырехвершинника
. Остальное доказывается аналогично. По теореме о гармонических свойствах полного четырехвершинника 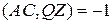 ,
,  . Отсюда следует, что
. Отсюда следует, что 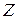 и
и 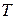 гармонически сопряжены с точкой
гармонически сопряжены с точкой  относительно овальной кривой и, следовательно, лежат на ее поляре. Поэтому
относительно овальной кривой и, следовательно, лежат на ее поляре. Поэтому  .
.

Рис. 54
Задача 16. Даны овальная кривая второго порядка  и точка
и точка  . Построить поляру точки
. Построить поляру точки  , если:
, если:
1)  – внешняя точка относительно
– внешняя точка относительно  ;
;
2)  – внутренняя точка относительно
– внутренняя точка относительно  ;
;
3) 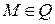 .
.
Решение.
1) Через  проведем три секущие, пересекающие овальную кривую в точках
проведем три секущие, пересекающие овальную кривую в точках 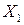 ,
, 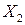 ,
, 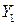 ,
, 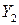 ,
,  ,
, 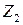 . Пусть
. Пусть 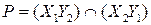 ,
, 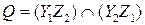 . Так как
. Так как 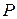 и
и  лежат на поляре точки
лежат на поляре точки  , то
, то 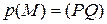 .
.

Рис. 55
2) Через  проведем две произвольные прямые, пересекающие овальную кривую в точках
проведем две произвольные прямые, пересекающие овальную кривую в точках 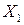 ,
, 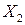 ,
, 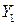 ,
, 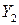 . Пусть
. Пусть 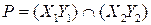 ,
, 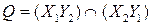 . На основании теоремы, доказанной в предыдущей задаче, делаем вывод, что
. На основании теоремы, доказанной в предыдущей задаче, делаем вывод, что 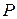 и
и  лежат на поляре точки
лежат на поляре точки  , т.е.
, т.е. 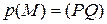 .
.

Рис. 56
3) Проводим через  секущую
секущую  и строим ее полюс
и строим ее полюс 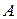 . Тогда
. Тогда 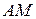 будет искомой касательной. Возьмем две внутренние точки
будет искомой касательной. Возьмем две внутренние точки 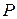 и
и  на прямой
на прямой  и построим их поляры
и построим их поляры 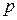 и
и  . Тогда
. Тогда 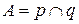 и
и  – касательная.
– касательная.

Рис. 57
Задача 17. Построить полюс данной прямой 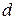 относительно данной овальной кривой второго порядка
относительно данной овальной кривой второго порядка  .
.
Решение. Возьмем две точки 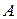 и
и 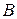 на прямой
на прямой 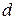 и построим их поляры
и построим их поляры  и
и  . Тогда
. Тогда 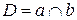 будет полюсом прямой
будет полюсом прямой 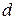 .
.
Задача 18. Из данной точки  евклидовой плоскости провести касательную к данной окружности
евклидовой плоскости провести касательную к данной окружности  с помошью одной линейки.
с помошью одной линейки.
Указание. а) если 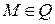 , то поляра
, то поляра 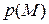 точки
точки  будет искомой касательной.
будет искомой касательной.
б) в случае 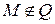 касательными будут
касательными будут 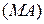 и
и 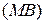 , где
, где 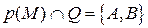 .
.
Задача 19. Точка 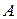 – внешняя относительно окружности
– внешняя относительно окружности  с центром
с центром 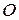 . Через точку
. Через точку 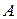 проведены всевозможные секущие к окружности
проведены всевозможные секущие к окружности  , отличные от прямой
, отличные от прямой 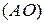 . Доказать, что точки пересечения касательных к окружности
. Доказать, что точки пересечения касательных к окружности  в точках ее пересечения с каждой секущей лежат на одной прямой, перпендикулярной к прямой
в точках ее пересечения с каждой секущей лежат на одной прямой, перпендикулярной к прямой 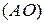 .
.

Рис. 58
Решение. Точка 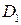 является полюсом для
является полюсом для 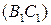 . Поляра точки
. Поляра точки 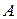 проходит через
проходит через 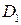 , так как
, так как 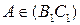 , т.е
, т.е  . Аналогично,
. Аналогично, 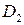 является полюсом для
является полюсом для 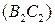 и поляра точки
и поляра точки 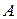 проходит через
проходит через 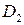 , так как
, так как 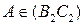 , т.е
, т.е 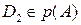 . Получили, что
. Получили, что 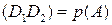 . Так как точки
. Так как точки 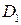 и
и 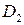 взяты произвольно, то всякая точка
взяты произвольно, то всякая точка 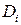 , являющаяся точкой пересечения касательных к окружности
, являющаяся точкой пересечения касательных к окружности  в точках ее пересечения с секущей, будет принадлежать поляре точки
в точках ее пересечения с секущей, будет принадлежать поляре точки 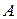 , т.е.
, т.е. 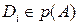 . Пусть
. Пусть 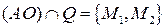 . По свойству окружности касательные в точках
. По свойству окружности касательные в точках 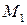 и
и 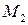 к
к  перпендикулярны
перпендикулярны 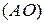 и пересекаются в несобственной точке
и пересекаются в несобственной точке 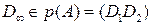 . Поэтому
. Поэтому  .
.
Задача 20. В окружности  проведены параллельные хорды и в их концах – касательные к окружности. Доказать, что точки пересечения касательных в концах каждой из хорд лежат на одной прямой, перпендикулярной этим хордам и проходящей через центр окружности
проведены параллельные хорды и в их концах – касательные к окружности. Доказать, что точки пересечения касательных в концах каждой из хорд лежат на одной прямой, перпендикулярной этим хордам и проходящей через центр окружности  .
.
Указание. Сводится к задаче 11, когда 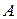 является несобственной точкой. Остается лишь показать, что
является несобственной точкой. Остается лишь показать, что 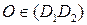 . Пусть
. Пусть 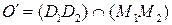 . Тогда
. Тогда 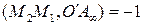 , так как
, так как 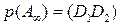 , откуда следует, что
, откуда следует, что 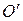 – середина отрезка
– середина отрезка 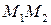 и
и 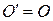 (
( 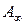 – несобственная точка прямой
– несобственная точка прямой 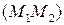 ).
).

Рис. 59
Задача 21. Овальная кривая второго порядка задана тремя своими точками и касательными в двух из них. Построить:
3) касательную в третьей точке;
4) еще одну точку кривой.
Решение. Используем предельный случай теоремы Паскаля. Пусть 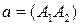 , где
, где 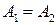 ,
, 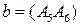 , где
, где 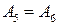 – заданные касательные.
– заданные касательные.
2) Построим касательную в третьей точке, т.е. прямую 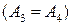 , где
, где 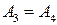 . Строим
. Строим 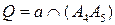 ,
, 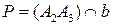 ,
, 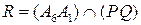 . Прямая
. Прямая 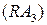 – искомая касательная.
– искомая касательная.

Рис. 60
2) Построим точку 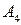 . Пусть
. Пусть 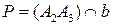 . Проводим через
. Проводим через 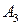 произвольную прямую
произвольную прямую 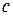 , не проходящую через
, не проходящую через 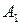 и
и 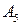 , и пусть
, и пусть  . Строим
. Строим 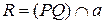 и
и 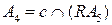 .
.

Рис. 61
Задача 22. Овальная кривая второго порядка задана тремя касательными к ней и точками касания двух из них. Построить:
1) еще одну касательную;
1) еще одну точку кривой.
Решение. Пусть  ,
,  ,
, 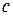 – заданные касательные и
– заданные касательные и 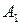 ,
, 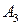 – точки касания,
– точки касания, 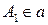 ,
, 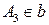 . Используем предельный случай теоремы Брианшона.
. Используем предельный случай теоремы Брианшона.
1) Пусть 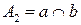 ,
, 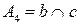 . Возьмем на касательной
. Возьмем на касательной 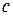 некоторую точку
некоторую точку 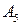 . Строим точку Брианшона
. Строим точку Брианшона 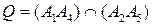 и
и 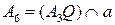 .
. 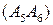 – искомая касательная.
– искомая касательная.
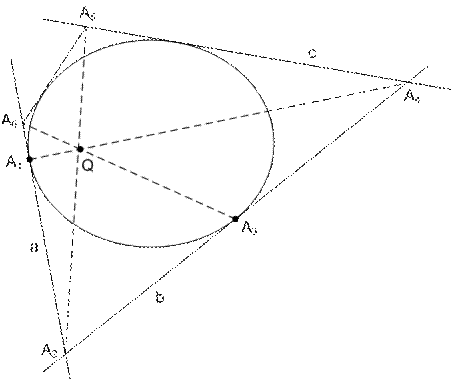
Рис. 62
2) Построим точку касания 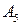 . Пусть
. Пусть 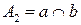 ,
, 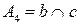 ,
, 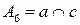 . Строим точку Брианшона
. Строим точку Брианшона 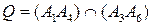 .
. 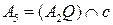 – искомая точка кривой.
– искомая точка кривой.
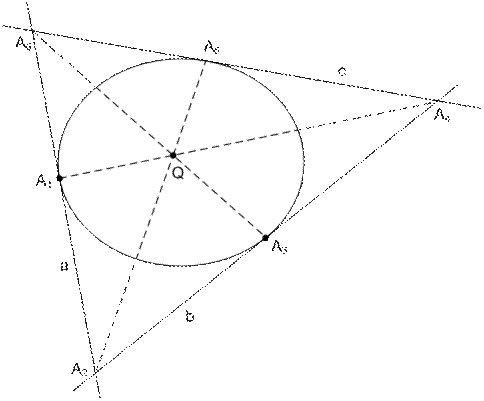
Рис. 63
Задача 23. На евклидовой плоскости даны ось, вершина и еще одна точка параболы. Построить касательную к параболе в этой точке.
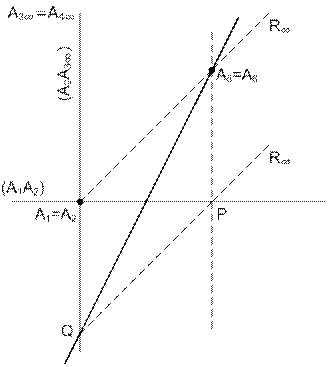
Рис. 64
Решение. Используем предельный случай теоремы Паскаля. Касательной к параболе в ее вершине является перпендикуляр к оси, поэтому вершину будем считать двойной точкой 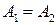 , а касательную обозначим как
, а касательную обозначим как 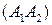 . Касательной к параболе в несобственной точке оси является несобственная прямая, поэтому обозначим несобственную точку оси как
. Касательной к параболе в несобственной точке оси является несобственная прямая, поэтому обозначим несобственную точку оси как 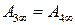 . Так как нас интересует касательная в заданной точке, то она также будет двойной точкой
. Так как нас интересует касательная в заданной точке, то она также будет двойной точкой 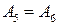 . Строим
. Строим 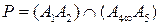 и
и 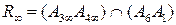 . Находим точку
. Находим точку  используя то, что
используя то, что 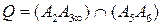 и
и 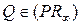 . Прямая
. Прямая 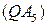 – искомая касательная в точке
– искомая касательная в точке 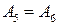 .
.
Задача 24. Даны две асимптоты гиперболы и одна ее точка. Построить:
1) касательную к гиперболе в данной точке;
2) еще одну точку гиперболы.
Решение. Известно, что асимптоты гиперболы на расширенной плоскости являются касательными в ее несобственных точках. Воспользуемся предельным случаем теоремы Паскаля. Несобственные точки асимптот будем считать двойными точками 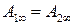 и
и 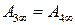 соответственно.
соответственно.
1) Заданную точку, в которой нужно провести касательную к гиперболе также будем считать двойной 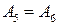 . Строим
. Строим 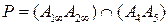 и
и 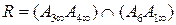 . Точка
. Точка  лежит на несобственной прямой
лежит на несобственной прямой 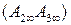 , т.е. является несобственной точкой прямой
, т.е. является несобственной точкой прямой 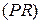 . Прямая
. Прямая  – искомая касательная.
– искомая касательная.
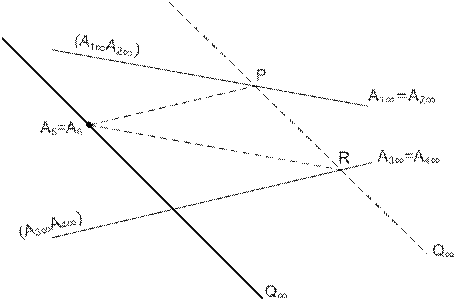
Рис. 64
1) Строим 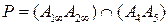 . Проводим через
. Проводим через 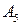 произвольную прямую
произвольную прямую  . Тогда
. Тогда  будет несобственной этой прямой, т.е.
будет несобственной этой прямой, т.е. 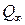 , так как
, так как  лежит на несобственной прямой
лежит на несобственной прямой 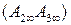 . Точку
. Точку 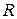 паскалевой прямой получаем из того, что
паскалевой прямой получаем из того, что 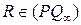 и
и 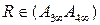 . Искомую
. Искомую 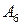 получаем как пересечение
получаем как пересечение 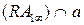 .
.

Рис. 65
| |
Сравнительное изучение теории инвариантов для аффинных, проективных и метрических пространств всегда составляло основу классического математического образования студентов педагогических вузов. Методы проективной геометрии являются эффективным инструментом для решения задач элементарной геометрии. Поэтому освещение различных вопросов элементарной геометрии с проективной точки зрения имеет прямое отношение к будущей работе учителей математики.
Курс проективной геометрии изучается после курса аналитической геометрии. Студенты уже знакомы с аффинными преобразованиями и движениями плоскости и трехмерного пространства и их инвариантами. Курс начинается строгим аксиоматическим изложением аффинной и евклидовой геометрии (по Вейлю). Затем при изучении центрального проектирования обосновывается необходимость конструирования проективного пространства и изучения инвариантов проективных преобразований.
В итоге студенты получают представление об инвариантах различных групп геометрических преобразований.
В настоящем пособии помещены задачи с подробными указаниями к их решению, что очень важно при самостоятельной работе над курсом, а также контрольные вопросы и задачи для самостоятельного решения. Ценность пособия возрастает при значительном сокращении часов, отводимых для изучения геометрии.
Приложение 2
Содержание курса Проективная геометрия
Дата добавления: 2016-03-27; просмотров: 5719;
