ГЛАВА 3. ЛИНИИ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
§17. Понятие проективной линии второго порядка
Множество всех точек проективной плоскости, координаты которых в некотором репере удовлетворяют действительному однородному уравнению второй степени, т.е. уравнению вида
a11(x1)2 + a22(x2)2 + a33(x3)2 + 2 a12x1 x2 + 2 a13x1 x3 + 2 a23x2 x3 = 0 (1)
называется линией или кривой второго порядка.
В однородном уравнении второй степени все действительные числа aij не обращаются одновременно в нуль. Положим для удобства aij = aji i,j = 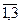 , тогда уравнение линии второго порядка можно записать в виде:
, тогда уравнение линии второго порядка можно записать в виде:
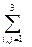 aij xi xj = 0
aij xi xj = 0
Если очевидны пределы суммирования, то, следуя правилу А.Эйнштейна, знак суммы можно опустить:
aij xi xj = 0 (2)
Понятие линии второго порядка является геометрическим и не зависит от выбора репера на проективной плоскости. Если фигура в репере Â = (A1, A2, A3, E) имеет уравнение (2), а Â' = (A'1, A'2, A'3, E') – другой проективный репер, формулы преобразования координат точек при переходе от репера Â к реперу Â' представляются в следующем виде (см. §7,(3)):
λ xj = bji yi , j = 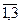 , λ ≠ 0 (3)
, λ ≠ 0 (3)
где (x1, x2, x3) – координаты точки в репере Â, а (y1, y2, y3) – координаты этой же точки в репере Â'. Подставляя выражения (3) в уравнение (2), имеем 0 = aij xi xj = aij ( 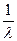 bik yk) (
bik yk) ( 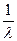 bjm ym) =
bjm ym) = 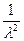 ( aij bik bjm) yk ym.
( aij bik bjm) yk ym.
Полагая a'ij = ars bri bsj, получаем уравнение линии второго порядка в репере Â':
a'ij yi yj = 0 (4)
Замечание. Индексы, по которым идет суммирование, называются "слепыми", их можно переобозначать, например: bjk yk = bjp yp.
Заметим, что det(bjk)3i,k=1 ≠ 0. В курсе линейной алгебры доказывается, что при умножении матрицы A на невыраженную матрицу B ранг матрицы A не меняется.
rg(A) =rg(A·B).
Значит, rg(aij)3i,j=1 = rg(a'ij)3i,j=1. Таким образом, в уравнении (4) не все коэффициенты при неизвестных равны нулю. Тем самым доказано, что, во-первых, понятие линии второго порядка не зависит от выбора репера, и, во-вторых, ранг матрицы, составленной из коэффициентов уравнения линии второго порядка, также не зависит от выбора репера. Таким образом, можно определить понятие ранга линии второго порядка, как ранг матрицы коэффициентов ее уравнения в некотором, а значит и в любом репере.
Линия второго порядка называется невырожденной, если ее ранг максимален, т.е. равен 3 (в этом случае det(aij) 3i,j=1 ≠ 0). И вырожденной, если rg(aij ) 3i,j=1 < 3. (Заметим, что для любой линии второго порядка ее ранг не равен нулю).
Лемма. Любая проективная прямая имеет с невыражденной проективной линией второго порядка не более двух различных общих действительных точек.
§18. Проективная классификация линий второго порядка.
Допустим, что линия второго порядка на проективной плоскости в некотором репере имеет общее уравнение
aij xi xj = 0 (1)
В трехмерном векторном пространстве V3 рассмотрим квадратичную форму q, т.е. для x(x1 x2 x3) 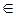 V3
V3
q( 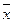 ) = aij xi xj (2)
) = aij xi xj (2)
Из курса линейной алгебры известно, что в трехмерном векторном пространстве V3 найдется базис, в котором квадратичная форма q имеет нормальный вид. Поскольку, согласно определению Г. Вейля, V3 порождает проективную плоскость P2, то в P2 найдется репер, в котором уравнение линии второго порядка имеет вид
ε1(x1)'(x1)' + ε2(x2)'(x2)' + ε3(x3)'(x3)' = 0 , (3)
где коэффициенты ε1, ε2, ε3 равны -1, 1 или 0, но одновременно все три коэффициента не обращаются в нуль.
Таким образом, мы приходим к каноническому уравнению линии второго порядка.
Перебирая все возможные варианты для коэффициентов ε1, ε2, ε3, убеждаемся, что на проективной плоскости существует пять типов линий второго порядка. Все они представлены в следующей таблице.
| № п.п. | Название линии | Каноническое уравнение | Ранг линии |
| Овальная линия | (x1)2+(x2)2-(x3)2=0 | ||
| Нулевая линия | (x1)2+(x2)2+(x3)2=0 | ||
| Пара прямых | (x1)2-(x2)2=0 | ||
| Пара мнимых прямых | (x1)2+(x2)2=0 | ||
| Пара совпадающих прямых | (x1)2=0 |
Указанные типы линий проективно различны, то есть не существует проективного преобразования, которое линию одного типа переводит в линию другого типа.
Однако, любые две линии одного и того же типа проективно эквивалентны.
Основное внимание в дальнейшем изложении мы будем уделять овальной линии.
Задача 43. Определить тип линии второго порядка
(x1)2 + 2x1x2 + 2(x2)2 - (x3)2 = 0.
§19. Пересечение проективной линии второго порядка с прямой. Касательная к линии второго порядка.
Допустим, что задана невыраженная (т.е. максимального ранга) линия второго порядка, имеющая в некотором репере уравнение
aij xi xj = 0 (1)
Кроме того, прямая d, проходящая через точки P (p1, p2, p3) и Q (q1, q2, q3), имеет в этом же репере параметрические уравнения
x1= λ p1 + μ q1; x2= λ p2 + μ q2; x3= λ p3 + μ q3 (2)
Поставим задачу нахождения точек пересечения линии второго порядка с прямой d. Для решения этой задачи подставим x1, x2 и x3 из параметрических уравнений прямой d в общее уравнение линии второго порядка. Ясно, что мы получим однородное уравнение второй степени относительно λ и μ:
A11 λ2 + 2A12λμ + A22μ = 0 (3)
Можно посчитать коэффициенты A11 A12 A22, из которых хотя бы один отличен от нуля:
A11 = aij pipj ; A12 = aij piqj ; A22 = aij qiqj ; (4)
Каждой ненулевой паре (λ, μ) действительных решений этого уравнения соответствует общая точка прямой и линии второго порядка. Однородное уравнение всегда имеет тривиальное решение, однако оно нам не подходит, так как, если λ = μ = 0, то x1 = x2 = x3 = 0, но на проективной плоскости нет точки, все координаты которой равны нулю. Допустим, что μ ≠ 0, тогда легко получить квадратное уравнение:
A11 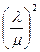 + 2A12
+ 2A12 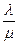 + A22 = 0 (5)
+ A22 = 0 (5)
Исследуем дискриминант этого уравнения
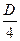 = (A12)2 – A11 A22 (6)
= (A12)2 – A11 A22 (6)
Если D > 0, то уравнение (5) и, соответственно, (3) имеет (с точностью до числового множителя) два непропорциональных вещественных решения относительно λ и μ. В этом случае прямая d пересекается с линией второго порядка в двух точках.
Если D < 0, то уравнение (3) не имеет вещественных решений, и линия второго порядкаи d не имеют вещественных общих точек.
Если D = 0, то линия второго порядкаи d имеют одну общую точку (две совпадающих точки). В этом случае прямая d называется касательной к линии второго порядка. Из соотношения (6) имеем условия касания:
(A12)2 - A11 A22 = 0 (7)
В каждой точке невыраженной линии второго порядка существует единственная касательная.
Если точка P (p1, p2, p3) принадлежит линии второго порядка, то A11 = aij pipj = 0, и условие касания (7) принимает простой вид:
A12 = 0 (8)
Расписывая соотношение (8), заменяя точку Q на текущую точку X(x1,x2,x3), приходим к уравнению касательной:
(a11p1+ a21 p2+ a31 p3) x1 +
(a12p1+ a22 p2+ a32 p3) x2 + (9)
(a13p1+ a23 p2+ a33 p3) x3 = 0
Напомним, что мы полагаем aij = aji для любых индексов i, j от 1 до 3.
Задача 44. Овальная линия в каноническом репере задана уравнением
(x1)2 + (x2)2 - (x3)2 = 0
Написать уравнение касательной прямой, проходящей через точку P(1,1, 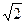 ).
).
§20. Полюс, поляра, поляритет.
Пусть на проективной плоскости P2 задана овальная линия γ, имеющая в некотором репере уравнение
aij xi xj = 0 (1)
Определение. Точки P (p1, p2, p3) и Q (q1, q2, q3) называются сопряженными относительно овальной линии, если выполняется условие
aij piqj = 0 (2)
На первый взгляд может показаться, что сопряженность двух точек относительно овальной линии зависит от выбора репера, поскольку уравнение овальной линии рассматривается в определенном репере. Однако, как мы убедимся позже, сопряженность точек относительно овальной линии носит геометрический характер, то есть не зависит от выбора репера на проективной плоскости.
Если точка P лежит на овальной линии, то, вспоминая уравнение касательной прямой к линии второго порядка ((9) §19), убеждаемся, что точки P и Q сопряжены относительно γ тогда и только тогда, когда точка Q лежит на касательной к линии второго порядка в точке P.
Следующая теорема раскрывает геометрический смысл сопряженности двух точек, не лежащих на данной овальной линии.
 |
Теорема. Пусть на проективной плоскости заданы овальная линия γ, и две точки P и Q, не лежащие на γ, причем прямая (PQ) пересекает γ в двух различных точках M и N. Для того, чтобы P и Q были сопряжены относительно γ, необходимо и достаточно, чтобы пара точек P и Q гармонически разделяла пару точек M и N, (т.е. чтобы сложное отношение четырех точек P, Q, M и N было равно -1: (PQ, MN) = -1.
Рис. 17.
Доказательство. Выберем на проективной плоскости произвольный репер R = (A1, A2, A3, E), пусть в этом репере овальная линия имеет уравнение (1) и точки P и Q приобретают проективные координаты P (p1, p2, p3) , Q (q1, q2, q3); прямая (PQ) задается параметрическими уравнениями
x1= λ p1 + μ q1; x2= λ p2 + μ q2; x3= λ p3 + μ q3 (3)
Пусть точки пересечения прямой (PQ) и овальной линии имеют следующие координаты:
M(λ1 p1 + μ1 q1, λ1 p2 + μ1 q2, λ1 p3 + μ1 q3)
N(λ2 p1 + μ2 q1, λ2 p2 + μ2 q2, λ2 p3 + μ2 q3) .
Вычислим сложное отношение (PQ, MN). Обозначим через P′, Q′, M′, N′ проекции точек P, Q, M, N на координатную прямую (A1A2) из центра A3, тогда в репере R3 = (A1, A2, E3) (E3 =( A3 E ∩ (A1 A2)) имеем P′ (p1, p2) ,
Q′ (q1, q2), M′(λ1 p1 + μ1 q1, λ1 p2 + μ1 q2), N′(λ2 p1 + μ2 q1, λ2 p2 + μ2 q2).
(PQ, MN) = (P′Q′, M′N′) = 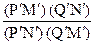 =
=
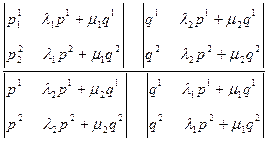 =
= 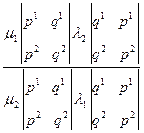 =
= 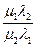
Заметим, что 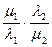 = -1 тогда, и только тогда, когда
= -1 тогда, и только тогда, когда  = 0
= 0
Подставляя соотношение (3) в уравнение (1), получаем после деления на λ2:
A22 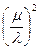 + 2A12
+ 2A12 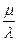 + A11 = 0 (4)
+ A11 = 0 (4)
Поскольку точки P и Q не лежат на овальной линии, то A22 = aijpiqj ≠ 0 A11 = aij piqj ≠ 0.
Так как точки M и N лежат на овальной линии, то  = -
= - 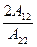 .
.
Точки P и Q сопряжены относительно γ тогда и только тогда, когда aijpiqj = A12= 0, т.е. P и Q сопряжены, если и только если  = 0, что в свою очередь равносильно тому, что (PQ, MN) = -1.
= 0, что в свою очередь равносильно тому, что (PQ, MN) = -1.
Определение. Пусть на проективной плоскости задана овальная линия γ и точка P. Полярой называется множество точек d, сопряженных с точкой P относительно γ, а сама точка P называется полюсом поляры d.
Если овальная линия задается в некотором репере уравнением (1), точка P имеет координаты (p1, p2, p3), то из условия сопряженности (2) получаем уравнение поляры d:
(ai1pi) x1 + (ai2pi) x2 + (ai3pi) x3 = 0 (5)
Поскольку овальная линия невырождена, то не все коэффициенты при x1, x2, x3 равны нулю, поэтому d – прямая. Для каждой точки P (p1, p2, p3), проективной плоскости существует поляра (5) относительно овальной линии (1), и обратно для каждой прямой u1 x1 + u2x2 + u3x3 = 0 существует единственный полюс P, координаты которого определяются системой уравнений
a11p1+ a21 p2+ a31 p3 = λu1
a12p1+ a22 p2+ a32 p3) = λu2
a13p1+ a23 p2+ a33 p3) = λu3,
где λ ≠ 0.
Овальная линия не вырождена, определитель системы не равен нулю, поэтому точка P определяется однозначно (координаты точки P находятся с точностью до ненулевого множителя).
Таким образом, любая овальная линия определяет биекцию P2 → (P2)′ проективной плоскости P2 на множество (P2)′ ее прямых.
Теорема о взаимности поляритета. Пусть на проективной плоскости задана овальная линия. Если точка Q лежит на поляре точки P, то точка P лежит на поляре точки Q.
Задача 45. С помощью одной линейки (без циркуля) построить касательную, проходящую через заданную точку, к заданной овальной линии на расширенной плоскости.
Задача 46.Пусть на расширенной плоскости задана овальная линия. По данному полюсу построить поляру; по данной поляре построить полюс.
§21. Теорема Штейнера.
Теорема Штейнера позволяет дать геометрическое определение овальной линии второго порядка при помощи отображения одного пучка прямых на другой.
Теорема Штейнера. На проективной плоскости множество точек пересечения соответствующих прямых двух проективных, но не перспективных пучков есть невырожденная кривая второго порядка. И обратно, два пучка с центрами на кривой второго порядка, у которых соответствующие прямые пересекаются на этой кривой – проективны.
Доказательство. Пусть даны два пучка с различными центрами O1 и O2 и установлено проективное, но не перспективное отображение f первого пучка на второй. Докажем, что множество γ точек пересечения соответственных прямых этих пучков есть овальная линия, проходящая через точки O1 и O2.
 |
Обозначим через m прямую (O1O2) и рассмотрим прообраз n этой прямой m=f(n). Отображение f зададим с помощью трех попарно различных прямых n, m, l пучка O1 и их образов m, m′, l′ в пучке O2:
f: n 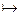 m; m
m; m 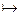 m′; l
m′; l 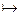 l′
l′
Прямые n, m′, l′ попарно различны, так как f не является перспективным отображением, поэтому точки O1=n∩m, O2=m∩m′ и O3=n∩m′ не лежат на одной прямой, точка E=l∩ l′ не принадлежит прямым m, m′, n, следовательно, мы получим репер Â = (O1, O2 , O3 ,E,).
Пусть X (x1, x2, x3) произвольная точка, не лежащая на сторонах трехвершинника O1O2O3 . По определению сложного отношения прямых (mn, l(O1 X)) = (O2O3,E1,X1), и (m′m, l′(O2 X)) = (O3O1,E2,X2) (см. рисунок 18).
В репере R2 = (O2, O3 ,E1) на координатной прямой (O1O2) точка X1 имеет координаты (x2, x3), поэтому (O2O3,E1,X1) = 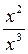 . Аналогично, (O3O1,E2,X2) =
. Аналогично, (O3O1,E2,X2) = 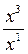 . Таким образом, (mn, l(O1X)) =
. Таким образом, (mn, l(O1X)) = 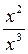 ; (m′m, l′(O2X)) =
; (m′m, l′(O2X)) = 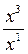 .
.
Если X 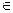 γ, то в силу сохранения проективным отображением сложного отношения имеем (mn, l (O1 X)) = (m′m, l′ (O2X)).
γ, то в силу сохранения проективным отображением сложного отношения имеем (mn, l (O1 X)) = (m′m, l′ (O2X)).
Поэтому 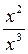 =
= 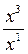 , и мы получаем уравнение линии второго порядка:
, и мы получаем уравнение линии второго порядка:
(x1x2) - (x3)2 = 0 (1)
Если Х 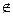 γ, то (mn, l (O1X)) ≠ (m′m, l′ (O2X)), и
γ, то (mn, l (O1X)) ≠ (m′m, l′ (O2X)), и 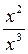 ≠
≠ 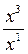 , т.е. координаты точки Х не удовлетворяют уравнению (1). Если точка X лежит на сторонах трехвершинника O1O2O3, то ее координаты удовлетворяют уравнению (1), если, и только если Х совпадает с одной из точек O1(1,0,0) и O2(0,1,0), которые принадлежат множеству γ. Уравнение (1) есть уравнение второй степени, ранг максимален, следовательно, оно определяет невыраженную линию второго порядка, на которой есть действительные точки O1 и O2, т.е. овальную линию.
, т.е. координаты точки Х не удовлетворяют уравнению (1). Если точка X лежит на сторонах трехвершинника O1O2O3, то ее координаты удовлетворяют уравнению (1), если, и только если Х совпадает с одной из точек O1(1,0,0) и O2(0,1,0), которые принадлежат множеству γ. Уравнение (1) есть уравнение второй степени, ранг максимален, следовательно, оно определяет невыраженную линию второго порядка, на которой есть действительные точки O1 и O2, т.е. овальную линию.
Обращая рассуждения, получаем вторую часть теоремы Штейнера.
Задача 47. Сформулировать предложение, двойственное теореме Штейнера.
§22. Теоремы Паскаля и Брианшона .
Пусть шесть точек A1, A2,…, A6 заданы на овальной линии второго порядка. Тогда три точки пересечения прямых (A1, A5) и (A2, A4), (A3, A4) и (A1, A6), (A2, A6) и (A3, A5) лежат на одной прямой.
Если шестивершинник есть любая шестизвенная замкнутая ломанная, а под сторонами шестивершинника понимают прямые, содержащие звенья ломанной, то теорему Паскаля можно сформулировать следующим образом.
Теорема Паскаля. Противолежащие стороны шестивершинника, вписанного в овальную линию второго порядка, пересекаются в точках, лежащих на одной прямой.
Рисунок 19.
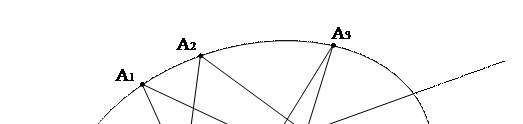 |
Доказательство. Пусть вершины шестивершинника A1 A2 A3 A4 A5 A6 лежат на овальной линии γ. Докажем, что точки O = (A1A6) ∩ (A3A4), N = (A2A4) ∩ (A1A5) и N′ = (A2A6) ∩ (A3A5) лежат на одной прямой (см. рисунок 20).

Рисунок 20.
Пусть f – проективное отображение пучков с центрами A1 и A3, которое устанавливается овальной линией γ согласно теореме Штейнера. Отображение f порождает проективное отображение φ: (A2, A4)→(A2, A6), в которой каждой точке Х1 на (A2, A4) соответствует точка Х2 прямой (A2,A6), такая, что прямые (A1, Х1) и (A3,Х2) пересекаются в точке Х, принадлежащей линии γ. Поскольку φ(A2)= A2, то φ – перспективное отображение, центром его является точка O, причем N′ = φ(N), следовательно N, O, N′ принадлежат одной прямой.
Обратная теорема Паскаля. Если точки пересечения противоположных сторон шестивершинника лежат на одной прямой, то все его вершины лежат на овальной линии второго порядка.
Замечание. Если в теореме Паскаля овальную линию заменить на пару прямых, то мы приходим к теореме Папа.
Двойственной к теореме Паскаля является следующая
Теорема Брианшона. Шестивершинник описан около овальной линии второго порядка тогда и только тогда, когда его большие диагонали пересекаются в одной точке.

Задача 48. Даны пять точек общего положения и прямая, проходящая через одну из них и не проходящая через остальные точки. Построить вторую точку пересечения данной прямой с овальной линией, проходящей через данные пять точек.
Дата добавления: 2016-03-27; просмотров: 2891;
