Состояние фаз в молоке
| Компоненты | Жировая фаза | Белковая фаза | |
| жировые шарики, липопротеиновые оболочки | гидратированные мицеллы казеина, соли | сывороточные белки | |
| Состояние системы | Грубая дисперсия | Тонкая дисперсия | Коллоидный раствор |
| Содержание, % | 3,8 | 3,2 | 0,8 |
| Объемная доля | 0,042 | 0,065 | 0,006 |
| Диаметр частицы | 0,1-1 мкм | 10-300 нм | 3-6 |
| Число частиц в 1 мл | 1010 | 1014 | 1017 |
| Размер поверхности, см2/мл | |||
| Плотность при 200С, г/мл | 0,92 | 1,11 | 1,34 |
| Способ выделения | Сепарирование | Ультрацентрифугирование | Гельфильтра-ция |
Дисперсные структуры условно можно также подразделить на два основных типа, различающихся по видам взаимодействия частиц дисперсной фазы. Первая группа, включающая коагуляционные структуры, характеризуется тем, что пространственный каркас обладает небольшой прочностью, так как взаимодействие частиц происходит за счет молекулярных сил через прослойки жидкости. Отличительной особенностью коагуляционных структур является тиксотропия - явление полного восстановления структуры после предельно возможного ее разрушения под воздействием механической нагрузки (сдвигающей деформации).
Образование конденсационно-кристализационных структур происходит за счет непосредственного взаимодействия частиц и их срастания с образованием жесткой объемной структуры. Подобные структуры типичны для связанодисперсных систем. Для них характерны фиксированная структура и геометрические размеры, прочность, хрупкость и неспособность к обратимому восстановлению после механического разрушения. Если частицы аморфные, то структуры, образующиеся в дисперсных системах, принято называть конденсационными; если частицы частично кристаллические, то структуры являются кристаллизационными.
Под структурой тел обычно понимают пространственное взаимное расположение составных частей тела. Структуру, т.е. внутреннее строение продукта и характер взаимодействия между отдельными элементами, определяют химический состав, дисперсность, биохимические и технологические факторы.
По природе устойчивости и интенсивности межмолекулярных взаимодействий на границе раздела фаз дисперсные системы подразделяются на лиофильные и лиофобные. Для лиофильных дисперсных систем характерна высокая степень родственности дисперсной фазы и дисперсионной среды и малая интенсивность поверхностных сил на границе раздела фаз, чему отвечают очень низкие значения поверхностной энергии на межфазных поверхностях. Эти коллоидные системы могут образовываться самопроизвольно из соответствующих макроскопических фаз; для них характерно термодинамически равновесное распределение частиц дисперсной фазы по размерам (а иногда и по форме), которое зависит только от состава и условий существования системы. В лиофобных дисперсных системах (коллоидно- и грубодисперсных) дисперсная фаза и дисперсионная среда менее родственны, и различие граничащих фаз по химическому составу и строению проявляется в слабом межфазном взаимодействии, большой интенсивности поверхностных сил и значительном избытке энергии на межфазной поверхности. Такие системы термодинамически неустойчивы и требуют специальной стабилизации.
Наличие развитой поверхности и связанной с ней большой поверхностной энергии обусловливает необходимость затраты значительной работы на образование лиофобных дисперсных систем как путем измельчения (диспергирования) макроскопических фаз, так и при выделении (конденсации) новых дисперсных фаз из гомогенных систем. Избыточная поверхностная энергия обусловливает повышение химической активности вещества дисперсной фазы в высокодисперсном состоянии тем больше, чем меньше размер частиц дисперсной фазы. Это проявляется в увеличении растворимости вещества дисперсной фазы в окружающей среде и повышении давления пара над малыми частицами. Повышенная химическая активность и развитая поверхность раздела фаз определяют высокую скорость процессов взаимодействия между дисперсной фазой и дисперсионной средой - переноса массы и энергии между ними в гетерогенных химических процессах.
Наличие избытка поверхностной энергии, особенно в высокодисперсных системах, обусловливает главную особенность лиофобных дисперсных систем - их термодинамическую нестабильность и возможность протекания в них процессов, ведущих к понижению поверхностной энергии за счет уменьшения площади поверхности раздела фаз или насыщения поверхностных сил. Это ведет к изменению строения дисперсных систем и их разрушению.
Современная пищевая технология рассматривает широкий диапазон дисперсных систем: от грубодисперсных с частицами от 1 мкм и выше и удельной поверхностью S1<1 м2/г до высокодисперсных, в т.ч. ультрамикрогетерогенных коллоидных наносистем с частицами до 1 нм и удельными поверхностями, достигающими 1000 м2/г. Грубодисперсные системы содержат частицы, оседающие в гравитационном поле и не проходящие через бумажные фильтры, видимые в обычный световой микроскоп. Частицы высокодисперсных систем невидимы в световой микроскоп, практически не оседают и не проходят через бумажные фильтры. Частицы высокодисперсных систем могут быть обнаружены с помощью электронного или ультрамикроскопа; они задерживаются ультрафильтрами и могут быть отделены с помощью центробежного поля.
Высокодисперсные системы можно разделить на ультрамикрогетерогенные с размером частиц от 10-7 до 10-5 см и микрогетерогенные с размерами частиц от 10-5 до 10-3 см. Частицы с меньшими размерами, чем 10-7 см, образуют молекулярные или ионные растворы. К грубодисперсным системам относят вещества с размером частиц, превышающим 10-3 см. Для связанодисперсных систем классификация по дисперсности основывается на размерах пор веществ. Пористые тела с размером пор до 2×10-5 см следует отнести к микропористым системам, от 2×10-7 до 2×10-5 см - к переходнопористым, превышающим 2×10-5 см - к макропористым.
Высокодисперсное состояние вещества служит условием высокой организации материи. Тонкодисперсная структура обусловливает необходимые структурно-механические характеристики. Лишь на высокоразвитых межфазных поверхностях, т.е. в высокодисперсных системах, интенсивно протекают гетерогенные химические реакции. Только высокодисперсная структура, т.е. множество мельчайших субъединиц материи, позволяет хранить и использовать огромные объемы информации в малых физических объемах.
Основные закономерности адсорбционных явлений на границах раздела фаз при введении в систему третьего компонента (ПАВ) подчиняется правилу уравнивания П.А. Ребиндера, в соответствии с которым поверхностно-активным является компонент, способный скомпенсировать скачек полярностей, существующий на границе раздела двух разнородных фаз, состоящих из взаимно ограниченно растворимых (или практически нерастворимых) веществ.
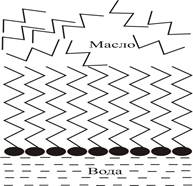
Рис. 2.1. Ориентация ПАВ на межфазной границе вода
Подобное уравнивание, или «сглаживание» разности полярностей в межфазной поверхности разрыва возможно в том случае, когда полярность третьего компонента оказывается промежуточной между полярностями двух других компонентов, образующих контактирующие фазы. Наиболее полное сглаживание полярностей происходит при адсорбции дифильных веществ, молекулы которых имеют резко различающиеся по полярности участки. Таковы органические ПАВ, способные компенсировать разность полярностей между водой и любой (жидкой или твердой) углеводородной фазой. Молекулы ПАВ при этом ориентируются полярной группой в воду, а углеводородной цепью - в сторону «масла», создавая переходный слой, который при достаточно высоких значениях адсорбции в большой мере или даже практически полностью сглаживает разность полярностей между двумя фазами.
Как ранее отмечалось, особенностью свойств дисперсных систем является то, что значительная доля всех молекул и атомов располагается на поверхности раздела фаз. Эта часть вещества по своему положению находится в несимметричном силовом поле, а также отличается по своему энергетическому состоянию. Действительно, создание межфазной поверхности требует затраты работы по разрыву связей, значительная часть которой накапливается в виде избыточной потенциальной энергии на межфазной границе.
Избыток свободной энергии делает дисперсии системами, стремящимися к уменьшению дисперсности. При этом система, оставаясь неизменной по химическому составу, изменяет энергетические характеристики и, следовательно, коллоидно-химические свойства.
Все эти особенности имеют решающее значение при создании продуктов с дисперсной структурой. Потенциальные возможности реализации этого направления в отечественной пищевой промышленности, основанные на знании свойств дисперсных систем, практически неограниченны, однако развиты недостаточно сильно.
Если форма частиц дисперсной фазы близка к изометрической, то степень раздробленности этой фазы может характеризоваться линейным размером частиц (средним радиусом r), дисперсностью Q либо удельной поверхностью S1. Дисперсность Q определяют как отношение суммарной поверхности раздела дисперсной фазы 1 с дисперсной средой 2 (межфазной поверхности) S12 к суммарному объему этих частиц V1:
Q= 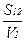 , (2.1)
, (2.1)
Удельная поверхность S1 - это отношение суммарной поверхности к общей массе частиц:
S1= 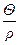 , (2.2)
, (2.2)
где r - плотность веществ дисперсной фазы.
Для монодисперсной системы, состоящей из сферических частиц радиусом r, имеем:
D= 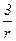 . (2.3)
. (2.3)
Наиболее полная информация, которая может быть получена при дисперсионном анализе, включает в себя функции распределения частиц по размерам, а в некоторых случаях и по форме частиц. Различают дифференциальные и интегральные (кумулятивные) функции распределения частиц по размерам, которые связаны между собой соответственно операциями дифференцирования и интегрирования, т.е. необходимо рассмотреть два параметра: что распределено, и почему (по какому признаку) рассматривается распределение. Первым параметром может быть число частиц, их суммарный объем, масса, суммарная поверхность. Второй параметр характеризует размер частиц: радиус, объем, массу, реже - поверхность. Соответственно, если рассматривается дифференциальная функция распределения, например, числа частиц по радиусам fn(r), то она имеет вид:
fn(r)= 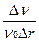 . (2.4)
. (2.4)
Величина fn(r) представляет собой число частиц Dn с радиусами в интервале от r+ 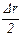 , отнесенное к общему числу частиц размеров n0 и величине Dr, т.е. долю общего числа частиц, приходящуюся на частицы в рассматриваемом интервале радиусов.
, отнесенное к общему числу частиц размеров n0 и величине Dr, т.е. долю общего числа частиц, приходящуюся на частицы в рассматриваемом интервале радиусов.
В зависимости от метода дисперсионного анализа могут получаться либо непрерывные функции распределения (Dr®0), либо гистограммы, в которых высота столбов отражает количество вещества в заданном интервале радиусов, а ширина - величины Dr (не всегда одинаковые в разных областях размеров частиц).
Интегральная функция распределения qn(r) связана с дифференциальной соотношением:
qn(r)= 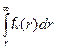 . (2.5)
. (2.5)
qn(r) представляет собой долю общего числа частиц, приходящуюся на частицы с радиусом большим r (именно так принято определять интегральные функции распределения в коллоидной химии, тогда как при изучении молекулярно-массового распределения растворов макромолекул обычно рассматривают суммирование по массам молекул).
Использование интегральных функций распределения обусловлено двумя обстоятельствами: во-первых, они имеют более простую форму, и поэтому для них легче осуществлять сглаживание полученной кривой, и, во-вторых, по ним проще определять долю частиц, приходящихся на определенный интервал размеров Dr (равна разности соответствующих значений q(r+Dr)-q(r)).
Разные методы дисперсионного анализа в качестве первичной информации дают различные функции распределения в зависимости от того, какие параметры измеряются в эксперименте; в дальнейшем часто производится пересчет к другим параметрам. При этом необходимо учитывать, что при таком пересчете могут возникать погрешности, величина которых может быть различной в разных интервалах размеров частиц.
В соответствии с различными функциями распределения по разному определяются и средние размеры частиц (rср). В общем случае справедливо равенство:
rср= 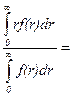
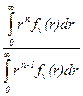 , (2.6),
, (2.6),
где показатель степени n определяется видом использованной функции распределения.
Для объективной характеристики дисперсности вещества необходимо в первую очередь знать форму поверхности и размер частиц. Если дисперсная среда является жидкой, то частицы в газообразной среде или газообразная фаза в жидкой среде имеют сферическую форму, которую обретают капли в момент образования в результате действия поверхностных сил, стремящихся свести поверхность частицы к наименьшей при данном объеме и обеспечивать термодинамическую устойчивость капельки. Например, в вакууме при отсутствии гравитационных сил жидкость приобретает идеальную сферическую форму поверхности. В этом случае все геометрические параметры частицы достаточно точно характеризуются ее диаметром, который и определяет размеры частицы.
В отличие от этого поверхность частицы твердого тела в общем случае характеризуется участками различной кривизны и имеет неправильную геометрическую форму, и размер частицы зависит от направления измерения и является переменной величиной. В качестве величины, определяющей размер такой частицы, используют приведенный или эквивалентный диаметр, под которым понимают диаметр условной сферической частицы, имеющей одинаковый объем с частицей сложной формы.
Для определения эквивалентного диаметра частиц произвольной формы в зависимости от метода измерения используют различные расчетные формулы. Если имеются данные по измерению частицы в трех взаимно-перпендикулярных направлениях, за эквивалентный диаметр Dэ принимают среднеарифметическое высоты h, ширины b и длины l:
Dэ1= 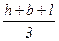 . (2.7)
. (2.7)
В связи со сложностью определения высоты частиц большинством применяемых методов и средств анализа нахождение эквивалентного диаметра упрощают и используют в расчетах только длину l и ширину b.
Dэ2= 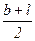 (2.8)
(2.8)
Более точные значения дают результаты определения эквивалентного диаметра, найденные как среднегеометрическое из произведения длины и ширины для частиц, проекция которых близка к кругу или квадрату.
Dэ3= 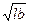 (2.9)
(2.9)
Для частицы в форме призмы аналогичный результат можно получить с помощью оценки по уравнению равновеликой поверхности частиц:
Dэ4= 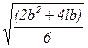 . (2.10)
. (2.10)
Эквивалентный диаметр можно определить и по равновеликому объему частицы:
Dэ5= 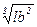 , (2.11)
, (2.11)
и по площади проекции частицы в поле зрения микроскопа Sп:
Dэ6= 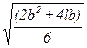 . (2.12)
. (2.12)
Диаметр, рассчитанный по этой формуле, называют также проектированным диаметром частицы. Объем частицы наиболее просто рассчитать для сферической частицы. Для расчета объема частиц, форма которых произвольна, используют объемный коэффициент формы аv, который связывает диаметр частицы и ее объем:
V= аv×( Dэ6)3. (2.13)
Установлено, что объемный коэффициент в зависимости от интервала размеров частиц сохраняет постоянное значение. В интервалах размеров от 1 до 60 мкм коэффициента аv изменяется от 0,524 до 0,14-0,20 для частиц шарообразной и неправильной форм. В тех случаях, когда частицы измеряют с помощью микроскопа в трех проекциях, рекомендуется пользоваться расчетными значениями объемного коэффициента, который можно найти из уравнения:
аv = 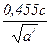 (2.14),
(2.14),
где с - отношение толщины частицы к ее проектированному диаметру;
a/ - отношение длины частицы к ее проектированному диаметру.
При известных значениях с и a/ расчетные значения объемного коэффициента можно найти, воспользовавшись табл. 2.4.
Таблица 2.4
Дата добавления: 2016-03-22; просмотров: 1662;
