Примеры контрольных карт для альтернативных данных

- и - Карты. Стандартные значения не заданы.

В таблице 13 указано число несоответствующих единиц в час с учетом неисправностей, найденных при сплошном контроле небольших выключателей с помощью устройств автоматического контроля. Выключатели производят на автоматической сборочной линии. Поскольку неисправность серьезна, для определения момента выхода сборочной линии из статистически управляемого состояния используют контрольную карту процента несоответствующих единиц. -Карта получена при сборе предварительных данных по 25 подгруппам каждая из 4000 выключателей (таблица 13).

Табл. 13.Выключатели. Предварительные данные

Номер подгруппы	Число проконтролированных выключателей	Число несоответствующих выключателей	Процент несоответствий	Номер подгруппы	Число проконтролированных выключателей	Число несоответствующих выключателей	Процент несоответствий
			0,200				0,200
			0,350				0,375
			0,250
			0,100				0,275
			0,325				0,225
							0,450
			0,225				0,150
			0,175				0,300
			0,275
			0,375 0,325				0,150 0,300 0,200
			0,126 0,350				0,375 0,350
			0,300	Всего			0,269

Центральная линия и контрольные границы вычислены ниже и приведены на рисунке 18.

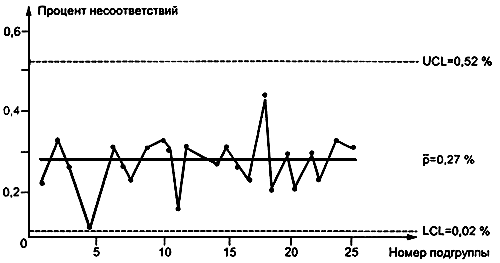
Рис. 18. -Карта по данным таблицы 13

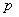-Карта:

центральная линия: ;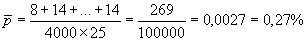

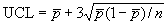= 0,0027 + 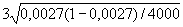= 0,52%;

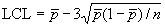= 0,0027 - 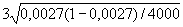= 0,02%.

Карта показывает, что качество выключателей находится в управляемом состоянии, хотя процент несоответствий, видимо, слишком велик. Данные контрольные границы могут быть использованы для будущих подгрупп до тех пор, пока процесс не изменится или выйдет из статистически управляемого состояния. Когда же процесс находится в состоянии статистической управляемости, вряд ли удастся какое-либо усовершенствование без изменения самого процесса.

Если сделано улучшение процесса, надо вычислить новые контрольные границы для будущих подгрупп, чтобы учесть измененное качество процесса. Если процесс улучшен (значение уменьшилось), то нужно использовать новые границы. Если процесс был ухудшен (значение р увеличилось), надо найти дополнительные неслучайные причины.

Отметим, что для приведенных данных в той же степени пригодна -карта, поскольку объемы всех выборок равны. Вычисления для -карты даны в таблице 13, карта представлена на рисунке 19.

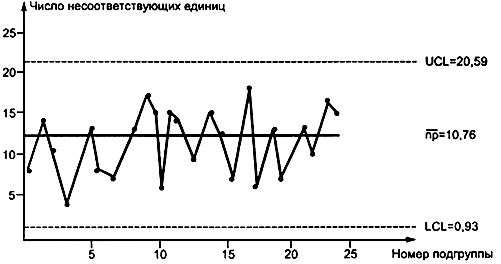
Рис. 19. -Карта по данным таблицы 13

-Карта:

центральная линия: ;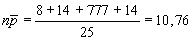

;

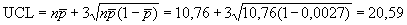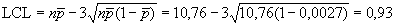-Карта. Стандартные значения не заданы.

В компании, изготавливающей транзисторы, было решено ввести карту доли несоответствующих единиц . Были собраны и проанализированы данные за 1 мес. Из продукции ежедневно в конце дня извлекались случайные выборки и регистрировалось количество несоответствующих единиц. Данные приведены в таблице 14.

Табл. 14.Транзисторы. -Карта

(первоначальные данные)

Номер подгруппы	Число проконтролированных единиц	Число несоответствующих единиц np	Доля несоответствующих единиц p	UCL	LCL	Номер подгруппы	Число проконтролированных единиц	Число несоответствующих единиц np	Доля несоответствующих единиц p	UCL	LCL
			0,070	0,117	0,003				0,055	0,119	0,001
			0,079	0,120	0,000				0,038	0,116	0,004
			0,057	0,120	0,000
			0,039	0,177	0,003				0,091	0,115	0,005
			0,025	0,116	0,004				0,132	0,121	0,000
									0,065	0,118	0,002
			0,049	0,119	0,001				0,060	0,118	0,002
			0,072	0,120	0,000				0,034	0,119	0,001
			0,073	0,118	0,002
			0,055	0,116	0,004				0,000	0,121	0,000
			0,038	0,119	0,001				0,073	0,115	0,005
									0,070	0,120	0,000
			0,013	0,118	0,002				0,058	0,121	0,000
			0,046	0,118	0,002				0,097	0,119	0,001
			0,047	0,118	0,002				0,124	0,116	0,004
						Всего

Средняя доля несоответствующих единиц за месяц подсчитывалась следующим образом:

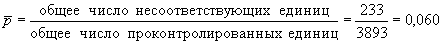Поскольку объемы подгрупп различны, значения UCL и LCL вычисляют для каждой подгруппы отдельно по формуле .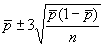

Значения UCL и LCL также приведены в таблице 14. Очевидно, что вычисление значений и построение линий UCL и LCL для каждой подгруппы достаточно трудоемко. Однако из таблицы 14 можно понять, что доли несоответствующих единиц для подгрупп № 11 и 26 не лежат в соответствующих пределах. Эти две подгруппы были исключены из данных, поскольку они подверглись другим неслучайным изменениям. Включение их в расчеты привело бы к завершению среднего и контрольных границ. Причины этих высоких значений должны быть найдены, чтобы предпринять соответствующие корректирующие действия для предотвращения их будущих появлений. Пересмотренная средняя доля несоответствующих единиц вычислена для значений остальных 24 подгрупп.

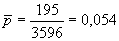Подсчет UCL и LCL для каждой подгруппы с использованием пересмотренного значения 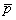выявляет, что все доли несоответствующих единиц находятся внутри соответствующих контрольных границ. Поэтому пересмотренное значение 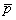взято в качестве стандартной доли несоответствующих единиц для построения контрольных карт. Таким образом, 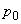= 0,054.

Как отмечалось выше, построение верхних контрольных границ для каждой подгруппы переменного объема - трудоемкий и кропотливый процесс. Однако поскольку объемы подгрупп не сильно отличаются от среднего объема выборки, равного 150, пересмотренная -карта (с использованием 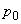= 0,054) может быть построена с использованием верхней контрольной границы для среднего объема подгруппы, равного 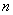= 150. Тогда можно вычислить линии пересмотренной -карта.

Пересмотренная -карта:

центральная линия 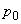= 0,054;

;

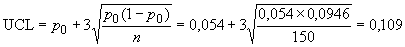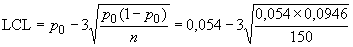(так как отрицательные значения невозможны, нижняя граница отсутствует).

Карта на рисунке 20 показывает состояние статистической управляемости процесса.

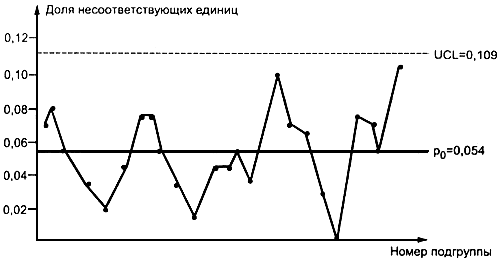
Рис. 20. Пересмотренная -Карта по данным таблицы 14

-Карта. Стандартные значения не заданы.

Производитель видеокассет желает управлять числом точечных несоответствий на видеоленте. Видеолента производится длиной 4000 м. Представленные данные показывают число точечных несоответствий, найденных последовательным обследованием поверхности 20 мотков видеоленты, каждый длиной 350 м, из одного производственного процесса, причем обследовался один конец ленты. Чтобы управлять этим процессом, намечено применить -карту, нанося число точечных несоответствий. Данные для 20 мотков приведены в таблице 15 и взяты в качестве предварительных данных для подготовки -карты.

Табл. 15. Видеолента. Предварительные данные

Номер мотка

Всего

Число точечных несоответствий

Центральная линия и контрольные границы вычислены ниже и приведены на рисунке 21.

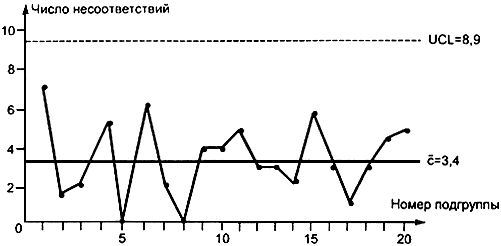
Рис. 21. -Карта по данным таблицы 15

-Карта:

центральная линия: ;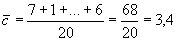

;

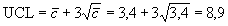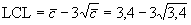(т.к. отрицательные значения невозможны, нижняя граница отсутствует).

Предварительные данные показывают, что процесс находится в состоянии статистической управляемости.

-Карта. Число несоответствий на единицу.

На заводе по производству шин каждые полчаса контролировали 15 шин и записывали общее число несоответствий и их число на единицу. Было решено применить -карту для числа несоответствий на единицу, чтобы определить состояние процесса. Данные приведены в таблице 16.

Табл. 16. Завод по производству шин.

Число несоответствий на единицу (единицы проверялись

по 14 подгруппам, объемом 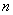= 15 каждая)

Номер подгруппы	Число несоответствий c	Число несоответствий на единицу u	Номер подгруппы	Число несоответствий c	Число несоответствий на единицу u
		0,27			0,13
		0,33			0,27
		0,20			0,47
		0,40			0,33
		0,13			0,13
		0,07			0,20
		0,33	Всего
		0,40

Среднее значений подсчитывалось из таблицы 16 делением общего числа несоответствий (из ряда 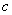-значений) на общее число проконтролированных единиц (т.е. 14 х 15).

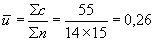-Карта:

центральная линия: = 0,26;

;

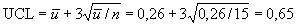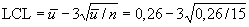(т.к. отрицательные значения невозможны, нижняя граница отсутствует).

Данные и контрольные линии нанесены на рисунке 22. Карта показывает, что процесс находится в состоянии статистической управляемости.

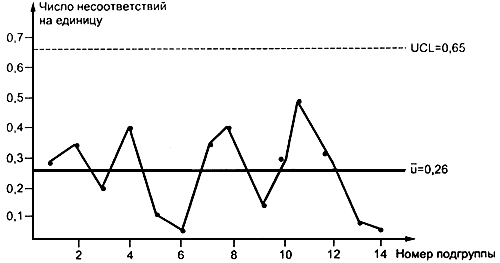
Рис. 22. -Карта по данным таблицы 16

Отметим, что поскольку объемы подгрупп постоянны, можно применить и -карту.

2.5. Задачи для самостоятельной работы

Задача № 1. При анализе технологического процесса в течении 25 часов каждый час отбиралось по пять проб, которые анализировались в химической лаборатории. Необходимо построить по имеющимся данным, указанным в таблице 1, контрольную карту средних значений, карту размахов и определить, является ли технологический процесс стабильным.

Таблица 1

№ выборки	X₁	X₂	X₃	X₄	X₅

Задача 2. Контролируется содержание хрома в стальных отливках. В каждую смену проводятся замеры в четырех плавках. В таблице 1 приведены данные по 15 подгруппам (сменам). Построить контрольную карту медиан и карту размахов по результатам измерения хрома в стальных отливках каждой подгруппы. Провести статистический анализ процесса.

Таблица 1

№ подгруппы	Содержание хрома в стальных отливках (замеры)
X1	X2	X3	X4
	0,74	0,76	0,62	0,73
	0,72	0,74	0,84	0,69
	0,87	0,79	0,70	0,92
	0,78	0,66	0,71	0,74
	0,81	0,66	0,82	0,67
	0,63	0,71	0,68	0,82
	0,63	0,73	0,64	0,80
	0,66	0,68	0,85	0,91
	0,63	0,66	0,62	0,85
	0,85	0,61	0,75	0,77
	0,73	0,65	0,74	0,90
	0,85	0,77	0,65	0,69
	0,67	0,69	0,83	0,62
	0,74	0,73	0,62	0,88
	0,81	0,82	0,69	0,73

Задача 3. Компания производит скобы для степлера. Было проведено измерение скоб степлера в 30 подгруппах, с числом выборочных измерений в подгруппе - 6. Полученные данные представлены в таблице 1. Необходимо построить контрольную карту индивидуальных значений по результатам измерения скоб для степлера в подгруппах. Произвести статистический анализ процесса.

Таблица 1

№ подгруппы Ширина скобы, мм.

X1 X2 X3 X4 X5 X6

9,912 9,979 10,043 10,108 9,935 10,009

10,068 9,932 9,952 9,974 9,994 10,057

9,935 10,055 10,008 10,104 10,106 9,967

10,015 10,002 10,036 10,018 9,945 10,138

9,979 9,928 10,065 9,937 10,037 9,972

9,957 9,966 10,012 10,137 9,932 10,043

9,974 10,079 10,07 10,008 10,163 10,069

10,04 9,922 10,051 9,937 9,892 10,029

9,906 10,085 9,919 10,021 10,006 10,183

10,048 9,888 10,099 9,96 10,039 9,954

9,989 10,044 9,997 10,053 9,9 10,074

9,897 9,969 10,098 9,945 9,997 9,905

10,062 10,033 10,139 10,032 9,981 9,99

9,992 10,091 9,939 10,07 9,916 10,118

10,097 9,977 10,024 9,968 10,101 10,177

9,901 10,129 10,061 10,127 9,99 9,931

10,028 10,015 9,908 10,019 10,155 10,112

10,117 9,917 10,082 9,999 10,122 10,051

9,909 10,058 10,116 10,033 9,936 10,072

9,982 9,886 9,928 10,049 9,893 9,949

9,891 9,986 9,92 10,051 9,971 10,157

10,025 10,023 10,005 9,959 9,964 10,013

9,958 10,066 10,127 9,957 10,083 10,016

10,094 9,965 9,934 10,076 9,903 10,068

9,915 10,114 10,089 10,05 10,057 9,968

10,147 9,898 9,976 9,897 9,976 10,187

9,958 10,089 10,118 10,105 10,134 9,945

10,195 10,016 10,054 9,993 9,97 10,098

9,953 10,096 10,047 10,063 10,019 10,004

10,122 9,894 10,134 9,961 10,095 9,896

Задача 4. На производстве пластиковых окон было принято решение улучшить управление качеством операции нарезки штапика. Были собраны и проанализированы данные за 1 месяц. Ежедневно с периодичностью 1 час извлекались случайные выборки (подгруппы) и регистрировалось количество заготовок штапиков, несоответствующих заданному размеру, данные приведены в таблице 1. Необходимо построить контрольную карту доли несоответствующих единиц штапиков по отношению к числу проконтролированных единиц штапиков. Произвести статистический анализ процесса.

Таблица 1

Номер подгруппы	Число проконтролированных единиц (штапиков)	Число несоответствующих единиц (штапиков)

Задача 5. На производстве производят запчасти для автомобиля. Требуется определить стабильность операции сварки автомобильных дверей с применением сварочной машины на предмет соответствия качества сварочного шва требуемым техническим условиям. С этой целью каждый день контролировали 15 операций сварки автомобильных дверей одинакового типа. Данные контроля качества сварки по 14 подгруппам, объемом n=15 каждая приведены в таблице 1. Необходимо построить контрольную карту для числа несоответствий на единицу. Произвести статистический анализ процесса.

Таблица 1

Номер подгруппы	Число несоответствий

ЗАКЛЮЧЕНИЕ

Статистическое управление процессами – это основанное на статистическом мышлении использование как статистических, так и нестатистических методов анализа и решения проблем с целью осуществления действий, необходимых для достижения и поддержания состояния статистической управляемости процессов, и постоянного улучшения их стабильности и воспроизводимости.

Основная задача контрольных карт Шухарта - выявление особых причин изменчивости в ходе технологического процесса за анализируемый период. Для обнаружения признаков особых причин сопоставляют изменчивость внутри подгрупп с изменчивостью между подгруппами. При этом границы оценки изменчивости (контрольные границы) рассчитывают только на основе изменчивости внутри подгруппы. Предполагается, что изменчивость внутри подгрупп обусловливается обычными причинами, а между подгруппами - особыми причинами.

Статистические методы играют важную роль в объективной оценке количественных и качественных характеристик процесса и являются одним из важнейших элементов всего процесса управления качеством. Неслучайно основоположник современной теории менеджмента качества Э.Деминг много лет работал в Бюро по переписи населения и занимался именно вопросами статистической обработки данных. Он придавал огромное значение статистическим методам в управлении процессами.

<2 3 4 5 6 78>

Дата добавления: 2016-03-22; просмотров: 1723;

№ подгруппы	Ширина скобы, мм.
X1	X2	X3	X4	X5	X6
	9,912	9,979	10,043	10,108	9,935	10,009
	10,068	9,932	9,952	9,974	9,994	10,057
	9,935	10,055	10,008	10,104	10,106	9,967
	10,015	10,002	10,036	10,018	9,945	10,138
	9,979	9,928	10,065	9,937	10,037	9,972
	9,957	9,966	10,012	10,137	9,932	10,043
	9,974	10,079	10,07	10,008	10,163	10,069
	10,04	9,922	10,051	9,937	9,892	10,029
	9,906	10,085	9,919	10,021	10,006	10,183
	10,048	9,888	10,099	9,96	10,039	9,954
	9,989	10,044	9,997	10,053	9,9	10,074
	9,897	9,969	10,098	9,945	9,997	9,905
	10,062	10,033	10,139	10,032	9,981	9,99
	9,992	10,091	9,939	10,07	9,916	10,118
	10,097	9,977	10,024	9,968	10,101	10,177
	9,901	10,129	10,061	10,127	9,99	9,931
	10,028	10,015	9,908	10,019	10,155	10,112
	10,117	9,917	10,082	9,999	10,122	10,051
	9,909	10,058	10,116	10,033	9,936	10,072
	9,982	9,886	9,928	10,049	9,893	9,949
	9,891	9,986	9,92	10,051	9,971	10,157
	10,025	10,023	10,005	9,959	9,964	10,013
	9,958	10,066	10,127	9,957	10,083	10,016
	10,094	9,965	9,934	10,076	9,903	10,068
	9,915	10,114	10,089	10,05	10,057	9,968
	10,147	9,898	9,976	9,897	9,976	10,187
	9,958	10,089	10,118	10,105	10,134	9,945
	10,195	10,016	10,054	9,993	9,97	10,098
	9,953	10,096	10,047	10,063	10,019	10,004
	10,122	9,894	10,134	9,961	10,095	9,896