Одновременно необходимо отметить правила, которые должны ответить на следующий вопрос .
Чего мы хотим добиться при анализе поведения затрат их графический отображая и определяя тенденцию?
• Отделение постоянных затрат от переменных
• Линейность или нелинейность
• Причины и влияние зависимостей
• Предсказуемость
2.2.Метод наименьших квадратов.
- поведение затрат.
- Содержание метода
- Тесты на достоверность.
При определении поведения затрат не всегда можно использовать линейную функциональную зависимость. Рассеивание, распределение затрат не всегда подчиняется данной закономерности. Это приводит к использованию различных видов зависимостей, нами приводятся виды и характеристики различных видов однофакторных функции:
| Название функции | Уравнение У=f(x) | Средняя производительность у/х | Предельная производительность dy/dx | Коэффиц. Элластичности E=dy/dx*х/у |
| Линейная | У=а0+а1х | а0 + а1 х | а1 | а1х____ а0 + а1х |
| Квадратная | У=а0+ а1х – а2х 2 | а0 + а1- а 2х х | а1 – 2 а2х | (а1 - 2а2 х ) х а0 + а1х –а2 х2 |
| Кубическая | У=а0+ а1х + а2 х2 –а3х3 | а0 +а1+ а2х – а3х2 х | а1+ 2а2х-3а3х2 | (а1 + 2а2 х –3а3 х2)х а0 + а1х +а2х2 –а3 х3 |
| Гиперболическая | У=а0+а1 х | а0 + а1 х х2 | - а1 х2 | - а1_______ а0 х + а1 |
| Степенная | У= а0 ха1 | а0 ха1-1 | а0 а1 ха1-1 | а1 |
| Показательная | У=а0– kа1 х | а0 – к а1х х | - kа1 хLn а1 | - kа1 хLn а1 а0 – к а1х |
| Экспоненциальная | У=а0еа1х | а0еа1х х | а0а1еа1х | а1х |
Наличие исходных данных и выбранной формы уравнении позволяет перейти к расчету параметров выбранных функции. Существуют различные методы расчета параметров функции, однако практически в большинстве случаев используется метод наименьших квадратов, который позволяет получить параметры функции, удовлетворяющее требованию минимальной суммы квадратов отклонении фактических значении зависимой переменной от вычисленных по уравнению.
Данный метод предусматривает сравнительно простую процедуру вычисления параметров для широкого круга математических функции, если они линейны относительно своих параметров.
В целом функция может быть записана в следующем общем виде:
у = а0 + а1 х1 + а2 х2 + а3 х3 + …+ аn хn ;
здесь х1, х2, … х n может оказаться х, х2, х3, log x, √х, 1х2, х1/х2 и т.д.;
Метод предусматривает минимизацию сумму квадратов отклонении уфакт от урасч.
или же Σ (урасч - уфакт ) 2 = 0
Подставляя значения урасч. получаем
Σ[(а0 + а1 х1 + а2 х2 + а3 х3 + …+ аn хn ) – y] 2 = 0;
Здесь значения х1 , х2 , х3 , … хn и у даны фактическими наблюдениями или получены на основании данных проведенных экспериментов, а значения а1, а2 , а3 … аn являются искомыми параметрами.
В целом общая формула после проведения определенных преобразовании имеет следующий вид:
Σу= nа0 + а1 Σ х1 + а2Σ х2 + а3Σ х3 + …+ аn Σхn ;
Σ х1 у = а0 Σх1 + а1 Σ х12 + а2 Σ х1х2 + … ап Σ х1 х п ;
Σ х2 у = а0 Σх 2 + а1 Σ х1х2 + а2 Σ х22+ … ап Σ х2 х п ;
…………………………………………………………..
Σ х nу = а0 Σх n + а1 Σ х1хn + а2 Σ х 2х n + … ап Σ х п 2;
Для описания теоретических линии зависимостей и для вычисления значения коэффициентов используются различные уравнения .
Например: Для определения коэффициентов линейного уравнения:
Na0 + а 1Σх = Σу;
а 0 Σ х + а 1Σх2= Σху;
Для определения коэффициентов квадратного уравнения :
Na 0 + а 1Σх + а 2Σх2 = Σу;
а 0 Σ х + а 1Σх2 + а 2Σх3 = Σху;
а0 Σ х2 + а1 Σх3 + а 2Σх4 = Σх2 у;
Для определения коэффициентов гиперболайческого ( который чаще всех используется в поведении затрат) уравнения :
na + bΣ 1 = Σу;
х
аΣ х + bΣ 1 2 = Σ 1 2 у; и т.д.
х х
где, n – число наблюдении, которые могут быть заданы в виде годов, месяцев или в качестве изготовляемых единиц и просто периодов наблюдении.
х – переменная, величина которой не зависит от результатирующего показателя;
а, b, или а1, а2 …. а n постоянные коэффициенты вычисляемые с помощью метода наименьших квадратов.
Условия применения метода наименьших квадратов:
1.Линейность математических функции. Вне зависимости от того что, они различны, они должны приводится в линейный вид путем осуществления подстановки. Н-Р : функции х2, х3, х2, х3, log x, √х, 1х2, х1/х2 и т.д., должны заменены на значение х, путем подстановки х= log x и т.д.
2.Применяется в случае, когда модель состоит не из одного уравнения, а представляет систему уравнении. Как было отмечено выше, уравнение должно состоять из целевой - «зависимой» и оказывающее на зависимую показатель воздействие «независимой» величины.
3.Экономическая вероятность. Вероятность изменения целевого значения от воздействия независимых параметров.
4. Предсказуемость.
Пример: 24.8, Друри стр.914
| Месяц | Общие затраты (У), | Выход продукции (Х1) | Число работни-ков (Х2 ), ед. | Труд основных работн. (Х3 ), ч. |
| Сумма | ||||
| Сумма квадрата | 36614,05*106 | 3,8582*106 | 374,423*106 | |
| Сумма Хп * У | 373,5374*106 | 22,81284*106 | 3692,2774*106 |
Ответ:
А) является выход продукции (х1 ).
1. Зависимость линейна т.к. с изменением объема выхода продукции изменяется общие затраты на продукцию.
2. Переменные затраты, как показывают сравнение суммарных затрат занимают значительную часть , т.к. суммарное отношение составляет 637200: 6300=101,1428
Б) См. программу ексель.
| метод абсолютного прироста | TC (Y) | Выпуск (X1) | трудо-часы (X3) | |
| Максимум | ||||
| Минимум | ||||
| Разница | ||||
| B | 75,57894737 | 10,50731707 | ||
| A | 13093,68421 | -8108,97561 |
Метод наименьших квадратов
Таблица регрессионного анализа
Источник: учебник Вильямсона стр. 305
| X | Y | XY | X2 | Y' | (Y - Y')2 | 
|
| Выпуск (X1) | Кол-во работников (X2) | трудо-часы (X3) | х2 расч | х3 расч | ||||||||||
| 39021,73228 | 42134,54 | |||||||||||||
| 43044,09449 | 44660,62 | |||||||||||||
| 43044,09449 | 45808,83 | |||||||||||||
| 47066,45669 | 49483,12 | |||||||||||||
| 47066,45669 | 49827,59 | |||||||||||||
| 56142,77 | ||||||||||||||
| 65167,08661 | 73480,83 | |||||||||||||
| 65167,08661 | 27437,38 | |||||||||||||
| 65167,08661 | 74514,22 | |||||||||||||
| 61144,72441 | ||||||||||||||
| 59133,54331 | 64180,28 | |||||||||||||
| 49077,6378 | 36163,82 | |||||||||||||
| Х2 | х3 | Х2в кв | х3 в квадрате | x*y | x*y | |||||||||
| -17291,3386 | -9305,512096 | |||||||||||||
| 2011,181102 | 11,48215494 | |||||||||||||
Следует отметить, кроме приведенных видов уравнений, которые предусматривает воздействие на результатирующий показатель только одного переменного, существуют и метод предусматривающее одновременного воздействия на целевую (зависимую функцию) множества факторов.
Общий вид данного уравнения выглядит по следующему:
у = а0 + а1 х1 + а2 х2 + а3 х3 + …+ аn хn ;
Это связано в первую очередь
Уравнение регрессии должна объяснить нам, почему у нас есть эта проблема:

Где ‘e’ это остаточный член …
111.Тесты на достоверность. Нам необходима оценить насколько достоверны полученные результаты в результате вычислении. Учитывая то обстоятельство, мы на основании фактических данных вычисляем теоретическую линию зависимостей для определения затрат при прогнозировании, анализе, обоснования управленческих решении и т.д.
Здесь можно воспользоваться следующими тестами на достоверность. Таковыми тестами служат:
ü Коэффициент смешанной корреляции;
ü Среднеквадратические ошибки оценки;
ü Среднеквадратические ошибки коэффициента.
1. Коэффициент смешанной корреляции.
1.1.Теретическая линия, если полностью совпадает с фактическим наблюдениями, она должна находится на теоретической линии, при их графическом отображении.
1.2. При несовпадении линии наблюдения с теоретически вычисленной линией, определяется размер этих отклонении при помощи квадратов разницы.
1.3.Среднее значение этих отклонении между фактическими и линией регрессии в статистике обозначается σи определяется;
| Y' | (Y - Y')2 | 
|
Где,
Υ- фактическое значение ; Υ1 – теоретическое значение ;
Значение теоретического отклонения можно вычислить по следующей формуле:
Σ (Y - Y')2
σ 2=------------------; где N- число наблюдении.
N
1.4.Дисперсия (отклонение) фактических наблюдении от среднего значения, определяемый за исключением отклонения переменных вычисляется по следующей формуле:
Σ (Y - ˉΥ)2
σ 2=------------------; где N- число наблюдении; ˉΥ – среднее значение фактического зависимого
N показателя
1,5. Коэффициент смешанной корреляции:
Σ (Y - Y')2 / N
r 2 = 1 - --------------------- ;
Σ (Y - ˉΥ)2 / N
Коэффициент корреляции. степень связи или теснота связи между рассматриваемыми признаками (r) определяется :
r = √¯ r 2¯
2.Среднеквадратические ошибки оценки.
Необходимость определения:
- теоретическая линия определенная методом наименьших квадратов получена на основании конкретной выборки поэтому возможны отклонения от истинных линии.
- Среднеквадратическая ошибка позволяет определить диапазон значений зависимой переменной (у), в рамках которой есть определенная степень достоверности, т.к. она является мерой отклонения относительно линии регрессии.
- для определения t – распределения ( t –cстатистики), корректировочного значения падающего на недостающее значение тесноты связи.
Абсолютное величина возможного отклонения от линии регрессии определяется с
помощью показателя среднеквадратической ошибки ожидаемого значения, Se, с помощью следующей формулы:
___________
/Σ (Y - Y')2
Se= / ------------------;
√ N -2
Величинаt – распределения ( t –cстатистики) определяется по таблице максимальных значении соответствующее доверительным интервалам с указанными вероятностями.
Степень свободы: Количество наблюдении минус количество переменных в простой регрессии.
3. Среднеквадратические ошибки коэффициента.
Для определения достоверности ожидаемого значения коэффициента регрессии переменных издержек, вычисляется среднеквадратическая ошибка коэффициента b, Sb, по следующей формуле:
Se
Sb= -_--_--_--_--_--_-- ; где, Sb- среднеквадратическая ошибка коэффициента b;
√ [Σ (х -ˉх)2 ]
Упростив данную формулу получаем:
Se
Sb= -_--_--_--_--_--_
√ [Σ х2 -ˉх Σ х ) ]
Например: Для решения можем воспользоваться формулами которые предложены в методических рекомендациях «КАРАНА» (1) и в книге Друри (ст,915) (2):a) Стандартная ошибка
Теперь для примера воспользуемся данными задачи 24,8
| ΣY2 | ΣX1 2 | Σ X2 2 | ΣX3 2 | ΣX1 Y | ΣX2Y | ΣX3Y | |||||
| 36614,05х106 | 3,8582х106 | 374,423 х106 | 373,5374 х106 | 22,81284 х106 | 3692,2774 х106 | ||||||
 (2)
(2)
Стандартная ошибка коэффициента 'b'
 (1)
(1)
 (2)
(2)
При подсчете доверительного интервала используйте:
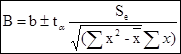
Дата добавления: 2016-03-22; просмотров: 1025;
