Определение объемной газонасыщенности обводненной зоны при отборе газа 3 страница

Выше считалось, что продвижение воды в процессе эксплуатации хранилища пренебрежимо мало. В большинстве случаев это допущение приемлемо и почти не влияет на величину уровня оттеснения пластовой воды, при которой активный объем максимален. Если же активность вод заметная, то при расчетах следует учесть величину К, которая также зависит от /г, но слабо.

При окончательном выборе варианта циклической эксплуатации хранилища следует пользоваться фактической кривой зависимости

Ω = f(h).

ЛЕКЦИЯ №9. О максимально допустимом давлении в хранилище

Активный объем и, следовательно, технико-экономические показатели хранилища существенно зависят от величины максимального давления в нем. Чем оно выше, тем больше активный объем, тем скорей при прочих равных условиях можно заполнить ловушку газом. Однако повышение давления может привести к разрушению покрышки над хранилищем, к уходу газа в вышезалегающие пласты и к прорыву его на дневную поверхность.

При рассмотрении вопроса о максимальном давлении нагнетания газа в водоносный пласт исследователи обычно обращаются к теории гидроразрыва [20].

Признавая правомерность такого подхода, следует, однако, отметить, что вследствие относительно высокой проницаемости пластов, в которых создаются водоносные хранилища газов, а также вследствие небольшой вязкости закачиваемых в пласт газов, реально невозможно создать в призабойной зоне скважин перепады давления, которые могли бы привести к гидроразрыву пласта в обычном понимании этого слова.

При закачке газа в пласт разрывы пород могут произойти под влиянием не столько динамических, сколько статических нагрузок, причем не только вблизи от нагнетательной скважины, но на значительном удалении от нее.

Если покрышка над хранилищем достаточно эластична и непроницаема, с повышением давления в пласте сверх горностатического вышезалегающие породы приподнимутся и пласт расслоится. При этом существенно изменятся условия фильтрации газа, начнется сложный и быстрый процесс перераспределения давления, но все же возможен случай, когда вся толща горных пород будет лежать как бы на газовой подушке. В результате неоднородности и относительно малой пластичности горных пород возможны и разрушения и прорыв газа в вышележащие отложения. Даже небольшая деформация горных пород может привести к обрыву обсадной колонны, а также к нарушению сцепления труб с цементом или цемента с породой. В любом случае появляется реальная угроза аварии (утечка газа из хранилища).

Второй вид разрушения горных пород возникает при наличии в покрышке трещин. Газ проникает в них и при достаточно высоком напоре может преодолеть боковое горное давление, раздвинуть щель и ''уйти'' из пласта-коллектора.

Сила, с которой щель сжимается, зависит от её расположения и от бокового горного давления. Последнее определяется в основном горностатическим давлением и способностью пород передавать вертикальные нагрузки в стороны.

Боковое горное давление составляет долю горностатического давления. Чем ближе расположена трещина к вертикали и чем менее пластичны породы, тем слабей при прочих равных условиях. Она сжимается, тем при меньшем давлении можно нагнетать и хранить газ.

В любой породе можно предполагать наличие небольших зияющих или сомкнутых вертикальных трещин, в которые проникает газ. Вследствие концентрации напряжений в конце щели её развитие не потребует больших дополнительных усилий. При бурении скважин между обсадными трубами, цементом и, породой обычно также остаются микро – и макрозазоры, заполненные глинистым раствором или глинистой коркой. Отсюда следует, что максимально допустимое давление в хранилище следует определять, исходя не из горностатического, а из величины бокового горного давления, и считая, что в покрышке имеются вертикальные трещины. В этом случае можно написать

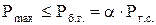(1)

Здесь Рmax – максимальное давление газа в любой точке газового объема; Рб.г. – боковое горное давление; Рг.с. – горностатическое давление

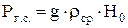(2)

ср. – средняя плотность горных пород

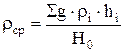(3)

Из уравнений (1) и (2) следует что

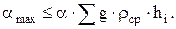(4)

Здесь hi – толщина пород, плотность которых можно считать постоянной.

Коэффициент α в зависимости от угла внутреннего трения горной породы может изменяться в значительных пределах. Для глин коэффициент α можно принимать равным 0,6 – 0,8.

Если известен угол внутреннего трения пород φ, то величину α можно найти по формуле, приведенной в работе [20]

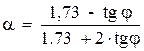(5)

Очевидно, эту формулу можно применять только для пластичных пород, так как при φ >60,4° tg φ >1,73 она теряет смысл.

Учитывая коэффициент запаса, максимально допустимое давление в пласте следует принимать на 30 – 50 % меньше бокового горного давления.

Величину максимально допустимого давления можно определять, исходя и из нормального гидростатического напора, соответствующего глубине залегания хранилища

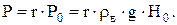(6)

Здесь ρв – плотность пресной воды. В зависимости от степени надежности покрышки, доброкачественности цементажа, и требований технологии хранения газа r принимают в пределах 1,2 – 1,5. В этом случае Рmax = (0,12 – 0,15) Н0, где, Н0 дано в метрах.

В таблице 1 приведены фактические значения для некоторых водоносных газохранилищ бывшего СССР.

Таблица 1. Значения r для некоторых водоносных газохранилищ бывшего СССР

За рубежом максимально допустимое давление в хранилищах находится примерно в тех же пределах, которые указаны в таблице 1.

СПОСОБЫ УВЕЛИЧЕНИЯ АКТИВНОЙ ЕМКОСТИ ХРАНИЛИЩА

При технологическом проектировании часто возникает задача увеличения активного объема хранилища по сравнению с той величиной, которая определяется минимумом приведенных затрат и обычными способами использования ловушки.

Поставленная цель может быть достигнута тремя способами:

1) нахождением такого среднего положения уровня раздела ''газ – вода'', при котором активный объем хранилища будет наибольшим;

2) подбором соответствующего несимметричного режима работы хранилища;

3) снижением давления в водоносном пласте.

Выбор того или иного способа определяется конкретными условиями – формой структуры, гидродинамическими свойствами. Пласта, существующим графиком газопотребления, резервами газотранспортной системы и т. д.

В общем случае следует начинать с простейшего варианта – с нахождения уровня оттеснения вод, при котором активный объем будет наибольшим. Если при этом нужного эффекта достичь не удается, надо рассмотреть возможности изменения режима закачки и отбора газа. Снижение пластового давления следует применять в последнюю очередь.

Зависимость активного объема хранилища от уровня оттеснения

пластовых вод

Предположим, что подвижность пластовой воды рассматриваемого хранилища невелика и изменением объема порового пространства в течение одного цикла можно пренебречь. В этом случае справедлива формула

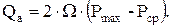(7)

Объем буферного газа определяется по формуле

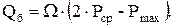(8)

Разделив (7) на (8), получаем:

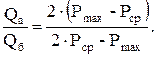(9)

Величина Рср есть начальное пластовое давление водонапорной системы, приведенное к плоскости среднего за год положения раздела ''газ – вода''. По мере снижения среднего уровня этого раздела, т.е. с увеличением количества находящегося в хранилище газа, величина Рср растет и может достигнуть значения Рmax (при этом предполагается, что емкость ловушки не ограничена).

Из выражения (7) видно, что с ростом степени заполнения ловушки газом активный объем хранилища сначала увеличивается за счет быстрого роста Ω, а затем снижается из-за уменьшения до нуля разности Pmax – Pср. Какая-то степень заполнения ловушки газом будет соответствовать максимальному значению активного объема хранилища. Буферный объём газа, как следует из выражения (8), по мере заполнения ловушки газом будет увеличиваться от нуля до максимальной величины Ω Pmax за счет роста Ω и Рср. Чтобы определить, от каких дополнительных параметров и как зависит величина активного объема газа, при каких условиях активный объем газа в хранилище будет наибольшим, рассмотрим ловушку простейшей геометрической формы, например конусообразной (см. схему – 1, тип I). Для такой ловушки связь между объемом порового пространства, занятого газом, и уровнем оттеснения пластовой воды определяется выражением:

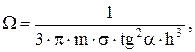(10)

где m – динамическая пористость пласта-коллектора; σ – газонасыщенность;

α – угол наклона пласта к вертикали; остальные обозначения даны на схеме 2.

При отжатии воды статическое давление в хранилище растет по закону

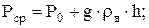(11)

учитывая это, перепишем уравнение (51) в виде

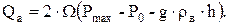(12)

Здесь h – расстояние от наиболее высокой точки пласта на своде поднятия до средней границы раздела газ – вода; Р0 – первоначальное гидростатическое давление в этой точке; ρв – плотность воды.

Подставляя выражение (10) в (12), получим

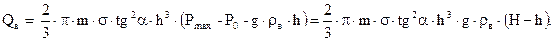(13)

Аналогично для буферного объема будем иметь уравнение:

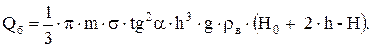(14)

Величину Рmax можно считать постоянной и заданной.

В формуле (14) H = (Рmax – Ро)/ρв – максимальный этаж газоносности, который может быть достигнут при наибольшем допустимом давлении в хранилище.

Взяв производную Qа по h и приравняв её нулю, найдем ту степень оттеснения пластовой воды, при которой в ловушке заданной формы объем активного газа будет наибольшим:

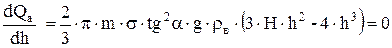(15)

откуда находим, что

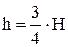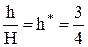или (16)

Здесь h* – относительный этаж газоносности хранилища

Таким образом, в конусообразных ловушках максимальный объем активного газа соответствует оттеснению воды на 3/4 максимально возможной величины, определяемой давлением Рmax. Соотношение между величиной активного и буферного объемов описывается выражением

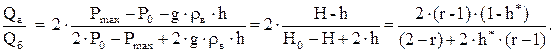(17)

Максимальный объем активного газа для конусовидной ловушки будет при 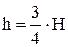, следовательно:

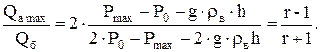(18)

Здесь 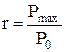коэффициент репрессии.

Подставляя в (57) вместо h величину 3/4·Н, получим:

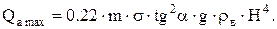(19)

Величина Qa.max сильно зависит от Н. Для рассматриваемого случая она пропорциональна четвертой степени максимальной глубины оттеснения воды в ловушке. Величину Н можно представить в виде:

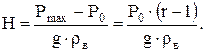(20)

Обычно давление в водоносных пластах подчиняется зависимости, 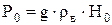следовательно:

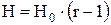(21)

и формула (19) принимает вид:

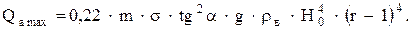(22)

На схеме 2 приведены результаты аналогичных расчетов, выполненных для ловушек других форм. При этом были сделаны некоторые допущения, не влияющие на выводы. В вариантах II и IV принято, что толщина пласта значительно меньше максимальной величины этажа газоносности. В варианте IV считается, что R >> b и R >> r.

Из схемы 2 также следует, что при прочих равных условиях ловушки пластового типа с пологой сводовой частью и крутопадающими крыльями характеризуются большим объемом активного газа, чем ловушки с крутой сводовой частью и пологими крыльями.

В зависимости от формы структуры максимальный объем активного газа пропорционален квадрату, кубу и даже четвертой степени глубины залегания ловушки. Так, с увеличением глубины ловушки первого типа с 300 до 500 м, т. е. в 1,6 раза, Qа увеличивается в 6,5 раза.

Увеличение коэффициента репрессии с 1,30 до 1,50, т. е. в 1,15 раза, для структуры типа I дает прирост максимального объема активного газа в 7,70 раза. Для структуры типа IV такое же изменение r приводит к увеличению

Qа max только в 2,8 раза.

Максимальный объем активного газа практически составляет от одной четверти до одной трети объема буферного газа. Это соотношение заметно увеличивается с ростом коэффициента репрессии. С увеличением относительного этажа газоносности доля активного газа, в общем его объёме монотонно уменьшается. Абсолютная же величина Qа при этом сначала возрастает, а потом при достижении относительным этажом газоносности некоторого критического значения 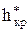падает.

Эксплуатация хранилища при h*> 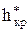явно нецелесообразна, так как при этом уменьшаются и абсолютное значение активного объёма газа и соотношение Qа/Qб.

Из выражения (59) следует, что в ловушках с небольшим относительным этажом газоносности, т. е. в таких, где величиной h по сравнению с Н можно пренебречь, отношение объема активного газа к буферному определяется формулой

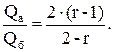(23)

В этом случае отношение активного газа к буферному может достигать большой величины. Так, например, при r = 1,3 отношение 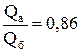, а при

r = 1,7 – .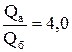

Из приведенных формул следует, что максимальный объем активного газа в зависимости от формы ловушки соответствует оттеснению пластовой воды на 0,5 – 0,75 той наибольшей величины, которую можно получить, исходя из прочности покрышки.

Отношение активного к буферному объему газа уменьшается по мере увеличения относительного этажа газоносности и снижения величины коэффициента репрессии. От формы ловушки это отношение не зависит.

При росте этажа газоносности отношение темпов изменения активного и буферного объемов хранящегося газа изменяется в широких пределах. Наилучшее сочетание активного объема и отношения активного и буферного объёмов газа достигается при работе хранилища на относительном этаже газоносности, несколько меньшем той величины, которая соответствует максимальному значению активного объема газа.

Выше считалось, что продвижение воды в процессе эксплуатации хранилища пренебрежимо мало. В большинстве случаев это допущение приемлемо и почти не влияет на величину уровня оттеснения пластовой воды, при которой активный объём максимален. Если же активность вод заметная, то при расчетах следует учесть величину λ, которая также зависит от h, но слабо.

При окончательном выборе варианта циклической эксплуатации хранилища следует пользоваться фактической кривой зависимости Ω = f(h).

Схема 1.ЗАВИСИМОСТЬ Qа И Qб ОТ УРОВНЯ ОТТЕСНЕНИЯ ПЛАСТОВЫХ ВОД ДЛЯ ЛОВУШЕК РАЗЛИЧНЫХ ТИПОВ

Тип ловушки	I	II	III	IV
Схема ловушки
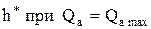
	3/4	2/3	2/3	1/2
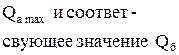
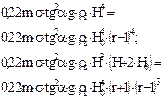
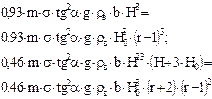
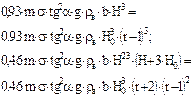
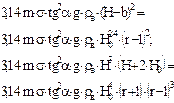
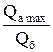
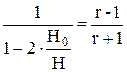
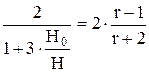
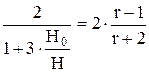
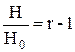
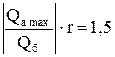
	0,2	0,3	0,3	0,5
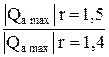
	2,44	1,95	1,95	1,56

ЛЕКЦИЯ №10. Увеличение активного объема хранилищ путем изменения режима их работы

Для стабильной работы хранилища необходимо, чтобы количество воды, внедряющейся в него при отборе газа, было бы равно количеству воды, вытесняемой при закачке газа. Это условие выражается

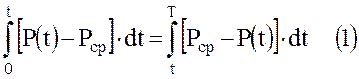
Для газа, находящегося в хранилище, можно написать

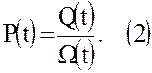
Предположим, что за один сезон вода почти не перемещается. Можно положить Ω = const.

В этом случае график изменения давления в хранилище Р(t) по форме не отличается от графика изменения в нем объема газа Q(t); разница состоит лишь в масштабе, который для объема, газа отличается от масштаба по давлению на величину 1/Q. Это заметно упрощает расчеты, так как графики давления в хранилище выражают собой одновременно и изменение в нем объема газа.

На рисунке 1 показан график работы хранилища. Шкала объемов помещена с правой стороны графика, шкала давлений – с левой.

Рисунок 1. К расчету зависимости Qа от режима работы

хранилища

В рассматриваемом случае условие (1) обозначает равенство площадей S1+S2 = S. Меняя форму площадей, но, соблюдая их равенство, можно получить различные значения активного объема газа. Максимальное давление в хранилище обычно бывает ограничено. Следовательно, ограничена, и высота площади S1. Минимальное давление можно уменьшить, что соответствует увеличению высоты площади S2. Увеличивая площадь S1 за счет её ширины, т. е. времени действия высокого давления, а площадь S2 за счет её высоты, т. е. снижения Pmin, можно, не нарушая условия (1), получить необходимое увеличение активного объема хранилища.

Обозначим исходное минимальное значение давления через Рmin, а измененное 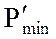, тогда

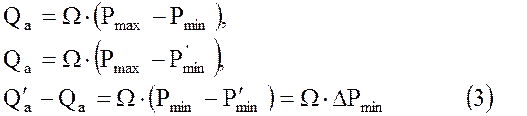
Если учесть влияние подвижности воды, то результат будет несколько отличным от того, который следует из зависимости (66). Из этой зависимости видно, что прирост активного объема хранилища пропорционален уменьшению минимального, давления в хранилище.

На рисунке 1 сплошной линией показан график изменения давления при симметричном режиме закачки и отбора газа, а пунктирной – при несимметричном. Во втором случае активный объем хранилища примерно на 20 % больше, чем в первом, хотя Рmax осталось прежним.

Для соблюдения условия (1) при проектировании режима работы хранилища удобно пользоваться осредненными по месяцам значениями расхода газа.

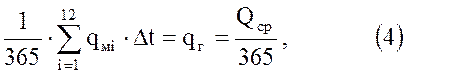
или

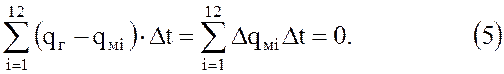
Разделив равенство на qг, получим следующее условие стабильной работы водоносного хранилища:

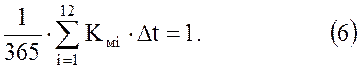
Здесь qмi – средний за i-й месяц расход газа в м3/сут.; Δt – число суток в i-том месяце; Кмi – коэффициент месячной неравномерности для i-го месяца. Уравнение (4) решается методом подбора. В простейших случаях возможно аналитическое определение условий, при которых достигается заданный объем Qa.

Будем считать, что расход газа при его закачке и отборе посто­янный, в конце периодов закачки и отбора имеются нейтральные периоды, когда максимальное давление ограничено (рисунок 2).

Рисунок 2. Циклическая эксплуатация хранилища при условиях qз = const, qo =const и Q= const.

tз – продолжительность периода закачки при постоянном расходе газа qз; tно – продолжительность осеннего нейтрального периода; tо – продолжительность отбора газа при постоянном расходе qo; tнв – продолжительность весеннего нейтрального периода.

В таком случае график периодической асимметричной работы хранилища имеет трапецеидальный вид. Активный объем газа может быть повышен за счет увеличения площади S1 в ширину, а площади S2 по высоте. При этом возрастают расходы газа, так как увеличенный активный объём его приходится закачивать и отбирать за промежутки времени, меньшие, чем при обычном режиме. Мощность КС увеличивается, а срок её работы в течение сезона уменьшается.

Для определения количественных зависимостей между активным объемом хранилища и режимом закачки и отбора газа напишем уравнение:

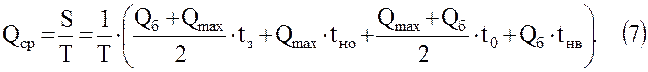
Здесь S – площадь, ограниченная координатами и ломаной линией Q = Q(t).

Выполнив преобразования, зависимость (7) можно привести к виду

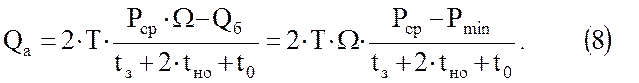
По этой формуле определяется одна из входящих в неё величин При известных остальных.

После подстановки

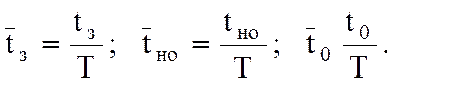
формулу (8) представим следующим образом:

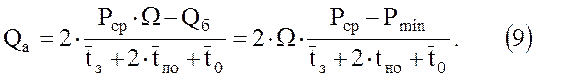
Здесь время закачки, отбора и простоя выражено в долях периода, т. е. в долях года.

Сроки закачки и отбора газа назначаются с учетом условия

t0 + tз + tно + tнв = Т = 365 сут. (10)

В рассматриваемом случае расход газа при нагнетании и отборе является постоянной величиной

Подставляя эту зависимость в формулу (9), находим

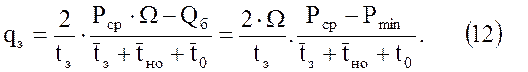
Учитывая далее, что

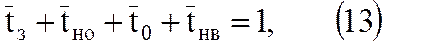
формулы (9) и (12) можно представить следующим образом

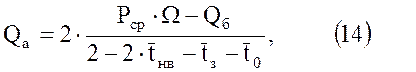
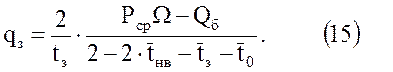
Наибольший практический интерес представляет задача увеличения активного объема в условиях ограниченного объёма порового пространства и заданного максимального давления, т. е. в условиях лимитированной величины Qmax. В этом случае удобней пользоваться следующей формулой:

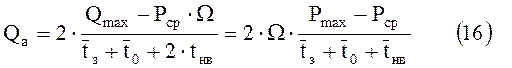
или

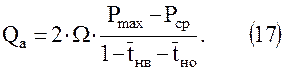
Практически увеличение активного объема газа за счёт режима эксплуатации хранилища сводится к интенсивной его закачке в начале лета и к форсированному отбору газа в конце зимы. Реже удается подкачивать газ в осенне-зимний период и поддерживать в хранилище длительное время, повышенное давление.

Соответствующим подбором режима активный объём хранилища теоретически может быть приближен к Qmax. Однако при этом сильно увеличиваются qз и qо возрастают затраты на сооружение компрессорной станции, бурение эксплуатационных скважин, строительство трубопроводов повышенного диаметра и других сооружений.

В простейшем случае можно использовать метод последовательного приближения и ступенчатого изменения основных показателей режима работы хранилища. Принцип этого метода основан на предположении, что расход оттесняемой из хранилища и втекающей в него пластовой воды пропорционален перепаду, давления в водоносной части пласта.

С. Н. Бузинов показал, что при синусоидальном законе изменения расхода газа расход пластовой воды можно считать по формуле

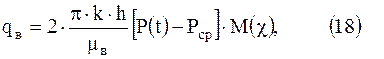
где

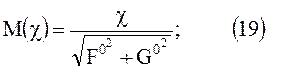
функция М(χ) дана в виде графика представленного на рисунке 3. В нашем случае P(t)=Рф(t). Из (78) Следует, что при циклической работе хранилища

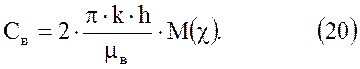
Рисунок 3. Зависимость М = М(χ).

Расчёт состоит в том, что на основе заданной величины Qa и дополнительных ограничений, например по расходу газа или по максимальному давлению, подбирается такой режим работы хранилища, при котором конечные величины Рф (t) и Ω (t) равны начальным, принятым за исходные значения. Если равенства нет, цикл не замыкается и расчеты необходимо повторить, сделав соответствующие коррективы в параметрах режима закачки и отбора газа. При некотором навыке параметры подбирают с первой – второй попытки.

На рисунке 4 приведен график работы Калужского хранилища. За счет применения асимметричного графика закачки и отбора газа из этого хранилища отбирается за сезон 200 – 250 млн. м3 газа, в то время как при симметричном графике активный объем составляет только 160 млн. м3. Следует обратить внимание на то, что интенсивная закачка газа происходит в начале лета.