Определение объемной газонасыщенности обводненной зоны при отборе газа 2 страница
Здесь Qгот – количество газа, используемое в течение года на отопление; Qгио – годовые потребности в газе, за исключением отопления; α – коэффициент, учитывающий, что годовая отопительная нагрузка не полностью входит в активный объем хранилища (эта величина может составлять от 0,4 до 0,8); γ – коэффициент, с помощью которого учитывается повышение расхода газа на технологические нужды; зимой γ составляет примерно 0,01 – 0,02.
Отопительную нагрузку можно более точно оценить, исходя из осредненных климатических и теплотехнических характеристик объектов потребления газа.
При расчетах отопительной нагрузки пользуются понятием ''число градусо-суток''. Обозначив эту величину символом ГС, можем написать, что
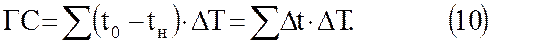
Здесь tо – температура наружного воздуха, при которой не требуется отопления (обычно 16 °С); tн – фактическая среднесуточная температура окружающего воздуха в °С; ΔΤ – число суток, в течение которых среднесуточную температуру можно считать постоянной.
Разность (tо – tн) = Δt называется дефицитом температуры. Она существенно изменяется в зависимости от климатических условий и по годам. Для теплотехнических расчетов используются многолетние средние значения дефицита температуры для данной местности.
При наличии фактических данных о колебаниях потребления газа в зависимости от температуры наружного воздуха прогнозирование зимнего расхода газа значительно облегчается.
С достаточной для практики точностью потребность в газе может быть выражена линейной функцией температуры наружного воздуха
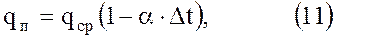
где qср – расход газа при температуре воздуха, когда не требуется отопления помещений, в °С; Δt – дефицит температуры воздуха в °С; а – опытный коэффициент в 1/град.
Величина а колеблется в пределах 0,03 – 0,07 1/град (для Москвы а = 0,065 1/град, для Санкт – Петербурга = 0,059 1/град). Зная qп, производительность хранилища можно определить по формуле
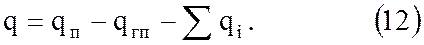
Здесь qгп – производительность газопровода; Σqi – общий дополнительный расход газа (например, за счет регазификации пропана)
ЛЕКЦИЯ №8. Газогидродинамический расчет эксплуатации пластовой части хранилища циклическая эксплуатация водоносного хранилища и определяющие её показатели
Технологическое проектирование эксплуатации хранилища заключается в нахождении оптимального соотношения между основными параметрами, определяющими процесс периодического заполнения хранилища газом и его опорожнения.
В общем случае хранилище состоит из пласта, скважин, шлейфов, компрессорной станции и соединительных газопроводов. Все |эти элементы взаимосвязаны и должны рассматриваться как единая гидродинамическая система, связанная с магистральным газопроводом или непосредственно с потребителем газа. Точное аналитическое решение задачи о движении газа в этой системе затруднено вследствие различия действующих гидродинамических законов, а также существенной нестационарности процессов.
Практически газодинамические расчеты целесообразно вести по отдельным участкам системы, а общее решение получать путем графического совмещения полученных частных результатов. В этой схеме самостоятельно рассматриваются три звена: пластовая часть хранилища; скважины со шлейфами и компрессорная станция с подводящими газопроводами.
Подземные газохранилища предназначаются в основном для покрытия сезонной неравномерности спроса на газ; соответственно работа их носит периодический характер, а длительность периода составляет один год.
На рисунке 1 показан идеализированный график работы подземного газохранилища. Начало координат соответствует началу периода закачки газа.
Закачка начинается весной, в средней полосе обычно в апреле. С повышением сезонной температуры воздуха избытки газа в системе увеличиваются, и темп нагнетания его в хранилище растет (кривая q). К осени расход нагнетаемого газа уменьшается. В октябре – ноябре наступают холода, начинается отбор газа из хранилища.

Рис. 1. График циклической работы водоносного газохранилища.
В водоносном хранилище максимальное и минимальное давления не совпадают с максимальным и минимальным объемом газа в пласте. Это явление называется сдвигом фазы давления. На рисунке1 сдвиг фазы давления обозначен буквой t1. Время на сдвиг фазы в зависимости от свойств пласта и режима работы хранилища может достигать нескольких недель.
При небольшой подвижности пластовых вод геометрический объем газового пузыря в течение года изменяется незначительно и связь между количеством газа, находящегося в хранилище, и. давлением в нем определяется законом Бойля – Мариотта.
Периоды, когда газ не нагнетается и не отбирается, называются нейтральными. Чаще всего они бывают весной и осенью, когда расход газа потребителями соответствует производительности газопровода. Иногда нейтральный период предусматривают, для того чтобы сохранить газ на случай особенно большой в нем потребности.
Газ из хранилища никогда не отбирается полностью. Часть его, остающаяся в пласте к концу периода отбора, называется буферным объемом. Этот объем имеет существенное технологическое и экономическое значение. Чем он больше, тем выше при прочих равных условиях давление в хранилище, тем больше производительность газовых скважин и меньше опасность их обводнения.
Разница между максимальным количеством газа, находящегося в пласте, и буферным объемом газа называется активным или рабочим объемом
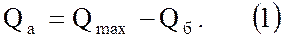
Иными словами, активным объемом хранилища называется та Средняя расчетная часть находящегося в хранилище газа, которая ежегодно отбирается из хранилища и закачивается в него обратно.
Количество газа, отбираемого из хранилища в конкретный год, может отличаться от средней расчетной величины.
При расчетах циклической эксплуатации хранилища различают максимальное, минимальное, среднее и текущее давления, устанавливаемые на основе технико-экономических расчетов. При этом максимальное давление не должно превосходить величины, обусловленной прочностью покрышки.
В водоносном хранилище различают максимальный, минимальный и средний объемы порового пространства, занятого газом. Первая величина имеет значение с точки зрения расширения газового объема и выхода его за пределы ловушки. Вторая – важна, исходя из условия обводнения скважин. Третья величина – чисто расчетная, подобно тому, как и среднее давление в хранилище.
Перечисленные выше технологические характеристики хранилища от года к году могут несколько меняться в соответствии с изменениями спроса на газ, вызванными многолетними колебаниями температуры атмосферного воздуха. Некоторое влияние на показатели могут оказывать также изменения в структуре потребления и подачи газа.
На рисунке 2 схематично изображена связь между давлениями в пласте, объемом газового пузыря и временем при циклической работе хранилища. Предполагается, что среднее давление равно начальному пластовому давлению, приведенному к среднему положению границы раздела газ – вода. Стрелками условно обозначены направления движения пластовой воды.

Рис. 2. Распределение давления в водоносной области пласта при циклической работе хранилища.
Рассмотрим момент времени t1, когда давление в хранилище достигло максимальной величины. В это время газовый объем интенсивно расширяется, так как перепад давления, под влиянием которого находится пластовая вода, максимальный. Объем хранилища расширяется до момента времени t2, когда градиент, давления на границе раздела газа и воды станет равным нулю. По мере дальнейшего снижения давления в хранилище начинает внедряться пластовая вода, хотя давление в нем может быть более высоким, чем начальное давление в пласте.
Наоборот, при заполнении хранилища газом оттеснение воды начинается до того момента, когда давление в хранилище превысит среднюю пластовую величину.
Чем интенсивней изменяется давление в хранилище, тем при прочих равных условиях более заметным будет описанное явление, тем больше разница между Рmах и Рmin, тем меньше отличие rmax и rmin
Площадь овала .1 – 2 характеризует изменение геометрического объема хранилища за счет подвижности пластовых вод. При сокращении периода отбора и закачки газа или при уменьшении подвижности воды ширина овала сокращается и в пределе он вырождается в вертикальную прямую, характеризующую условия Ω = const.
Наоборот, при очень медленном процессе, или при высокой подвижности вод, овал делается более полным и переходит в горизонтальную прямую, выражающую собой условие.
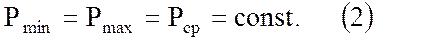
Длина волны давления зависит от продолжительности периода закачки и отбора газа, а также от пьезопроводности пласта. В среднем при годовой цикличности работы хранилища она составляет несколько километров.
Одним из главнейших условий стабильной циклической эксплуатации водоносного газохранилища является равенство количества пластовой воды, внедряющейся в хранилище при пониженном в нем давлении, количеству воды, которое вытесняется из хранилища при повышенном давлении
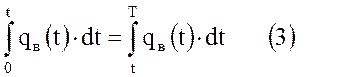
или
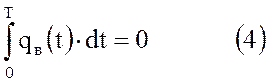
Если это условие соблюдаться не будет, то вода рано или поздно заполнит все хранилище либо, наоборот, будет оттеснена настолько, что «раскроет» ловушку и газ уйдет за пределы последней.
Объем воды, вторгающейся в газовую зону, можно при неограниченном пласте считать пропорциональным перепаду, давления между начальным пластовым давлением Рср, приведенным к средней плоскости раздела газ – вода, и текущим давлением Р(t) на той же плоскости
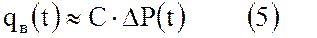
В этом случае условие стабильной циклической работы хранилища можно выразить зависимостью
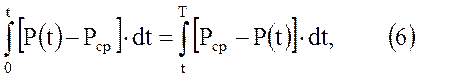
где Т – период, равный году; t – время, в течение которого давление в хранилище ниже средней величины; Т – t – время, в течение которого давление газа в хранилище выше, чем среднее давление, равное начальному, статическому.
Если график закачки симметричен графику отбора, т. е. отличается от последнего только знаком и сдвигом во времени на половину периода, с помощью равенства (6) получим зависимость
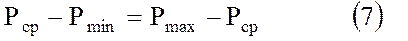
или
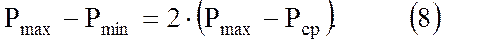
В технологическом проекте устанавливаются следующие показатели эксплуатации хранилища:
I – по пласту.
1. Максимальное, минимальное и среднее давления в газовом объеме пласта: Рmax, Рmin, Рср.
2. Максимальный и минимальный объемы газа в хранилище:
Qmax, Qmin.
3. Максимальный Ωmax, минимальный Ωmin и средний Ωср объемы пор, занятых газом.
4. Максимальный и минимальный уровни оттеснения пластовых
вод в хранилище: Zmax, Zmin.
II – по скважинам.
1. Размещение эксплуатационных, наблюдательных, контрольных и специальных скважин.
2. Предельное значение депрессий и рабочих расходов газа по
эксплуатационным скважинам – ΔPпр и qраб.
3. Максимальный и текущий расходы газа по хранилищу: при отборе газа qmax о и при закачке qmax з.
4. Максимальный расчетный расход пластовой воды, добываемой вместе с газом qв,г.
5. Максимальное и минимальное расчетные давления на забое Рс и на устье скважины Ру при отборе и закачке газа.
6. Максимальное значение расхода газа по скважине при закачке и при отборе газа.
7. Конструкция скважин, в том числе обустройство устья и забоя.
8. Минимальная и максимальная температура газа на устье при закачке и при отборе газа.
III – по наземным сооружениям.
1. Схема обустройства хранилища.
2. Максимальное и минимальное давления до и после регулирующего устройства.
3. Максимальное и минимальное значения давления на приеме и выкиде компрессоров при закачке и при отборе газа.
4. Минимальная и максимальная температура газа до и после штуцера, на приеме и выкиде компрессоров, в конце подводящего газопровода при отборе газа.
5. Максимальная и минимальная температура газа до и после компрессоров, после градирни и в конце шлейфов при закачке газа в хранилище.
Если в технологическом проекте предусматривается применение специальных методов эксплуатации хранилища, то к приведенному выше перечню добавляются показатели, характеризующие технологию этого метода.
РАСЧЕТ ЦИКЛИЧЕСКОЙ РАБОТЫ ПЛАСТОВОЙ
ЧАСТИ ХРАНИЛИЩА
Гидродинамический расчет эксплуатации пористого резервуара, в котором хранится газ, может быть выполнен с помощью различных методик. Наиболее универсальной и хорошо разработанной является методика А. Л. Хейна [47]. Другой способ расчета описан в книге И. А. Чарного с соавторами [51]. Он разработан применительно к горизонтальным пластам, однако приемлем для пологих структур.
Наиболее простым является метод последовательных приближений.
На практике чаще всего используется метод, созданный С. Н. Бузиновым и Е. В. Левыкиным [10]. Многие сложные функции в нем представлены в виде простых безразмерных графиков, использование которых не встречает затруднений. Методика разработана в предположении, что хранилище представляет собой укрупненную скважину постоянного радиуса rф, расположенную в однородном бесконечном пласте постоянной толщины h. Изменением давления в газоносной области хранилища пренебрегают. Газонасыщенность в пределах хранилища принимается постоянной.
Анализ полученных расчетных формул показывает, что эти допущения вполне приемлемы.
Суть метода состоит в том, что расход газа считается заданной периодической функцией времени. При решении этого уравнения совместно с уравнением оттеснения воды из хранилища и с уравнением, описывающим изменение давления в водоносной области при гармоническом возбуждении пласта, находится связь между основными гидродинамическими и технологическими показателями работы пластовой части хранилища. Изменение давления в газоносной части пласта учитывается при последующих расчетах, когда рассматривается работа системы в целом. Схема вывода расчетных формул следующая. Расход газа представляется в виде ряда Фурье:
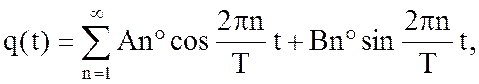 (1)
(1)
где Аn° и Вn° – постоянные коэффициенты ряда Фурье.
Из теории рядов известно, что эти коэффициенты определяются
зависимостями
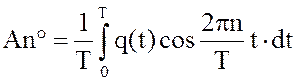 (2)
(2)
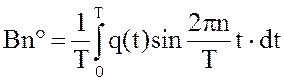 (3)
(3)
Здесь Т – период. В данном случае Т = 1 году. Имея конкретный график закачки и отбора газа, т. е. зная q(t), коэффициенты Аn° и Вn° нетрудно найти численным или графическим путем
С другой стороны, расход газа можно выразить и таким образом:
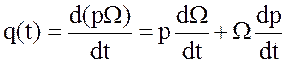 (4)
(4)
Здесь Р – средневзвешенное давление в хранилище; Ω – объем поhjdjuj пространства, занятого газом.
Уравнение (4) нелинейное, решить его трудно. Оно линеаризуется путем подстановки
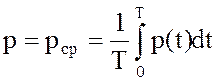
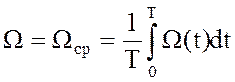 (5)
(5)
В этом случае(4) приобретает вид:
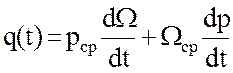 (6)
(6)
Расход воды, оттесняемой в пласт при закачке газа и внедряющейся в хранилище при его отборе, также является периодической функцией времени и выражается рядом Фурье.
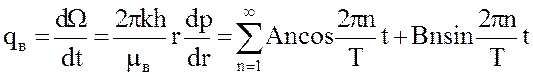 (7)
(7)
Здесь An и Вn – постоянные величины, но в отличие от Аn° и Вn° они неизвестны. Для их определения используется решение задачи о изменении давления в бесконечном пласте, возбуждаемом по гармоническому закону.
Давление на стенке скважины радиусом r при изменении во времени расхода воды по закону (7) выражается зависимостью:
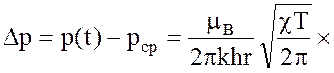
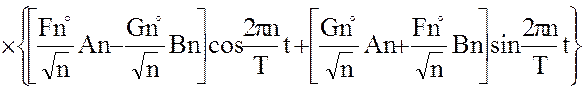 (8)
(8)
Можно показать, что Fn°, Gn°, Аn и Вn являются функциями известного аргумента χ. которые определяются зависимостью
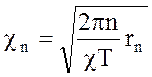 ;
; 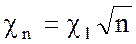 (9)
(9)
Считая, что r = rΦ = rср, выражение можно записать следующим образом:
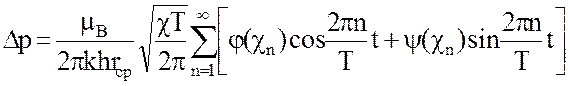 (10)
(10)
Совместным решением уравнений (1), (6) и (10) можно определить все технологические показатели циклической эксплуатации хранилища.
Реальные графики закачки и отбора газа довольно точно могут быть выражены синусоидой вида
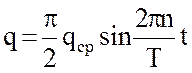 (11)
(11)
Здесь 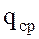 – средний за период закачки или отбора расход газа
– средний за период закачки или отбора расход газа
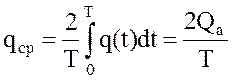 (12)
(12)
В этом случае зависимости (1), (6) и (10) позволяют получить следующие расчетные формулы:
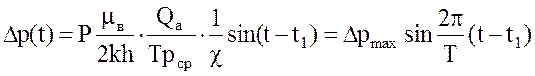 ;(13)
;(13)
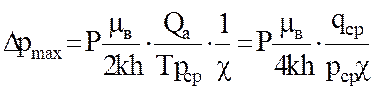 ; (14)
; (14)
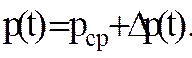 (15)
(15)
Буферный объем определяется зависимостью
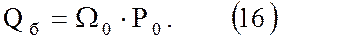
Здесь
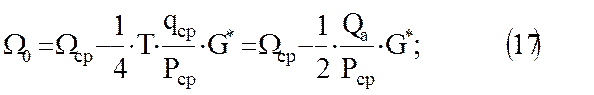


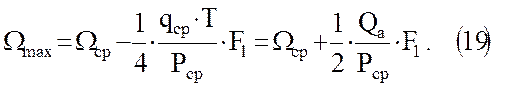
Если задано максимальное давление в хранилище, то для определения Ωmax удобней пользоваться другим выражением
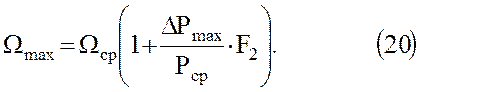
В приведенных зависимостях Р, t1, G*, F2 и F2 являются функциями известных аргументов χ и Ω*, где
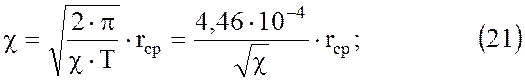
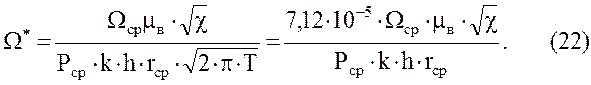
На рисунках 1, 2, 3, 4 и 5 приведены графики, с помощью которых, зная χ и Ω* для конкретных объектов, можно найти функции
t1(χ, Ω*); G*(χ, Ω*); Р(χ, Ω*); F1*(χ, Ω*) и F2*(χ, Ω*).
Обычно известна величина Ωmax. В этом случае Ωср определяется путем подбора.
Поднятия, в которых создается хранилище, иногда осложнены нарушениями или характеризуются литологическими изменениями пласта-коллектора. При этом непосредственное использование приведенных выше формул оказывается неправомерным. Однако в большинстве случаев вполне допустимо пластовую водонапорную систему представлять в виде одного или нескольких векторов с непроницаемыми границами и вести расчеты для каждого из них самостоятельно.
Распределение расходов газа по секторам можно принимать пропорционально произведению их средней гидропроводности на угол при вершине. Соответственно для каждого сектора будут разными величины rcр и Ω*.
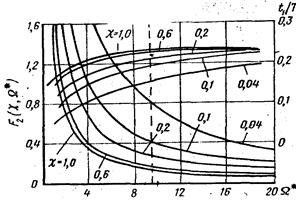
Рисунок 1. Зависимости F2 = F2(χ, Ω*) и t1/Т = f1(χ, Ω*).
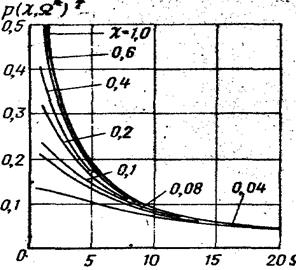
Рисунок 2. Зависимость Р=Р (χ, Ω*).
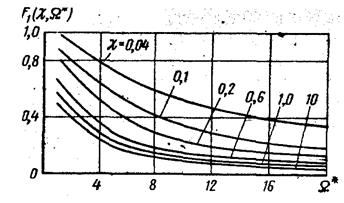
Рис. 3. Зависимость F1 = F2(χ, Ω*)
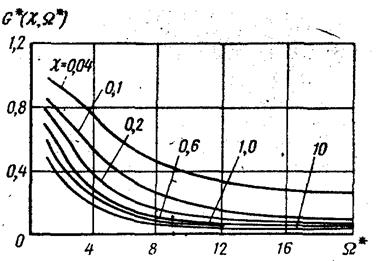
Рис. 4. Зависимость G*= G*(χ, Ω*)
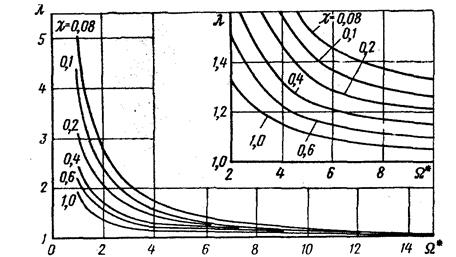
Рис. .5. Зависимость λ =λ(χ, Ω*)
Реальные графики закачки и отбора газа строго не следуют синусоидальному закону, а иногда значительно отличаются от последнего. Однако расчеты, выполненные в работе [10], показывают, что даже при нагнетании и отборе газа с постоянным расходом использование приведенных выше формул не приводит к значительным погрешностям и вполне допустимо.
Выше мы исходим из того, что график нагнетания и отбора газа задан и активный объем известен.
Иногда необходимо решать обратную задачу – определять активный объем хранилища по давлению в нем и по объему порового пространства. В этом случае можно воспользоваться уравнением (14), выразив в нем qср через активный объём.
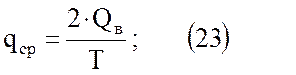
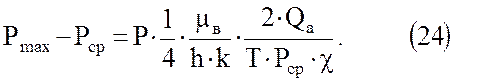
Но так как
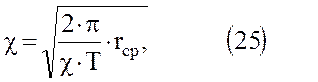
зависимость (24) можно представить следующим образом:
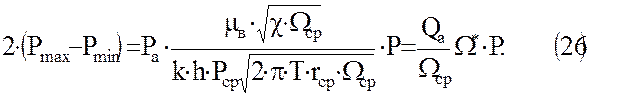 Замечая, что
Замечая, что
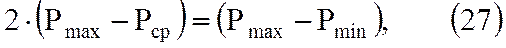
можно написать
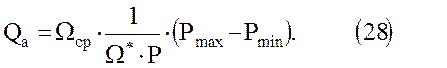
Обозначив далее 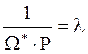 , окончательно получим
, окончательно получим
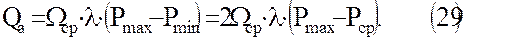

Здесь λ показывает долю изменения среднего геометрического объёма хранилища за счёт продвижения пластовых вод. На рисунке 5 приведен график зависимости, где
λ = λ(χ,Ω*) (30)
Из приведенного на рис. 5 графика следует, что активный объем газа при достаточно подвижной воде может быть в 2 – 3 раза и более выше, чем при газовом режиме. Однако чаще подвижность воды не очень высока и λ составляет 1,1 – 1,2.
Если величина коэффициента подвижности λ еще меньше (λ 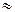 1), то формула (29) будет иметь следующий вид:
1), то формула (29) будет иметь следующий вид:
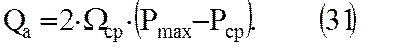
При небольшой подвижности пластовых вод давление в хранилище достигает минимума к концу отбора газа и тогда
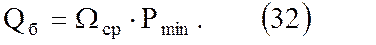
К концу закачки газа
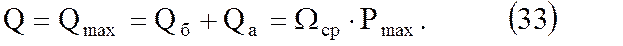
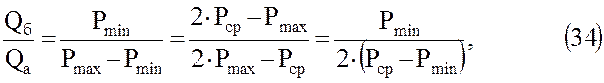
так как
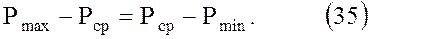
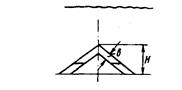
| СХЕМА ЗАВИСИМОСТЬ Qа И Qб ОТ УРОВНЯ ОТТЕСНЕНИЯ ПЛАСТОВЫХ ВОД ДЛЯ ЛОВУШЕК РАЗЛИЧНЫХ ТИПОВ | ||
| Тип ловушки | I | |
| Схема ловушки | 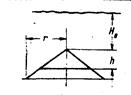
| 
|
| h* при Qа=Qа.max | 3/4 | 2/3 |
| Qа.max и соответ. значение Qб | 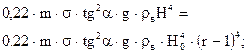 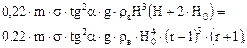
| 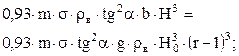 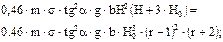
|
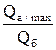
| 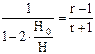
| 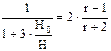
|
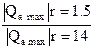
| 2.44. | 1,95 |
продолжение схемы
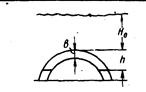
| Тип ловушки | III | IV | |
| Схема ловушки | 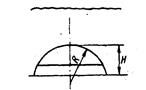
| 
| |
| h*при Qa = Qa max | 2/3 | 1/2 | |
| Qa max и соответствующее значения Qб | 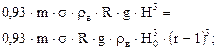
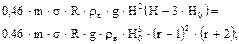
| 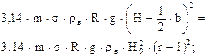
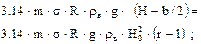
| |
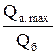
| 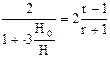
| 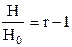
| |
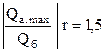
| 0,3 | 0,5 | |
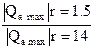
| 1,95 | 1,56 |
В зависимости от формы структуры максимальный объем активного газа пропорционален квадрату, кубу и даже четвертой степени глубины залегания ловушки. Так, с увеличением глубины ловушки первого типа с 300 до 500 м, т. е. в 1,6 раза, Qа увеличивается в 6,5 раза.
Увеличение коэффициента репрессии с 1,3 до 1,5, т. е. в 1,15 раза, для структуры типа I дает прирост максимального объема активного газа в 7,7 раза. Для структуры типа IV такое же изменение г приводит к увеличению Qa.max только в 2,8 раза.
Максимальный объем активного газа практически составляет от одной четверти до одной трети объема буферного газа. Это соотношение заметно увеличивается с ростом коэффициента репрессии. С увеличением относительного этажа газоносности доля активного газа в общем его объеме монотонно уменьшается. Абсолютная же величина Qа при этом сначала возрастает, а потом при достижении относительным этажом газоносности некоторого критического значения и* падает.
Эксплуатация хранилища при h* > hкр* явно нецелесообразна,
так как при этом уменьшаются и абсолютное значение активного объема газа и соотношение Qа/Qб.
Из выражения (59) следует, что в ловушках с небольшим относительным этажом газоносности, т. е. в таких, где величиной h по сравнению с Н можно пренебречь, отношение объема активного газа к буферному определяется формулой
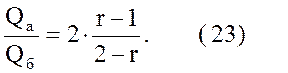
В этом случае отношение активного газа к буферному может достигать большой величины. Так, например, при r = 1,3 отношение Qа/Qб.= 0,60 – 0,86, а при r = 1,7 отношение Qа/Qб.= 4,0.
Из приведенных формул следует, что максимальный объем активного газа в зависимости от формы ловушки соответствует оттеснению пластовой воды на 0,50 – 0,75 той наибольшей величины, которую можно получить, исходя из прочности покрышки.
Отношение активного к буферному объему газа уменьшается по мере увеличения относительного этажа газоносности и снижения величины коэффициента репрессии. От формы ловушки это отношение не зависит.
При росте этажа газоносности отношение темпов изменения активного и буферного объемов хранящегося газа изменяется в широких пределах. Наилучшее сочетание активного объема и отношения активного и буферного объемов газа достигается при работе хранилища на относительном этаже газоносности, несколько меньшем той величины, которая соответствует максимальному значению активного объема газа.
Дата добавления: 2016-03-22; просмотров: 1182;
