Лекция 4. Метод конечных разностей. Метод граничных
Элементов
Для приближенного решения задач теплопроводности и некоторых задач газовой динамики широко применяется метод конечных разностей (метод сеток). В нем область непрерывного изменения функциональной зависимости заменяется расчетной сеткой – дискретным множеством точек (узлов).
Частные производные, входящие в дифференциальные уравнения и граничные условия, заменяются разностными соотношениями. В результате такой замены решение задачи в частных производных сводится к решению системы разностных алгебраических уравнений. Несмотря на то, что число неизвестных в этой системе значительно, решение ее упрощается, а с применением ЭВМ не вызывает проблем.
Пусть температура тела изменяется от a = 100 °C до b=500 °C. При равномерном разбиении интервала имеем: xi = a+ih, где
i = 0, 1,..., N+1, а 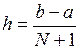 .
.
Пусть некоторая функция f(x) = u является аналитической, разложим ее в ряд Тейлора в окрестностях точки xi.
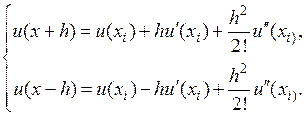
Сложив оба выражения, получим изменение функции в узле i.
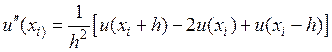 ,
,
а если вычтем, то получим с точностью до более высокого порядка малости: 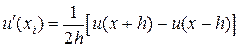 .
.
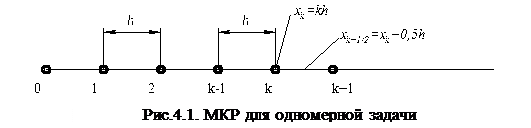 |
Для одномерной задачи имеем:
Для двумерной величины получаем сетку на плоскости: с шагом h по оси х и h по оси y.
В точках задаются граничные условия:
u(x=k=0)=a; u(x=k=N+1)=b
или значения u0 и uN+1 определяются из граничных условий.
При использовании метода МКР нужно выбирать правильно шаг сетки и вид шаблона. Под шаблоном понимают множество узловых точек, значения в которых используются для аппроксимации производной в одной конкретной точке.
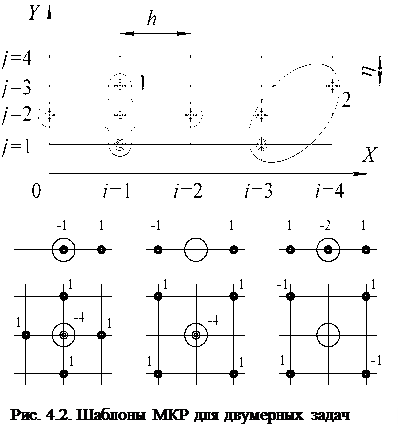 Примеры шаблонов для одномерных и двумерных задач приведены на рис. 4.1 и 4.2. Кружком большего диаметра обозначены узлы, в которых аппроксимируется производная. Черными точками обозначены узлы, значения переменной в которых входят в вычисление искомой производной. Числа около узла – это коэффициент, с которым значение переменной узла входит в шаблон вычисления. Для одномерных шаблонов (см. рис. 4.1) показана аппроксимация производных
Примеры шаблонов для одномерных и двумерных задач приведены на рис. 4.1 и 4.2. Кружком большего диаметра обозначены узлы, в которых аппроксимируется производная. Черными точками обозначены узлы, значения переменной в которых входят в вычисление искомой производной. Числа около узла – это коэффициент, с которым значение переменной узла входит в шаблон вычисления. Для одномерных шаблонов (см. рис. 4.1) показана аппроксимация производных 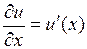 в точке К.
в точке К.
На рис. 4.2 показаны шаблоны для двумерных задач: 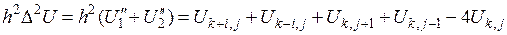 ;
;
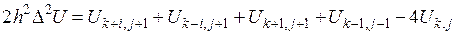 ;
;
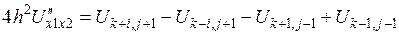 .
.
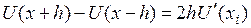 ,
, 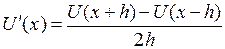 – центральная разность.
– центральная разность.
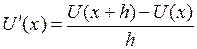 – правое разностное отношение.
– правое разностное отношение.
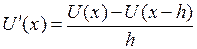 – левое разностное отношение.
– левое разностное отношение.
Метод граничных элементов (МГЭ) отличается от метода конечных элементов (МКЭ) тем, что он позволяет решать задачи с использованием дискретизации лишь границы области. В то время как МКЭ и МКР требуют дискретизации всей расчетной области и расчет проводится с определением значений функции на всех узлах сеток, в МГЭ предусмотрен предварительный переход от исходной краевой задачи для дифференциальных уравнений, описывающих процесс, например, теплопередачи или НДС детали к соотношениям, связывающим функции на границе области. Эти соотношения представляют собой граничные интегральные уравнения или особые функционалы. При этом число узлов уменьшается в два и более раз, возникает возможность выполнять расчеты для бесконечных областей, а также для решения задач, имеющих трещины, вычислять колебания волн в заливе и т.п. Однако данный метод пока наиболее эффективен для двумерных областей (на плоскости).
Дата добавления: 2016-02-16; просмотров: 1418;
