Коэффициенты запасов прочности для типовых деталей ДВС
| Деталь | Материал детали | Диапазон [n] для МКЭ | Диапазон [n] для инженерных методик |
| Блок-картер | Сталь 20, 20Л | 1,8...2,2 | 3,5…5 |
| Чугун ЧШГ | 1,9…2,2 | 4…5 | |
| Коленчатый вал | Сталь (кованая) | 1,6…1,9 | 3,5…5 |
| Чугун (ЧШГ) | 1,7…2,0 | 3,5…4 | |
| Поршень (головка) | Сталь | 1,5…1,9 | 3…4 |
| Чугун | 1,6…2,0 | 3,5…4 | |
| Поршень (тронк) | Алюмин. сплав (АК) | 1,4…1,7 | 3…3,5 |
| Поршневой палец | Сталь (ГОСТ 4543-71) | 1,6…2,0 | 3,5…4 |
| Шатуны | Сталь (ГОСТ 4343-71) | 1,6…2,0 | 3,5…4 |
| Втулка цилиндра | Чугун (ХНМ) | 1,5…1,8 | 3…4 |
| Головка цилиндра | Чугун (ЧШГ) | 1,4…1,6 | 3…3,5 |
Все эти сведения нужны при расчетах напряжений по инженерным методикам. При квалифицированных расчетах МКЭ автоматически учитываются и масштабный фактор, и концентрация напряжений, и поверхностная обработка, и особенности нагружения в эксплуатации, поэтому коэффициенты запаса n для типовых деталей ДВС берут из табл. 2.3.
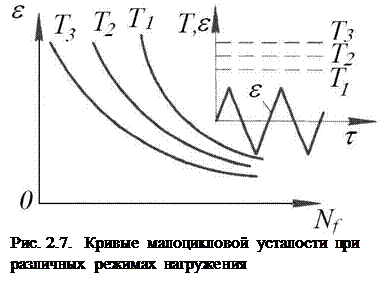
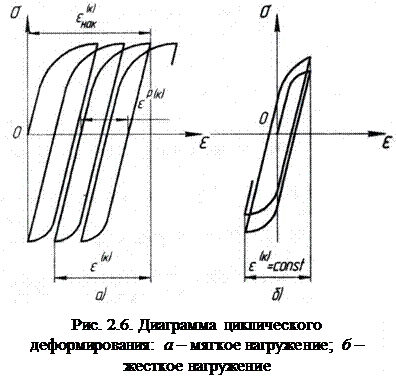 Детали форсированных двигателей работают в условиях переменных по длительности циклов нагружения с выдержками при максимальной температуре, что приводит к резкому уменьшению числа циклов до разрушения. Могут возникать неизотермически мягкое (рис. 2.6, а) и неизотермически жесткое (рис. 2.6, б) нагружения. При высоких циклических температурах появляется малоцикловая усталость (рис. 2.7), которая резко снижает долговечность вследствие возникающих процессов ползучести в материале.
Детали форсированных двигателей работают в условиях переменных по длительности циклов нагружения с выдержками при максимальной температуре, что приводит к резкому уменьшению числа циклов до разрушения. Могут возникать неизотермически мягкое (рис. 2.6, а) и неизотермически жесткое (рис. 2.6, б) нагружения. При высоких циклических температурах появляется малоцикловая усталость (рис. 2.7), которая резко снижает долговечность вследствие возникающих процессов ползучести в материале.
 В этих случаях необходимо решать упругопластические задачи. На практике эти задачи решаются двумя методами – с применением метода переменных параметров упругости или с использованием теории ползучести.
В этих случаях необходимо решать упругопластические задачи. На практике эти задачи решаются двумя методами – с применением метода переменных параметров упругости или с использованием теории ползучести.
В случае многоосного напряженного состояния обычно используют энергетические условия начала пластической деформации Максвела – Хубера s i= sт, по которому пластическая деформация возникает при интенсивности напряжений si, достигающей предела текучести при растяжении sт. Здесь по теории малых упругопластических деформаций изменение деформаций от напряжения рассматривается в виде обобщенного закона Гука:
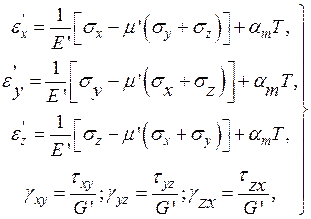 (2.19)
(2.19)
где Е,G – модули упругости материала первого и второго рода; m, aт – соответственно коэффициент Пуансона и коэффициент линейного расширения; Т – изменение температуры в рассматриваемой точке детали. Принимается, что параметры упругости E¢, G¢, m¢ являются переменными для каждой точки тела и определяются следующими зависимостями:
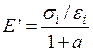 ;
; 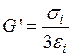 ;
;  , где
, где 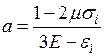 . (2.20)
. (2.20)
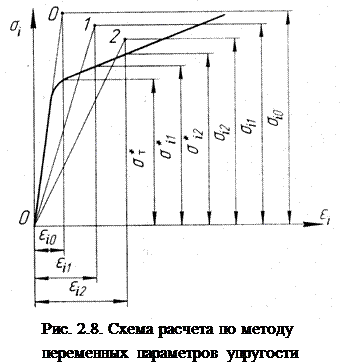 На рис. 2.8 схематично показан процесс последовательных приближений при решении упругопластической задачи. Вначале по формулам (2.12) и (2.13) вычисляются интенсивности деформаций ei0 и напряжений si0. В первом приближении величина точки 01 заменяется на
На рис. 2.8 схематично показан процесс последовательных приближений при решении упругопластической задачи. Вначале по формулам (2.12) и (2.13) вычисляются интенсивности деформаций ei0 и напряжений si0. В первом приближении величина точки 01 заменяется на
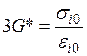 (
( 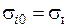 ), при этом интенсивность напряжений равна
), при этом интенсивность напряжений равна 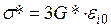 ;
;
E= 3G*;
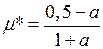 ,
,
а s*=sт материала.
Ползучесть
Основные детали двигателя, в том числе детали цилиндро-поршневой группы, работают при повышенных температурах. При этом в конструктивных материалах проявляются свойства ползучести и длительной прочности.
Под ползучестью понимают пластическую остаточную деформацию детали в зависимости от рабочей температуры, действующих нагрузок и времени. При этом в связи с протекающими остаточными деформациями в детали уменьшаются усилия, которые вызвали деформацию, и дальнейшая деформация при данной температуре прекращается. Это явление называется релаксацией напряжений. Оба процесса обычно происходят одновременно. На рис. 2.9 показаны деформации ползучести сплава АК4-Т, который часто применяется для поршней, для различных случаев приложения нагрузок.
В кривой ползучести можно выделить три участка (рис. 2.9, а – участок упругого деформирования не учитывается): I – участок, где скорости деформирования за счет упрочнения уменьшаются до скорости, которая сохраняется на протяжении второй стадии деформирования (II – участок), на третьем участке (III) скорость ползучести возрастает и заканчивается разрушением, причем при вязком разрушении образуется шейка на образце растяжения, а при хрупком – образуются внутренние трещины. Для вязкоупругих материалов кривая ползучести сохраняет свой вид и при постоянном нагружении, и при пульсирующем, или синусоидальном, переменном во времени нагружении. Исследования О.В. Соснина, Б.В. Горева, А.Ф. Никитенко [5] показали, что продолжительность процесса ползучести не зависит от чередования и времени приложения к образцу нагрузок и температур, а зависит от общей работы разрушения (или разупрочнения), которая определяется площадью под кривой ползучести (рис. 2.9, а – площадь заштрихована).
В общем случае скорость разрушения вязкоупругого материала в процессе ползучести может быть описана уравнением
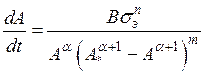 , (2.21)
, (2.21)
где A* – энергия разрушения данного материала;
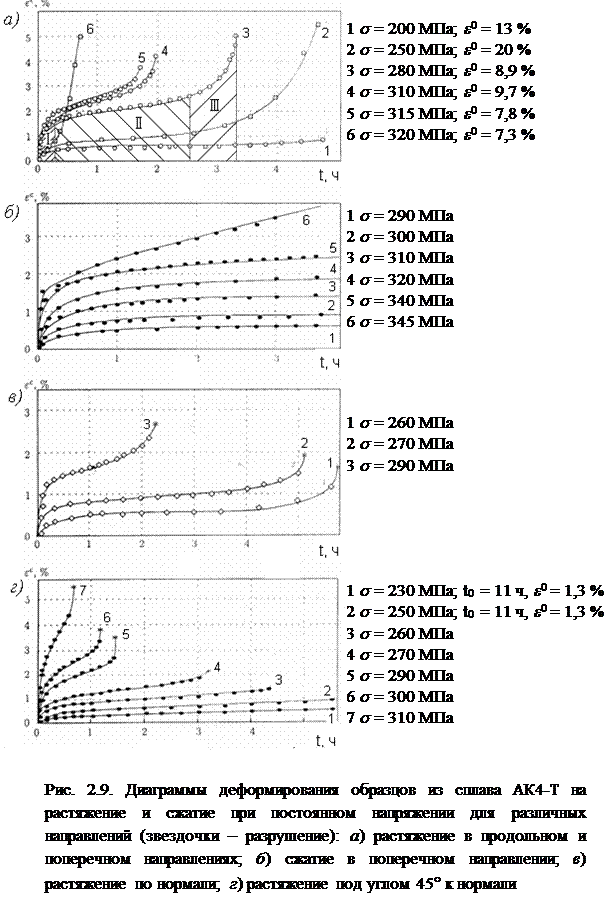
sэ – эквивалентное напряжение
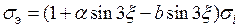 . (2.22)
. (2.22)
Константы b, a и b определяются из экспериментальных данных: x= 0 при кручении, x= 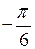 при растяжении, x=
при растяжении, x= 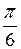 при сжатии.
при сжатии.
Энергетический вариант теории ползучести позволяет определять долговечность деталей ДВС с учетом истории нагружения, учитывающей любые изменения температурно-силового диапазона, и совпадает с теорией длительной прочности. Под длительной прочностью понимают время в часах, в течение которого материал выдерживает нагрузку при заданных температуре и напряжениях. Например,
сталь 40Х10С2М при 550 °С выдерживает нагрузку sдл = 24кг/мм2 в течение 100 ч (табл. П.10).
Дата добавления: 2016-02-16; просмотров: 1508;
