Лекция 3. Численные методы исследования напряженно-деформированного состояния деталей ДВС. Метод конечных

Элементов

Описание физико-химических процессов, протекающих в двигателе внутреннего сгорания и его элементах, базируется на основных законах сохранения массы, энергии и количества движения, описываемых системами дифференциальных уравнений в частных производных. Моделирование может вестись по временной и по пространственной переменным. Решить поставленную задачу позволяет применение численных методов с использованием современных ЭВМ.

К наиболее распространенным способам численного решения систем дифференциальных уравнений ДВС относятся метод конечных разностей (МКР) и метод конечных элементов (МКЭ). В последнее время начинает применяться еще метод граничных элементов (МГЭ). Рассмотрим только основные идеи этих методов, и затем каждый из вас в процессе выполнения курсового проекта попробует сделать расчет напряженно-деформированного и теплового состояния цилиндропоршневой группы.

В основе МКЭ лежит дискретизация расчетной области с целью определения напряженно-деформированного состояния в любой точке области на основе решения систем уравнений механики сплошной среды. При этом основные этапы метода конечных элементов состоят в следующем:

1. Рассматриваемая область разбивается на конечное число подобластей – конечных элементов. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют всю форму области. Векторы внешних нагрузок прикладываются к узлам на границе области.

Таблица 3.1

Функции формы

Название конечного элемента	Число узловых точек	Функции формы Ni конечного элемента в естественных координатах
Стержневые:
симплекс-элемент			y(x)=a1+a2x
квадратичный элемент			y(x)=a1+a2x+a3x2
Плоские элементы:
треугольный элемент		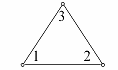	u(x) = a0 + a1x + a2y
четырехугольный элемент			u(x) = a0 + a1x + a2y + a3xy
треугольный изопараметрический элемент		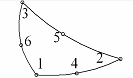	u(x) = a0 + a1x + a2y + a3x2 + + a4y2 + a5xy
четырехугольный изопараметрический элемент		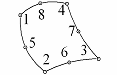	u(x) = a0 + a1x + a2y + a3xy + a4x2 + a5y2 + a6xy2 + a7x2y.
Объемные или трехмерные элементы:
осесимметричный элемент		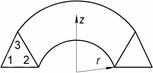	u(x)=a0+a1r+ a2z
тетраэдальный элемент		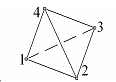	u(x) = a0 + a1x + a2y + a3z
призматический шестигранный элемент		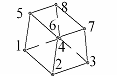	u(x) = a0 + a1x + a2y + a3z+ +a4xy+ a5yz+ a6zx+ a7xyz
изопараметрический шестигранный элемент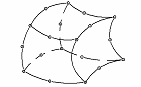

2. Исследуемая непрерывная функция в каждой узловой точке считается неизвестной, подлежащей дальнейшему определению.

3. Непрерывная величина функции аппроксимируется на каждом элементе с помощью выбора определенного набора функций, вид которых зависит от типа элемента и количества узловых точек, входящих в него. Полиномы подбираются таким образом, чтобы непрерывность функции сохранялась вдоль границы элемента.

Представленные уравнения конечных элементов называются функциями формы (табл. 3.1). Они значительно упрощаются, если ввести локальную систему координат с пределами изменения переменной . Тогда поле перемещений D = [u, v, w] в изопараметрических конечных элементах задается через функции формы элемента, которые собираются в матрицу [N], т.е. D=N{d}, где {d_ij} – узловые перемещения.