Понятие о матрице жесткости

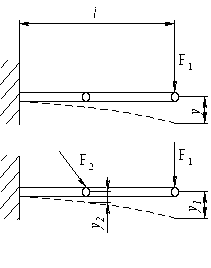Рассмотрим консольную балку, нагруженную силой F₁ на конце. Вертикальные перемещения точки приложенной силы равно 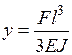, где Е – модуль упругости; J – момент инерции поперечного сечения балки. Если перемещение y задано, то сила 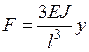или F= Ky, где

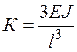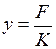и . (3.1)

Величина K называется коэффициентом жесткости. K – есть сила, которую надо приложить на конце балки, чтобы прогиб был равен единице. Пусть на балку действует еще вторая сила F₂, тогда

y₁=d₁₁F₁+d₁₂F₂; y₂=d₂₁F₁+d₂₃F₂, (3.2)

где d₁₁ – перемещение в направлении y₁ под действием единичной силы, направленной по F₁, величины d_ij называют коэффициентами влияния и они зависят от геометрических характеристик балки и от модуля упругости.

Поле перемещений равно в общем случае Y=DF. (3.3)

Тогда в матричной форме: 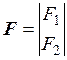; 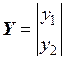, а 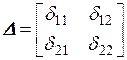– матрица податливости. Заметим, что матрица податливости симметрична, так как d₂₁ = d₁₂ по теореме Максвелла о взаимности перемещений.

Если перемещения известны, то из F = D^-1Y можно найти силы, но F = K Y, тогда K=D^-1, т.е матрица жесткости будет равна обратной матрице податливости. Переходя к объемным конечным элементам, имеем:

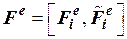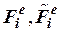Вектор нагрузок , где – матрицы сил узлов i, j, ..., причем 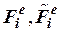– поверхностные силы и эквивалентные поверхностным напряжениям узловые силы, а также объемные силы. 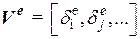– вектор приращений перемещений от нагрузок.

Силы 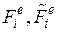будем считать эквивалентными действующим нагрузкам т.е. KV^e=F^e, где матрица жесткости имеет вид

.

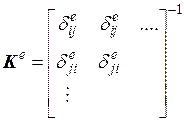В основу МКЭ положен вариационный принцип Лагранжа, в соответствии с которым равновесное состояние, в которое может перейти твердое тело под действием приложенных сил, характеризуется минимумом потенциальной энергии.

Полная потенциальная энергия всей системы равна деформации телаЭи работы массовых и поверхностных сил.

Для установившегося состояния можно записать

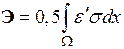, (3.4)

где e¢ - матрица относительных деформаций; s – матрица напряжений; x – матрица рассматриваемой области твердого тела; W – вся рассматриваемая область тела.

Деформации e_у можно выразить через перемещения с помощью уравнений Коши

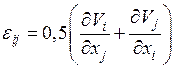, (3.5)

где V_i– перемещение по оси Х_i или в матричной форме

e=0,5[D][V], (3.6)

где D – оператор дифференцирования уравнений Коши; [V] - матрица перемещений точек тела.

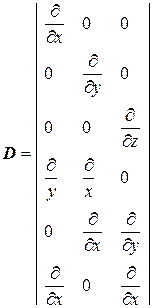. (3.7)

Деформация и напряжения связаны между собой с помощью матрицы Е, характеризующей упругие свойства среды:

s=[E][e] , (3.8)

где

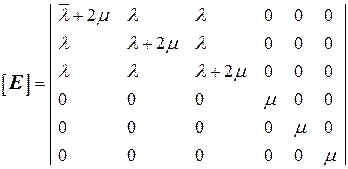, (3.9)

l, m – множители Ляме.

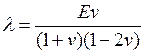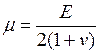; . (3.10)

E – модуль упругости тела; n – коэффициент Пуансона, при этом модуль сдвига G=0,5 E/(1+n).

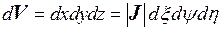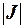, – определитель матрицы Якоби.

Если якобиан равен 0, то элемент вырожденный, необходимо повторить разбиение на элементы, чтобы не было нулевых.

Подставляя (3.8) и (3.6) в (3.4), получаем

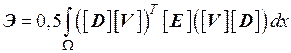(3.11)

Или можно записать

,

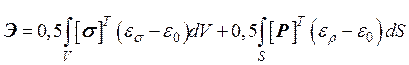где s - объемные силы; Р – внешние поверхностные силы; e_s –деформации от s; e_р – деформации от поверхностных сил Р.

Решение задачи дает поле перемещений V(x). Это решение аппроксимируется с помощью координатных функций формы N и неопределенных коэффициентов Q.

Матрица перемещений U(x)=[N][Q]. (3.12)

Заменяя в (3.6) V(x) на U(x), получим

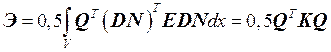, (3.13)

где 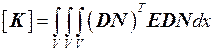– матрица жесткости.

Дифференцируя (3.4) находим

KQ=B, (3.14)

где 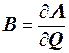– вектор нагрузок и задача анализа прочности в МКЭ свелась к решению системы линейных алгебраических уравнений (3.5).

Задачу определения вектора Q неопределенных коэффициентов системы решают или методом коллокаций, или методом наименьших квадратов, или методом Галеркина, с помощью которых минимизируются невязки в среднем по области интегрирования. При этом после замены функции перемещения V(x) аппроксимирующим выражением N(x)Q в исходном дифференциальном уравнении Ляме

,

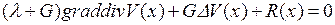где D – дифференциальный оператор 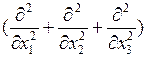, применяемый по всем элементам вектора V(x); R(x) – вектор массовых и приложенных сил. Матрица жесткости обычно сильно разрежена, поэтому для решения (3.5) применяют методы решения разреженных матриц (метод Гаусса, метод Халецкого и др.).

Применение МКЭ сводится к следующим операциям:

1. Создание геометрической модели исследуемой среды (детали) путем геометрического моделирования или вручную на экране дисплея.

2. Выбор из библиотеки модели КЭ, задание внешних нагрузок и значений геометрических и физических параметров и граничных условий.

3. Создание в геометрической модели сетки конечных элементов с определением координат условных точек.

4.

5. Объединение всех конечных элементов в единую конечно-элементную модель детали. При объединении элементы матрицы K образуются суммированием тех элементов матриц жесткости K_i, отдельных КЭ, которые относятся к одному и тому же узлу и направлению перемещения.

6. Решение системы уравнений (3.14).

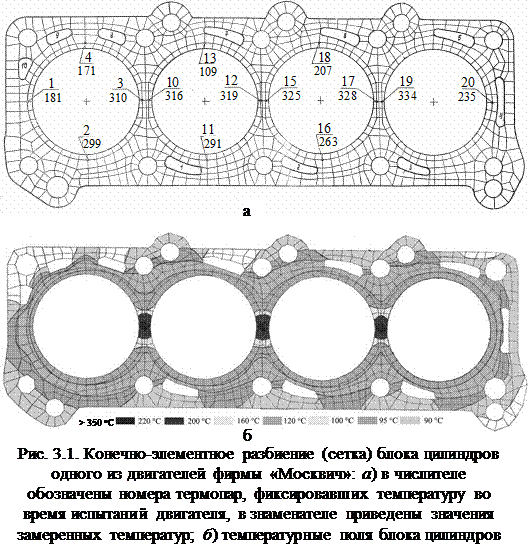
7. Представление результатов решения либо в виде деформированной детали, либо распределения интенсивности напряжений или температур в виде гаммы цветовой окраски.