РАСЧЕТ ЛОГИЧЕСКОГО УСТРОЙСТВА
В системе управления электромагнитным тормозом двигателя, для фрагмента которого известна формула переключательной функции FX , определяющей условия включения тормоза в зависимости от состояния трех различных датчиков положения "А", "В" и "С"
FХ = P + Q∙R,
значения компонентов которой приведены в таблицах 17.1 и 17.2, требуется выполнить:
1) на основании аналитической формы переключательной функции составить схему из графических обозначений элементов цифровой техники;
2) минимизировать переключательную функцию методом Вейча-Квайна;
3) проверить по таблице истинности тождество исходной и минимизированной переключательных функций;
4) для минимизированной переключательной функции составить принципиальную электрическую схему в релейно-контактном исполнении;
5) представить минимизированную переключательную функцию в текстовой форме, используя ключевые слова логических отношений: "если ... , то ...", "и", "или", "не" и наименования реальных элементов системы торможения.
Таблица 17.1
| Цифры варианта | Предпоследняя цифра кода варианта | |
| Р | Q | |
 a + b∙c∙d a + b∙c∙d
| a∙b∙c + d | |
| a + b∙c∙d | a + b∙c∙d | |
| a∙b + c∙d | a + b∙c∙d | |
| a∙b + c∙d | a + b∙c∙d | |
| a∙b∙c + d | a∙b + c∙d | |
| a∙b∙c + d | a∙b + c∙d | |
| a∙c + b∙d | a∙c + b∙d | |
| a∙c + b∙d | a∙c + b∙d | |
| a∙d + b∙c | a + b∙c∙d | |
| a∙d + b∙c | a + b∙c∙d |
Таблица 17.2
| Цифры варианта | Последняя цифра кода варианта |
| R | |
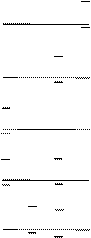 a + b + c + d a + b + c + d
| |
| a + b + c + d | |
| a + b + c + d | |
| a + b + c + d | |
| a + b + c + d | |
| a + b + c + d | |
| a + b + c + d | |
| a + b + c + d | |
| a + b + c + d | |
| a + b + c + d |
ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ И МАШИНЫ
Пример № 9.1
Магнитопровод трансформатора (рис. п9.1.1) изготовлен из пластин (горячекатаная сталь 1511, толщина 0,35 мм). Размеры магнитопровода: а = 70 мм, b = 50 мм, h = 200 мм и с = 110 мм. Воздушный эквивалентный зазор каждого из четырех стыков шихтованного магнитопровода равен 0,05 мм. Коэффициент заполнения магнитопровода, определяемый лаковой изоляцией между пластинами, kЗ.С. = 0,92. Требуется определить массу магнитопровода, предельно допустимую передаваемую мощность при частоте 50 Гц и число витков вторичной обмотки при условии, что первичное напряжение равно 220 В, вторичное напряжение равно 36 В, число витков первичной обмотки равно 160.
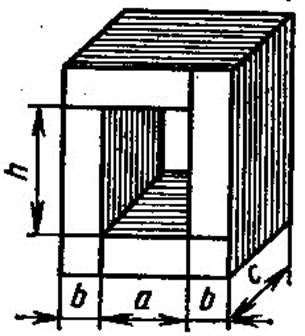
Рис. п9.1.1. Эскиз магнитопровода однофазного трансформатора
Решение
Расчет производим при допущении, что рассеяние магнитного потока отсутствует.
Сечение стали магнитопровода
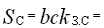
= 5·11·0,92 = 50,5 см2.
Длина средней линии сердечника
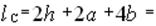
= 2·20 + 2·7 +4·5 = 74 см.
Масса сердечника
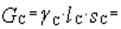
= 7,8·74·50,5 = 29148,6 г ≈ 30,15 кг.
Ориентировочное значение величины длительно передаваемой мощности определяем по формуле
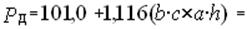
= 101 + 1,116·(5·11×7·20) = 8694,2 Вт ≈ 8,7 кВт.
Ориентировочное значение числа витков вторичной обмотки определяем по формуле
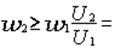
= 160 · 36/220 ≈ 26,18 ≈ 27 витков.0
Пример № 9.2
Для однофазного трансформатора (см. пример № 9.1) выполнить расчет напряженности магнитного поля в стальном сердечнике и воздушном зазоре магнитопровода, а также расчет мощности потерь в режиме холостого хода.
Решение
Расчет производим при допущении, что рассеяние магнитного потока отсутствует.
Магнитная индукция в магнитопроводе
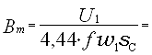
= 220/(4,44·50·160·50,5) ≈ 1,23 Тл.
По кривой намагничивания стали 1511 при переменном токе промышленной частоты (см. рис. п9.2.1) находим действующее значение напряженности магнитного поля в стали: Н~С = 3 А/см.
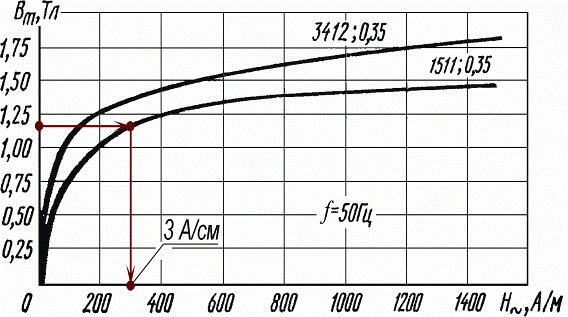
Рис. п9.2.1. Кривые намагничивания стали с примером ключа решения
Действующее значение напряженности магнитного поля в воздушном зазоре магнитопровода
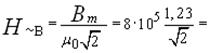
= 695793,073 ≈ 7·105 А/м = 7 кА/см.
Магнитодвижущая сила в режиме холостого хода определяется по закону полного тока
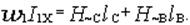
Длина средней линии сердечника
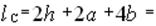
= 2·20 + 2·7 +4·5 = 74 см.
Длина четырех воздушных зазоров
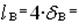
= 4·0,005 = 0,02 см.
Следовательно, м.д.с. составит
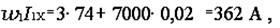
а ток холостого тока будет
I1X = w1I1X/w1 = 362/160 ≈ 2,3 A.
Для индукции 1,23 Тл удельные потери в стали по номограмме удельных потерь (см. рис. п9.2.2) составят 1,45 Вт/кг. Следовательно, для всего магнитопровода они будут около
РС = 1,45×30,15 ≈ 43,7 Вт.
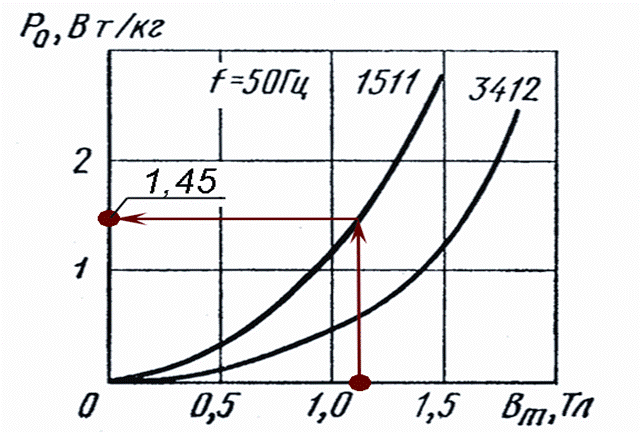
Рис. п9.2.2. Номограмма удельных потерь в стали
с примером ключа решения
Пример № 9.3
Для однофазного трансформатора (см. пример № 9.1) выполнить расчет активной и реактивной составляющих в режиме холостого хода, а также расчет сечения проводов обмоток трансформатора при длительно допустимой плотности тока 3 А/мм2 в номинальном режиме.
Решение
Активная составляющая тока холостого хода трансформатора
I1Х.А = РС/U1 = 43,7/220 = 0,199 ≈ 0,2 A.
Реактивная (намагничивающая) мощность сердечника (см. рис. п9.3.1) для индукции 1,23 Тл будет
QC = Q0GC = 15×30,15 ≈ 450 вар.
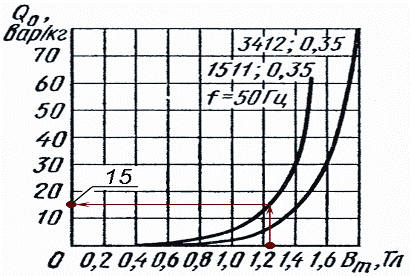
Рис. п9.3.1. Номограмма удельных реактивных потерь в стали
с примером ключа решения
Реактивная мощность, затрачиваемая на создание поля в воздушных зазорах сердечника равна
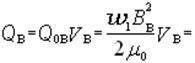
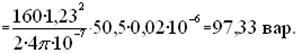
Реактивная составляющая тока холостого хода трансформатора будет
I1X.P = (QC + QB)/U1 = (450 + 97)/220 ≈ 2,5 A .
Ток холостого хода составит
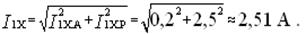
При передаваемой мощности в номинальном режиме 8,7 кВт ток во вторичной обмотке будет равняться приблизительно
I2НОМ ≈ РД/ U2 = 8700/36 ≈ 242 A .
При допустимой плотности тока в обмотке трансформатора 3 А/мм2, сечение провода вторичной обмотки должно быть не менее
sw2 ≥ I2НОМ/ 3 = 242/3 = 80,7 мм2.
Ток в первичной обмотке будет равняться приблизительно
I1НОМ ≈ РД/ U1 = 8700/220 ≈ 39,6 A .
Сечение провода первичной обмотки должно быть не менее
sw1 ≥ I1НОМ/ 3 = 39,6 /3 = 13,2 мм2.
Пример № 10.1
Найти номинальные токи I1НОМ, I2НОМ, ток холостого хода IК и сопротивления Z0, ZК Г-образной схемы замещения трехфазного трансформатора (см. рис. п10.1.1), технические данные которого приведены в таблице п10.1.1.
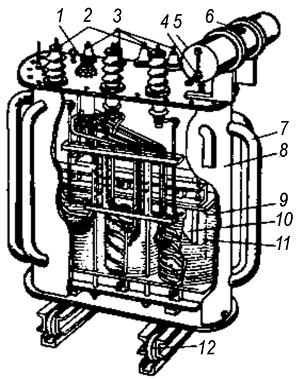
Рис. п10.1.1. Конструкция трехфазного трансформатора типа ТСМ
Таблица п10.1.1
Паспортные данные трансформатора ТСМ 60/35 (Y / Δ)
| Тип | SНОМ, кВА | U1 НОМ, кВ | U2 НОМ, В | iХ, % | uК, % | РX, Вт | РК.НОМ, Вт |
| ТСМ 60/35 | 11,1 | 4,55 |
Решение
В паспорте трехфазных трансформаторов указываются номинальная мощность и мощность потерь всех трех фаз. Под номинальными напряжениями понимаются линейные напряжения на зажимах трансформатора в режиме холостого хода, а под номинальными токами – линейные токи независимо от схемы соединения обмоток (звезда Y или треугольник Δ).
С учетом этого обстоятельства имеем.

 Номинальные токи
Номинальные токи
 I1 НОМ = S НОМ ⁄( 3 U1 НОМ) = 60000 ⁄ ( 3 35000) = 0,99 А,
I1 НОМ = S НОМ ⁄( 3 U1 НОМ) = 60000 ⁄ ( 3 35000) = 0,99 А,
 I2 НОМ = S НОМ ⁄( 3 U1 НОМ) = 60000 ⁄ ( 3 400) = 87,5 А.
I2 НОМ = S НОМ ⁄( 3 U1 НОМ) = 60000 ⁄ ( 3 400) = 87,5 А.
Ток холостого хода первичной обмотки
I Х = iXI1 НОМ = 0,11 · 0,99 = 0,1 A.
Схема замещения трехфазных трансформаторов составляется только для одной фазы, поэтому для ее расчета нужно использовать фазные напряжения, токи и мощности (мощность фазы равна 1/3 всей мощности трансформатора). У трансформатора ТСМ 60/35 первичные обмотки соединены звездой, а вторичные – треугольником, поэтому:
фазные напряжения будут
 U1 НОМ.Ф = U1 НОМ ⁄ 3 = 35 ⁄ 3 = 20,2 кВ,
U1 НОМ.Ф = U1 НОМ ⁄ 3 = 35 ⁄ 3 = 20,2 кВ,
U2 НОМ.Ф = U2 НОМ = 400 В,
фазные токи –
 I1 НОМ.Ф = I1 НОМ = 0,99 A,
I1 НОМ.Ф = I1 НОМ = 0,99 A,
I2 НОМ.Ф = I2 НОМ ⁄ 3 = 87,5 ⁄ 3 = 50,5 A,
активные сопротивления Г-образной схемы замещения –
R К = PК.НОМ ⁄(3I21 НОМ.Ф) = 1208 ⁄3·0,992 = 410,8 Ом,
R 0 = PX⁄(3I2X) = 502⁄3·0,12 = 16733,3 Ом,
полные сопротивления Г-образной схемы замещения –
Z К = uKU21НОМ.Ф ⁄SНОМ = 0,0455·350002⁄60000 = 928 Ом,
Z 0 = U1НОМ.Ф ⁄IХ = 20200 ⁄0,1 = 202000 Ом,
реактивные сопротивления Г-образной схемы замещения –

 XК = Z2К - R2К = 831 Ом,
XК = Z2К - R2К = 831 Ом,
X0 = Z20 - R20 = 201000 Ом .
Свернутая и подробная схемы замещения трансформатора приведены на рисунке п10.1.2.
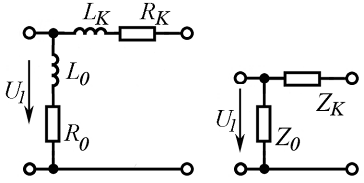
Рис. п10.1.2. Подробная и свернутая схемы замещения трансформатора
Пример № 10.2
Для трехфазного трансформатора ТМ-160/6 (см. табл. 10.2) с масляным охлаждением найти коэффициент нагрузки βmax, соответствующий максимальному к.п.д. ηmax при cosφП = 0,8.
Решение
Максимальный коэффициент нагрузки
 βmax = РX ⁄ РК.НОМ = 700 ⁄2000 = 0,59.
βmax = РX ⁄ РК.НОМ = 700 ⁄2000 = 0,59.
Максимальное значение к.п.д. при cosφП = 0,8 составит
ηmax = βmaxSНОМcosφП ⁄(βmaxSНОМ cosφП + β2maxPK.НОМ + PX) =
= 0,59·160000·0,8/(0,59·160000·0,8 + 0,592·2000 + 700) = 0,982.
Пример № 11.1
Для трехфазного асинхронного двигателя (ТАД) с короткозамкнутой обмоткой ротора типа 4А80Ф2У3 определить номинальную скорость вращения nном и число пар полюсов р на одну фазу двигателя
Решение
Из таблицы 11.1 известно, что синхронная скорость (скорость вращения магнитного поля статора) для ТАД типа 4А80A2У3 равна n0 = 3000 об/мин, а номинальное скольжение sНОМ = 5 %.
Номинальная скорость вращения ротора составит
nНОМ = n0·(1 – sНОМ ) =3000·(1- 0,05) = 2850 об/мин.
Число пар полюсов р на одну фазу обмотки статора составит
p = 60 · f ∕ n0 = 60 · 50∕3000 = 1,
то есть, ТАД типа 4А80Ф2У3 является двухполюсной машиной.
Пример № 11.2
Для ТАД типа 4А100L8У3 определить активную мощность Р1 статорной обмотки, вращающий момент МНОМ и построить механическую характеристику.
Решение
Из таблицы 11.1 известно, что для ТАД типа 4А100L8У3 (синхронная скорость n0 = 750 об/мин и номинальное скольжение sНОМ = 7 %) номинальная мощность на валу двигателя равна
РНОМ = 1,5 кВт = 1500 Вт.
Номинальный к.п.д. двигателя
ηНОМ = 74 % = 0,74.
Следовательно, активная мощность статорной обмотки составит
Р1 = РНОМ ∕ ηНОМ = 1,5 ∕ 0,74 ≈ 2 кВт = 2000 Вт,
а вращающий момент на валу равен
МНОМ = 9,55∙РНОМ ∕ nНОМ = 9,55∙1500 ∕ (750∙0,93) ≈ 22,54 Н∙м,
где nНОМ = n0 (1– sНОМ).
Известно (табл. 6.1), что для асинхронного двигателя типа 4А100L8У3 ММАХ ∕МНОМ = 2,2·МПУСК ∕ МНОМ = 1,8; ММIN ∕ МНОМ = 1,4. А так как МНОМ = 22,54 Н∙м, то
ММАХ = 2,2∙22,54 = 49,588 Н∙м,
МПУСК =1,8∙22,54 = 40,32 Н∙м,
ММIN = 1,4∙22,54 = 31,556 Н∙м.
Для расчета критической частоты вращения ротора используем формулу Клосса
MНОМ = 2MMAX ∕ (sНОМ ∕ sКР + sКР ∕ sНОМ).
Разрешив уравнение это уравнение относительно sКР, имеем:
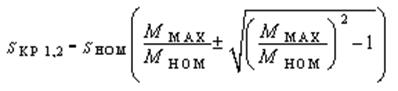
Поскольку sКР всегда больше sНОМ, следует найти только одно значение sКР:
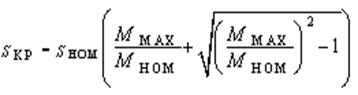 .
.
 Получим
Получим
SKP = 0, 03 · (2, 2 + (2, 2)2 – 1 ) = 0,125 .
При этом
nКР = n0·(1 – sКР ) =750·(1- 0,125) = 656 об/мин.
С учетом того, что при n0 = 750 об/мин момент равен нулю (холостой ход), а при МПУСК - n = 0, строим приближенный график (рис. п11.1) механической характеристики двигателя.
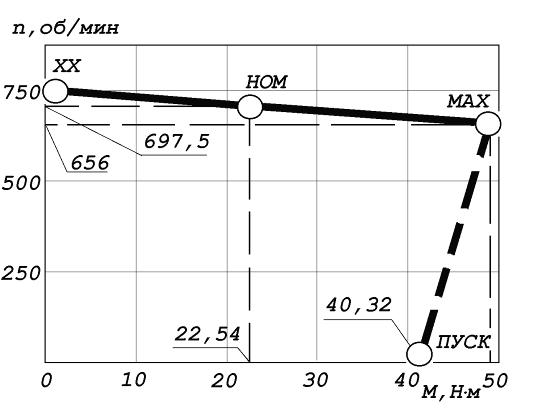
Рис. п11.2.1. Механическая характеристика ТАД 4А100L8У3
Пример № 11.3
Вычислить для ТАД из предыдущего примера потребляемую по одной фазе активную и полную мощность, а также рассчитать значение емкости СК батареи компенсационных конденсаторов для одной фазы при заданном значения коэффициента мощности λЗАД = 0,89.
Решение
Из каталожных данных (табл. 11.1) известно, что для ТАД типа 4А100L8У3 в номинальном режиме мощность на валу РНОМ равна 1,5 кВт при к.п.д. ηНОМ равном 74 % и с коэффициентом мощности λНОМ = cosφНОМ = 0,65. Следовательно, по одной фазе потребляется:
активной мощности
РФ = РНОМ ∕ 3 ηНОМ = 1500 ∕ 3·0,74 = 675,7 Вт;
полной мощности
SФ = РФ ∕ λНОМ = 675,7 ∕ 0,65 = 1040 ВА;
реактивной мощности
 QФ = PФ (1⁄λНОМ)2- 1 = 675,7 (1⁄0,65)2- 1 = 790 вар.
QФ = PФ (1⁄λНОМ)2- 1 = 675,7 (1⁄0,65)2- 1 = 790 вар.
Для обеспечения заданного коэффициента мощности λЗАД = 0,89 потребляемая реактивная мощность должна быть
 QФ.ЗАД = PФ (1⁄λЗАД)2 – 1 = 675,7 (1⁄0,89)2– 1 = 346,2 вар.
QФ.ЗАД = PФ (1⁄λЗАД)2 – 1 = 675,7 (1⁄0,89)2– 1 = 346,2 вар.
То есть, надо компенсировать конденсаторами
QК = QФ - QФ.ЗАД = 790 - 346,2 = 443,8 вар.
Величина емкости компенсирующего конденсатора
CК = QК ⁄2πfU2Ф = 443,8 ⁄2π50·2202 ≈ 0,000029 Ф = 29 мкФ.
Пример № 11.4
Для ТАД (cosφНОМ = 0,8; РНОМ = 1,5 кВт), включенного в сеть 220/380 В и имеющего нагрузочную диаграмму (см. рис. п11.4.1), определить среднеквадратичное (эквивалентное) значение мощности, среднеквадратичное (эквивалентное) значение тока и показатель ПВ относительной продолжительности включения.
Решение
Из анализа нагрузочной диаграммы ТАД (см. рис п11.2) следует, что:
Р1 = 1100 Вт, t1 = 1 мин;
Р2 = 1400 Вт, t2 = 3 мин;
Р3 = 1900 Вт, t3 = 1 мин;
Р4 = 1600 Вт, t4 = 1 мин;
Р5 = 700 Вт, t5 = 2 мин;
t0 = 3 мин; tЦ = 11 мин.
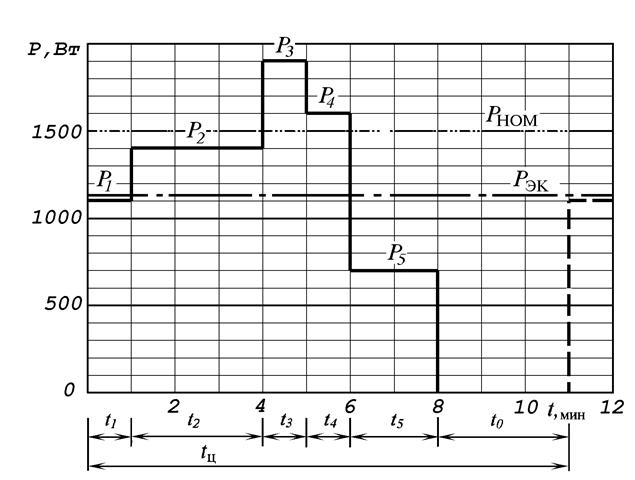
Рис. п11.4.1. Нагрузочная диаграмма работы ТАД
Среднеквадратичное (эквивалентное) значение мощности, потребляемой двигателем:
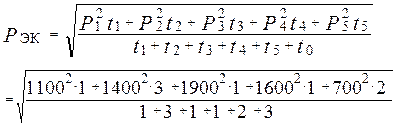
=
= 1137,8 Вт.
Дата добавления: 2016-03-20; просмотров: 1297;
