Обратимые реакции первого порядка
До сих пор мы говорили о необратимых реакциях. А если реакция обратима:
 |
Как в этом случае меняются концентрации веществ?
1. Рассматривая данную ситуацию, будем для определенности считать, что в начальный момент времени в системе присутствует только вещество А (в концентрации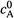 
).
а) Для прямой и для обратной реакций записываем уравнения скорости:
v+ = k+cA ; v– = k–cP = k–(c0A – cA) .(17.12,а-б)
Здесь учтено, что прирост концентрации продукта Р равен убыли концентрации вещества А.
б) Результирующее изменение концентрации вещества А – это разность двух скоростей: убыли Ав прямой реакции и образования в обратной реакции:
– dcA /dt = v+ – v– = k+cA– k–(c0A – cA) = (17.13,а-б)
 |
= – k– c0A+ (k+ +k– )∙cA ≡ a + b∙cA , (17.13,в-г)
a b
 |
или
Таково дифференциальное уравнение для рассматриваемой реакции. Оно приведено к виду, удобному для интегрирования.
в) I. Уравнения данного типа решаются путем замены:
 |
 |
и вместо (17.13, д) имеем:
II. Таким образом, для переменной zдифференциальное уравнение совпадает с уравнением (17.5); поэтому и решение его подобно формуле (17.9,б):
 |
 |
III. После подстановки z получаем явную зависимость концентрации вещества Аот времени; вначале — в такой форме:
 |
затем, с учетом вида а и b, — в окончательном виде:
 |
2. а) Здесь уже, в отличие от необратимой реакции, при t→ ∞ концентрация вещества А стремится не к нулю, а к некоторой отличной от него величине:
При такой предельной концентрации скорости
прямой и обратной реакций выравниваются, и наступает динамическое равновесие (рис. 17.4).
Таким образом,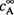 
— та самая равновесная концентрация вещества А, которая фигурирует, например, в константе равновесия реакции:
Теперь же выяснен закон, по которому происходит достижение этой концентрации.
б) Нетрудно определить и период полупревращения, исходя из условия:
 |
Подставляя это выражение в левую часть формулы (17.17), находим:
 |
Как и «полагается» реакции первого порядка, период полупревращения вновь
не зависит от концентрации, принимаемой за начальную.
Дата добавления: 2016-03-20; просмотров: 670;