Константа скорости и период полупревращения
1. Как следует из обобщенного дифференциального уравнения (16.9), скорость реакции зависит не только от концентрации реагентов, но и от фигурирующей в уравнении константы k, называемой константой скорости.
а) Очевидно, последняя равна скорости при единичных концентрациях реагентов.
б) Значение этой константы для каждой реакции своё и определяется природой реагирующих веществ, механизмом реакции и температурой. Таким образом, константа скорости является важнейшей характеристикой реакции. Именно
она определяет, будет ли идти реакция в заметных масштабах или нет, если
мы создадим обычные концентрации реагентов.
в) Размерность k легко определить, исходя из соответствующего дифференциального уравнения (см. табл. 16.3).
 |
Как видно, эта размерность зависит от порядка реакции.
 |
2. а) Кроме константы скорости, важной кинетической характеристикой реакции является период полупревращения,
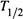. Это такое время, за котороеконцентрация какого-либо из реагентов снижается до среднего уровня между начальным и конечным значениями:
б) Так, пусть проходит необратимая реакция
 |
Ясно, что рано или поздно всё вещество А израсходуется, т.е.
 |
В данном случае период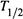 
— это время, за которое исходная концентрация уменьшается в 2 раза (рис. 16.1,а). Часто его называют периодомполураспада, что относится, например, и к реакциям радиоактивного распада ядер.
 |
в) А теперь пусть речь идет о реакции вида:
Когда реагент Вполностью израсходуется, останется избыток вещества А
(равный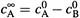 
).
Если скорость реакции оценивать по веществу А, то, очевидно, надо пользоваться общим определением (16.13), т.е. найти время, за которое концентрация вещества А достигает среднего уровня между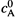 
и 
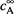(рис. 16.1,б).
3. Как практически находят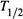 
?
а) Один способ: строят экспериментальную зависимость концентрации от
времени, т.е. кинетическую кривую (как на рис. 16.1,а-б). Если теперь поделить соответствующее расстояние по оси концентраций пополам, то можно найти искомое время.
 |
б) I. Второй способ: решить соответствующее дифференциальное уравнение,
т.е. получить интегральное уравнение, дающее зависимость концентрации от времени:
II. Для искомого момента 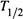это уравнение переписывается так:
 |
III. Решая его относительно времени, находим .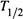
Краткое содержание главы 16
Этой главой мы начали новый раздел: «КИНЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ».
1. Определили, что под СКОРОСТЬЮ реакции чаще всего понимают скорость изменения молярной концентрации одного из участников реакции:
 |
2. Записали ОБОБЩЕННОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ СКОРОСТИ (принцип Гульдберга–Вааге) для реакций вида aA+bB→…:
 |
где в простейших случаях γa = a, γb = b. Уравнение дает зависимость скорости от концентрации реагентов.
3. Сказали также, что сумма Σγχ определяет ПОРЯДОК РЕАКЦИИ — нулевой, первый, второй, третий и т.д. Причем порядок часто совпадает с МОЛЕКУЛЯРНОСТЬЮ реакции, но все же — не всегда.
4. Наконец, кратко остановились на двух важнейших характеристиках реакций – КОНСТАНТЕ СКОРОСТИ k и ПЕРИОДЕ ПОЛУПРЕВРАЩЕНИЯ T½ .
Глава 17. ПРОСТЕЙШИЕ КИНЕТИЧЕСКИЕ
УРАВНЕНИЯ
В этой главе будет рассмотрена кинетика простых реакций разного порядка. При этом всякий раз будем придерживаться такого плана:
а) общее химическое уравнение,
б) дифференциальное уравнение скорости,
в) интегральное уравнение — линейная и явная формы, а также их графическое выражение,
г) период полупревращения.
Дата добавления: 2016-03-20; просмотров: 1172;