Возмущающему воздействию

По полученным кривым переходных процессов (рис.8.26 и рис.8.27) могут быть получены основные статические и динамические показатели статических САР при управляющем и возмущающем воздействиях:

а) по управляющему воздействию

,

,

;

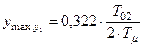б) по возмущающему воздействию

,

,

.

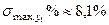Рассматриваемая система статическая по возмущению. В установившемся режиме обязательно 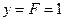или 0. Тот же сигнал на входе внутреннего контура, то есть на входе регулятора должен быть сигнал

.

8.10. Оптимизация САР по симметричному оптимуму

Как было показано ранее, любой оптимизированный по «модульному» оптимуму контур регулирования может быть представлен колебательным звеном с передаточной функцией

,

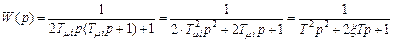где 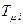- наименьшая постоянная времени рассматриваемого контура.

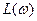с коэффициентом демпфирования . В этом случае логарифмическая амплитудная частотная характеристика имеет вид кривой 1-1 на рис.8.28. Важнейшим достоинством таких систем является возможность получения оптимального переходного процесса с минимальными значениями перерегулирования и времени регулирования. Кроме того, такой метод оптимизации обеспечивает простоту построения и расчета таких оптимальных систем. Однако, недостатком такого метода является то, что система регулирования в этом случае будет статической, поэтому в ряде случаев требования к точности регулирования не могут быть удовлетворены.

Из способа оптимизации по техническому оптимуму следует, что с целью придания оптимизированному контуру регулирования астатической характеристики в него вводится интегрирующее звено (если в объекте регулирования оно отсутствует). Обычно в рассматриваемых САР кроме управляющего воздействия имеется и возмущающее воздействие. В этом случае статическая ошибка регулирования при возмущающем воздействии может превысить допустимую величину. Для уменьшения либо исключения ошибки в этом случае необходимо изменить настройку системы регулирования. Рассмотренная ранее система является астатической по управляющему воздействию и статической по возмущающему воздействию. Это значит, что при приложении возмущения возникает статическая ошибка, величина которой пропорциональна этому возмущению.

Для получения системы астатической и по возмущающему воздействию необходимо иметь два интегрирующих звена.

Но система, имеющая 2 интегрирующих звена, является структурно неустойчивой, так как ее ЛАЧХ пересекает ось частот с наклоном -40 дб/дек. Для обеспечения устойчивости контура регулирования с двукратным интегрированием его ЛАЧХ (рис.8.28) кривая (2-2) должна повторять в зоне частоты среза наклон ЛАЧХ, равный –20 дб/дек.

Следовательно, ЛАЧХ двукратноинтегрирующей системы в области частоты среза должна иметь наклон -20 дб/дек. А переход к двукратному интегрированию, то есть переход в наклон -40 дб/дек должен осуществляться левее частоты среза (на октаву), т.е. при 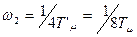, что симметрично по отношению к существующему перелому ЛАЧХ справа на одну октаву от частоты среза, т.е. . В связи с этим такой способ оптимизации с двухкратным интегрированием называется «симметричным оптимумом» по виду желаемой ЛАЧХ.

Передаточная функция разомкнутого контура регулирования, соответствующая ЛАЧХ, имеет вид

, (8.64)

Увеличение наклона низкочастотной части ЛАЧХ до –40дб/дек позволяет уменьшить динамические ошибки за счет увеличения коэффициента усиления в низкочастотной области ЛАЧХ. Логарифмическая фазовая частотная характеристика при этом также имеет симметричный характер относительно частоты среза . ЛФЧХ такой системы, рассчитанная по выражению представлена на рис.8.28. Из этой характеристики видно, что максимум запаса по фазе 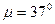будет иметь место примерно в середине среднечастотной амплитуды с наклоном – 20 дб/дек. Поэтому в теории автоматического управления они получили название симметричных.

Следовательно, система, настроенная по «симметричному оптимуму», будет астатической с астатизмом второго порядка (как по управляющему, так и возмущающему воздействиям). Для ЛАЧХ такой системы имеем следующие пропорции частот:

; ; ,

где ; ; ; .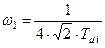

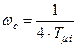Как было отмечено выше, астатическая САР должна быть двухкратноинтегрирующей. Внутренний контур САР, настроенный по модульному оптимуму, обеспечивает астатизм по управляющему воздействию. В связи с этим, при настройке САР по «симметричному» оптимуму внутренний контур должен быть настроен таким же образом, как и в однократноинтегрирующей системе, т.е. должен иметь оптимальную передаточную функцию.

В выражении (8.63) в качестве сомножителя входит выражение 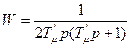, соответствующее разомкнутой оптимальной системе, настроенной по модульному оптимуму при аппроксимации внутреннего замкнутого контура. Передаточная функция разомкнутой системы, настроенной по симметричному оптимуму отличается от этого выражения множителем . Следовательно, для получения двухкратноинтегрирующей системы необходимо изменить передаточную функцию регулятора

, (8.65)

где - передаточная функция регулятора внешнего контура, настроенного по модульному оптимуму.

Передаточная функция замкнутой двухкратноинтегрирующей системы

. (8.66)