Параметры переходного процесса также оптимальны. Они получены при оптимальной настройке регулятора, при которой

,

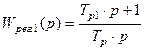где 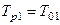- постоянная времени обратной связи регулятора;

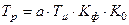- постоянная времени интегрирования регу-лятора;

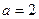- оптимальное значение коэффициента, определяющего соотношение постоянных времени замкнутого контура.

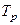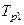На динамические показатели замкнутого внутреннего контура оказывает влияние действительная настройка регулятора, а именно, выбор значений постоянных времени регулятора и . Динамические показатели САР в этом случае могут быть оценены по частотным методам оценки качества САР. Для этого необходимо построить логарифмические амплитудную 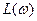и фазовую 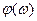частотные характеристики САР с использованием передаточных функций разомкнутой и замкнутой САР.

Наиболее точно динамические показатели могут быть определены путем расчета переходных процессов по методу структурного моделирования на ЦВМ. При этом желательно исследовать следующие варианты настройки параметров регулятора:

а) Изменение постоянной времени интегрирования 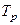регулятора:

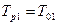
1) 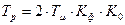- базовый вариант оптимальной настройки,

2)

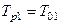
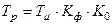
3)

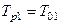
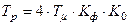
б) Изменение постоянной времени обратной связи 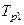регулятора:

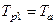
1) 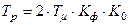- базовый вариант

4)

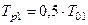
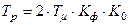
5)

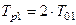
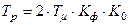
На рис.8.23 представлены в качестве примера переходные процессы внутреннего контура САР для рассмотренных выше вариантов:

а) при изменении 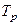; б) при изменении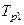

Анализ переходных процессов, представленных на рис.8.23, показывает:

- при уменьшении постоянной времени 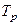(коэффициента 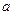) снижается время переходного процесса, но возрастает перерегулирование;

- при возрастании величины 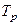(коэффициента 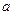) снижается перерегулирование за счет увеличения времени переходного процесса;

- изменение постоянной времени 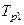в сторону уменьшения или увеличения по сравнению с оптимальным значением 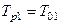приводит к увеличению перерегулирования при уменьшении времени переходного процесса в первом случае и увеличении его во втором случае;

- оптимальный переходный процесс обеспечивается только при оптимальной настройке регулятора, т.е. пр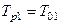и и 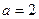(первый вариант).

По кривым переходных процессов или по их табличным данным могут быть определены показатели качества САР.

Для этой цели могут быть использованы также логарифмические амплитудная 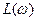и фазовая 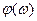частотные характеристики САР, построенные на основе передаточных функций разомкнутой и замкнутой системы для указанных вариантов изменения параметров регулятора. Например, передаточные функции разомкнутых САР при изменении 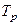(вариант 1,2 и 3) имеют вид

;

;

.

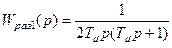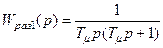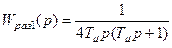Построенные для этих случаев ЛАЧХ 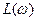и ЛФЧХ 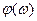представлены на рис.8.24.

Аналогично можно получить передаточные функции и построить логарифмические частотные характеристики системы при изменении постоянной времени .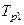

Пользуясь частотными методами можно определить запас системы по амплитуде и фазе, а также показатели качества САР.