Передаточные функции разомкнутой и замкнутой САР по управляющему воздействию

Рассмотрим передаточные функции внешнего замкнутого контура регулирования по управляющему воздействию для выходных координат внутреннего и внешнего контуров регулирования.

а) для выходной координаты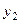

Передаточная функция внешнего разомкнутого и замкнутого контура для координаты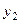

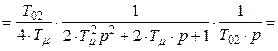
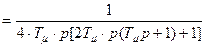, (8.49)

где 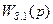- передаточная функция внутреннего замкнутого контура (8.47), т.е. этот контур является колебательным звеном.

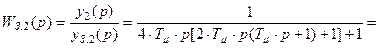
. (8.50)

Выражения (8.49) и (8.50) показывают, что внешний замкнутый контур по отношению к выходной координате имеет оптимальные передаточные функции системы третьего порядка (по управляющему воздействию).

Управление переходной функции для этой оптимальной системы запишется

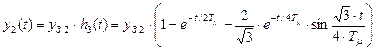. (8.51)

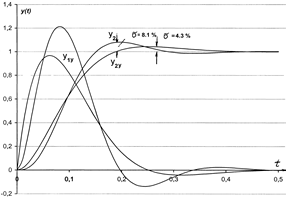
Кривая переходного процесса, построенная по этому выражению имеет вид (рис.8.26). В рассмотренном случае внутренний замкнутый контур представлен колебательным звеном с передаточной функцией (8.47).

Однако, учитывая, что 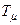является малой некомпенсируемой постоянной времени и 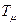<1 первым слагаемым в знаменателе передаточной функции можно пренебречь, т.к. 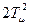<< 1.

В этой связи передаточная функция внутреннего замкнутого контура может быть представлена передаточной функцией апериодического звена первого порядка, т.е.

,

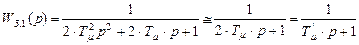где 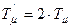- наименьшая некомпенсируемая постоянная времени внешнего контура.

Такая аппроксимация позволяет представить передаточную функцию внешнего замкнутого контура в виде

т.е. внешний замкнутый контур в этом случае представляется колебательным звеном (второго порядка).

Переходная функция внешнего контура в этом случае 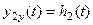рассчитывается по тому же выражению (8.23), что и для внутреннего контура и представлена на рис.8.26.

Следовательно, при аппроксимации (упрощенном) порядок системы снижается. При этом снижается перерегулирование =4,3 %.

б) для выходной координаты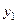

Передаточная функция по управляющему воздействию для выходной координаты внутреннего контура.

Передаточная функция имеет вид

или

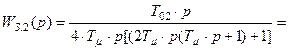
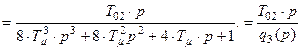. (8.52)

Аппроксимируя выражение

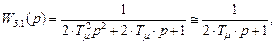
получим

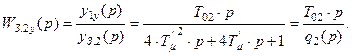(8.53)

Переходные характеристики могут быть найдены следующим образом. Из выражения (8.52) следует, что

.

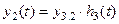В то же время .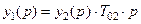

Отсюда можно записать

,

.

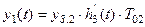Следовательно, выходная координата 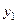является производной от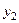

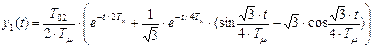. (8.54)

Для упрощенной САР, при аппроксимации внутреннего контура имеем

где

.

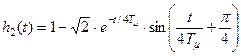Таким образом

. (8.55)

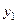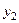Кривые переходных процессов при управляющем воздействии для и представлены на рис.8.26.

По рассчитанным кривым переходных процессов (по табличным данным), рассчитанным аналитически и на ЦВМ могут быть определены основные показатели качества регулирования статических САР 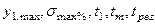и др. Для этого могут быть использованы такие логарифмические частотные характеристики, построенные для статической САР.

8.9.2. Реакция статической двухконтурной системы на возмущающее воздействие

1) Для выходной координаты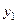

Передаточная функция разомкнутой системы

,

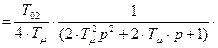
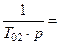
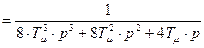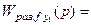
. (8.56)

Следовательно, при возмущающем воздействии реакция системы в отношении координаты 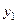будет такой же как при управляющем воздействии в отношении выходной координаты .

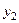Аналогично при аппроксимации внутреннего замкнутого контура передаточная функция разомкнутого и замкнутого контура будет

.

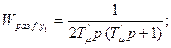
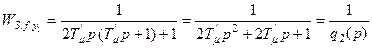Таким образом, переходная функция 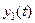при возмущающем воздействии может быть построена по следующим выражениям

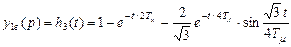, (8.57)

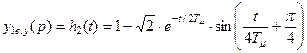. (8.58)

Кривые переходных процессов для 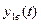представлены на рис.8.27.

2) Для выходной координаты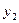

Передаточная функция разомкнутой системы

;

;

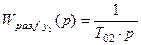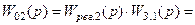
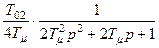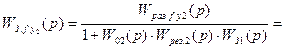
. (8.59)

В случае аппроксимации внутреннего замкнутого контура ( ) порядок уравнений снижается на один, поэтому

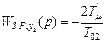
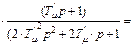
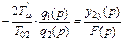, (8.60)

Отсюда

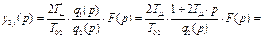
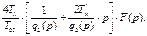
Поэтому для переходной функции выходной координаты при возмущающем воздействии можно записать

,

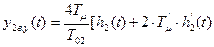где 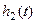- оптимальная переходная функция системы второго порядка;

.

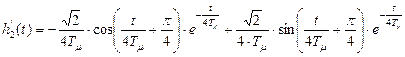Следовательно, для переходных функций можно записать следующие выражения

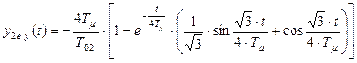. (8.61)

Учитывая то, что при единичном возмущающем воздействии 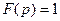на входе системы имеется задающее возмущение 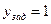, результирующая переходная функция для выходной координаты упрощенной аппроксимированной системы ПР4 возмущающему воздействии будет определяться следующим выражением

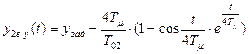. (8.62)

Аналогично путем подобных преобразований можно получить переходную функцию и для полной неапроксимированной системы

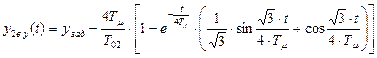. (8.63)

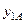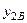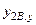На рис.8.27 представлены кривые переходных процессов статической САР по управляющему и возмущающему воздействиям для выходных координат и внутреннего, и внешнего контуров регулирования.

Рис.8.27 Кривые переходных процессов САР по