ПРИМЕРЫ РЕШЕНИЯ КОНТРОЛЬНЫХ ЗАДАНИЙ

8.1 Пример решения задачи по расчёту многоконтурной электрической цепи постоянного тока с помощью законов Кирхгофа

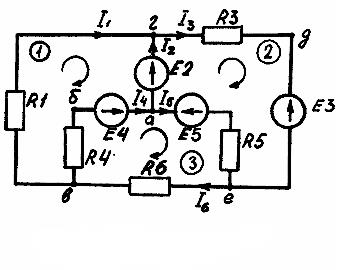
Используя схему :

- построить граф, определить число независимых уравнений, составленных на основе 1-го и 2-го законов Кирхгофа, выбрать системы независимых узлов и контуров схемы цепи;

-для независимых узлов и контуров схемы составить систему уравнений по законам Кирхгофа, записать ее в матричной форме. Определить значения всех элементов квадратной матрицы коэффициентов и матрицы-столбца свободных членов;

-решить полученную систему уравнений и определить значения токов всех ветвей рассматриваемой схемы цепи;

-проверить выполнение условия баланса мощностей;

-определить потенциалы точек, указанных на схеме. Построить потенциальную диаграмму для любого контура, содержащего не менее трех э.д.с.

Решение

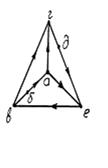
Для построения графа схемы изобразим вначале узлы а, в, г, е, а затем соединим их отрезками линий, заменяющих соответствующие ветви, как показано на рисунке 8.2. Укажем направление токов в ветвях графа.

При выборе независимых контуров наряду с построением графа необходимо построить и его дерево. Для этого соединим между собой узлы а, в, г, е так, чтобы не образовать ни одного контура как показано на рисунке 8.3а.

Для нахождения независимых контуров добавляем к полученному дереву по одной ветви (пунктирные линии на рисунках 8.3 б, в, г) так, чтобы каждый раз получался новый контур. Видим, что число независимых контуров равно трем (в-г-а-в; а-г-е-а; в-а-е-в).

Находим эти контуры на схеме и выбираем направления их обхода (указаны стрелками). Для найденных контуров записываем уравнения по второму закону Кирхгофа:

I₁R₁-I₄R₄=-E₂-E₄ (контур в-г-а-в),

I₃R₃-I₅R₅=E₂-E₃+E₅ (контур а-г-е-а),

I₄R₄+I₅R₅+I₆R₆=E₄-E₅ (контур в-а-е-в).

Найдем узловые уравнения. В качестве базисного узла выберем узел а. Тогда узлы в, г, е будут независимыми. Запишем для них уравнения по первому закону Кирхгофа:

-I₁-I₄+I₆=0,

I₁+I₂-I₃=0,

I₃+I₅-I₆=0.

-I₁-I₄+I₆=0,

I₁+I₂-I₃=0,

I₃+I₅-I₆=0,

I₁R₁-I₄R₄=-E₂-E₄,

I₃R₃-I₅R₅=E₂-E₃+E₅,

I₄R₄+I₅R₅+I₆R₆=E₄-E₅.

Чтобы записать полученную систему уравнений в матричной форме, подставим численные значения параметров и перепишем ее в виде:

-I₁+0×I₂+0×I₃-I₄+0×I₅+I₆=0,

I₁+I₂-I₃+0×I₄+0×I₅+0×I₆=0,

0×I₁+0×I₂+I₃-0×I₄+I₅-I₆=0,

22×I₁+0×I₂+0×I₃-20×I₄+0×I₅+0×I₆=-232,

0×I₁+0×I₂+14×I₃+0×I₄-16×I₅+0×I₆=112,

0×I₁+0×I₂+0×I₃+20×I₄+16×I₅+24×I₆=-4.

Запишем систему в матричной форме:

.

Решая полученную систему уравнений на ЭВМ с помощью программы “Решение систем линейных уравнений методом Гаусса" (автор Мальцев И.М.), получаем следующие значения токов:

I₁=-6,145A, I₂=9,182A, I₃=3,037 A,

I₄=4,84A, I₅=-4,342A, I₆=-1,305A.

Проверим правильность выполнения расчета, используя уравнения для узлов:

-I₁-I₄+I₆=-(-6,145)-4,84-1,305=0,

I₁+I₂-I₃=-6,145+9,182-3,037=0,

I₃+I₅-I₆=3,037-4,342-(-1,305)=0.

Первый закон Кирхгофа выполняется.

Проверим выполнение условия баланса мощностей:

,

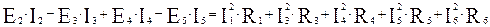120×9,182-124×3,037+112×4,84-116×(-4,342)=

=(-6,145)²×22+(3,037)²×14+(4,84)²×20+

+(-4,342)²×16+(-1,305)²×24 ,

1101,84-376,588-6,588+542,08+503,672=830,7425+129,12716+468,512+301,64742+40,8726 ,

1771 Вт»1770,902 Вт .

Баланс мощностей выполняется.

Для построения потенциальной диаграммы выбираем контур а-г-д-е-а c тремя э.д.с. Потенциал узла а выбираем равным нулю: j_a=0. Tогда потенциалы точек г, д, е контура будут равны:

j_г=j_a+E₂=0+120=120, В,

j_д=j_г-I₃×R₃=120-3,037×14=77,482 , В,

j_е=j_д-E₃=77,482-124=-46,518 , В,

j_a=j_e+E₅+I₅×R₅=-46,518+116-4,342×16=0.