Пример решения задачи на использование метода комплексных амплитуд и законов Кирхгофа в комплексной форме
Задача
Для схемы электрической цепи, изображенной на рисунке 8.5, с параметрами R1=1,8кОм, R2=3,3кОм, R3=1,2кОм, L1=3мГн, L3=0,6мГн, C1=680пФ, C3=480пФ, е1=24cos(106t - 690),B, е2=18cos(106t - 570),B :
-определить методом комплексных амплитуд текущие комплексы, действующие и мгновенные значения токов ветвей;
-найти комплексные действующие значения напряжений всех пассивных элементов цепи;
-построить векторные диаграммы токов и напряжений;
-проверить выполнение условия баланса мощностей;
-определить потенциалы точек, указанных на схеме, полагая jd=0.
Решение
Запишем систему уравнений по первому и второму законам Кирхгофа в комплексной форме:
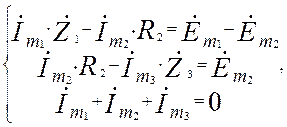
где
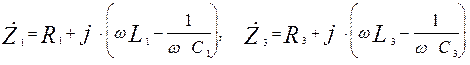 .
.
В матричной форме система уравнений будет иметь следующий вид:
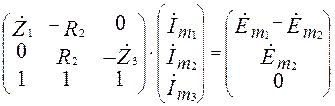 .
.
Определитель системы имеет вид:
 .
.
Для определения комплексных амплитуд токов 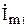 ,
, 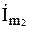 ,
,  найдем соответствующие определители D1, D2, D3:
найдем соответствующие определители D1, D2, D3:

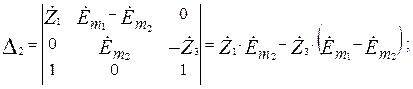
 .
.
Произведем вычисления:



Найдем определители D, D1, D2, D3:


Рассчитаем комплексные амплитуды токов:

Действующие значения токов будут равны:

Определим текущие комплексы i1(t), i2(t), i3(t):
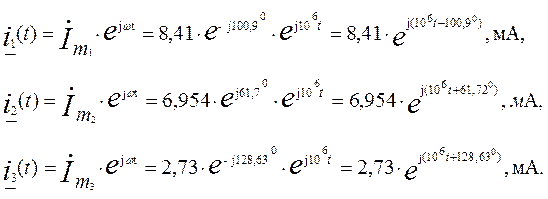
Рассчитаем комплексные действующие значения напряжений на всех пассивных элементах:

Для построения векторной диаграммы запишем уравнение Кирхгофа для узла 1 и выражения для напряжения 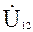 между узлами 1 и 2:
между узлами 1 и 2:
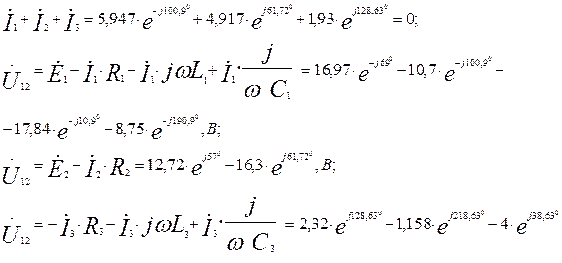
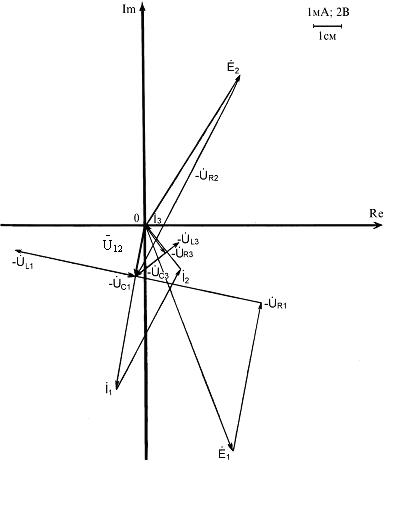
Выполняем построение векторных диаграмм в соответствии с рисунком 8.6.
Построение векторных диаграмм начнем с векторов токов. Выбираем масштаб: в 1см-1мА. Под углом -100,90 к действительной оси откладываем вектор I1 длиной 5,95см, из его конца под углом 61,70 к действительной оси откладываем вектор I2 длиной 4,9см, а из конца последнего откладываем под углом 128,60 к действительной оси вектор I3. Получим треугольник, одна из вершин которого находится в начале координат, что свидетельствует о равенстве нулю алгебраической суммы токов в узле. Векторные диаграммы напряжений строим исходя из приведенных выражений для напряжения 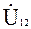 между узлами схемы. Выбираем масштаб: в 1см-2В. Построим вектор
между узлами схемы. Выбираем масштаб: в 1см-2В. Построим вектор 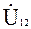 , используя первое из записанных равенств. Из начала координат под углом -690 к действительной оси откладываем вектор E1 длиной 8,5см. Из его конца - вектор
, используя первое из записанных равенств. Из начала координат под углом -690 к действительной оси откладываем вектор E1 длиной 8,5см. Из его конца - вектор  , длиной 5,35см, который будет параллелен вектору
, длиной 5,35см, который будет параллелен вектору 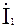 и противоположно ему направлен. Из конца последнего вектора перпендикулярно ему откладываем вектор
и противоположно ему направлен. Из конца последнего вектора перпендикулярно ему откладываем вектор  длиной 8,9см и направленный влево от вектора
длиной 8,9см и направленный влево от вектора  . И, наконец, из конца вектора
. И, наконец, из конца вектора  в противоположном ему направлении откладываем вектор
в противоположном ему направлении откладываем вектор 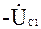 длиной 4,4см. Конец вектора
длиной 4,4см. Конец вектора 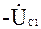 соединяем с началом координат и получаем вектор
соединяем с началом координат и получаем вектор 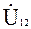 длиной приблизительно 1,8см, расположенный под углом -102,50 к действительной оси. Аналогичным образом строим вектор
длиной приблизительно 1,8см, расположенный под углом -102,50 к действительной оси. Аналогичным образом строим вектор 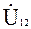 , используя сначала второе, а затем и третье выражения.
, используя сначала второе, а затем и третье выражения.

Проверяем выполнение условия баланса мощностей. Комплексная мощность источников 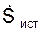 будет равна:
будет равна:
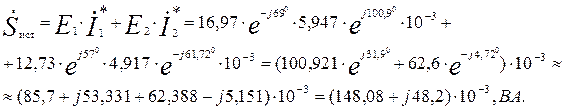
Комплексная мощность потребителей  имеет вид:
имеет вид:
 =Pп+jQп .
=Pп+jQп .
Найдем Pп и Qп:

Таким образом,
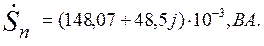
Сравнивая полученные результаты, видим, что 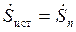 , т.е. баланс комплексных, а следовательно, и активных, и реактивных мощностей выполняется.
, т.е. баланс комплексных, а следовательно, и активных, и реактивных мощностей выполняется.
Найдем потенциалы указанных на схеме точек:

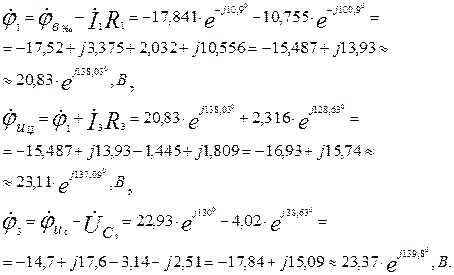
Дата добавления: 2016-03-20; просмотров: 3911;
