Основные формулы для определения скоростей и ускорений точек звеньев
Таблица 3.1
| № | Вид движения | Скорость | Ускорение |
Поступательное(ползун по стойке)
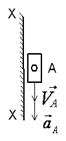
| Все точки звена имеют одинаковую скорость 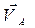 , вектор который направлен вдоль траектории движения точки A. , вектор который направлен вдоль траектории движения точки A.
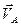 IIХ-Х IIХ-Х
| Все точки звена имеют одинаковые ускорения 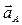 . Если вектор ускорения . Если вектор ускорения 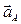 направлен в сторону направлен в сторону 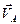 , то движение равноускоренное, если вектор ускорения , то движение равноускоренное, если вектор ускорения 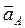 направлен в противоположнyю сторону направлен в противоположнyю сторону  , то движение равнозамедленное. , то движение равнозамедленное.
 II Х -Х II Х -Х
| |
Вращательное вокруг неподвижной оси
(кривошип или коромысло относительно стойки)
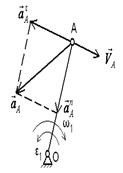
| Скорость точки А
 Вектор
Вектор 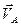 направлен перпендикулярно ОА, в сторону угловой скорости направлен перпендикулярно ОА, в сторону угловой скорости 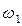 . .
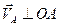
| Полное ускорение точки А
 Нормальное ускорение
Нормальное ускорение 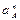 = = 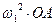 Вектор
Вектор 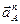 направлен по радиусу АО к центру вращения О. направлен по радиусу АО к центру вращения О.
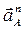 II OA.
Касательное ускорение II OA.
Касательное ускорение  Вектор
Вектор 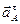 направлен перпендикулярно АО в сторону углового ускорения направлен перпендикулярно АО в сторону углового ускорения 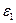

| |
Звено совершает плоскопараллельное движение
(шатун) 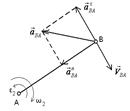
| Скорость точки В
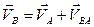 Относительная скорость
Относительная скорость
 Вектор
Вектор 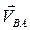 направлен перпендикулярно к ВА в сторону угловой скорости направлен перпендикулярно к ВА в сторону угловой скорости 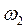 . .
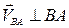
| Ускорение точки В
 Относительное ускорение
Относительное ускорение
 Нормальное ускорение
Нормальное ускорение
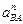 = = 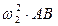 Вектор
Вектор 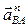 направлен параллельно АВ (от точки В к точке А) направлен параллельно АВ (от точки В к точке А)
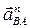 II ВА
Касательное ускорение II ВА
Касательное ускорение
 Вектор
Вектор  направлен перпендикулярно АВ направлен перпендикулярно АВ
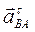 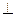 ВА ВА
|
Пример 3.1
Кинематический расчёт кривошипно-ползунного механизма. Определение скоростей точек звеньев для заданного положения механизма.
Дано:
1.Угловая скорость кривошипа является постоянной и равна  .
.
2.Размеры звеньев:
ОА = 20мм, АВ = 76мм, АС = 26мм.

План скоростей 
1. Определение скорости точки А.
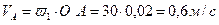 .
.
Вектор скорости 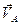 перпендикулярен кривошипу ОА.
перпендикулярен кривошипу ОА.
Выбираем масштаб плана скоростей 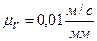 .
.
Найдём отрезок, изображающий вектор скорости 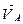 на плане:
на плане:
 .
.
Из полюса плана скоростей 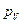 откладываем данный отрезок в направлении, перпендикулярном ОА в направлении угловой скорости
откладываем данный отрезок в направлении, перпендикулярном ОА в направлении угловой скорости 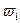 .
.
2. Определение скорости точки В.
Запишем векторное уравнение:
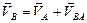 . Уравнение решаем графически.
. Уравнение решаем графически.
Направления векторов скоростей: 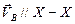 ,
,  .
.
Продолжим строить план скоростей, используя правило сложения векторов.
Из конца вектора 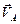 (точка
(точка 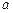 ) проводим направление вектора
) проводим направление вектора 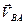 . Из полюса (точка
. Из полюса (точка 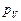 ) проводим направление вектора
) проводим направление вектора 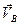 . На пересечении двух проведённых направлений получим точку
. На пересечении двух проведённых направлений получим точку 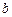 . Измеряя длины полученных отрезков и умножая их на масштаб
. Измеряя длины полученных отрезков и умножая их на масштаб  , получим значения скоростей:
, получим значения скоростей:


3. Определение скорости точки С.
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
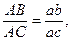
 мм
мм
Данный отрезок откладываем на продолжении отрезка 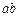 от точки а. Точку
от точки а. Точку 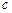 соединяем с полюсом
соединяем с полюсом 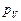 .
.
Величина скорости точки С:
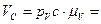

4. Определение угловой скорости шатуна АВ.
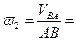 с-1
с-1
Для определения направления  переносим вектор
переносим вектор 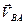 в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует
в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует  . В данном случае угловая скорость
. В данном случае угловая скорость  направлена против часовой стрелки.
направлена против часовой стрелки.
| Исследуемая величина | Отрезок на плане | Направление | Величина отрезка на плане, мм | Масштабный коэффициент μv | Значение величины, м/с |
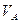
|  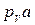
| 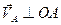 
|  
| ||
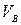
| 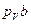
| 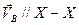
| |||

| 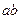
| 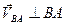
| |||

| 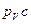
| ||||
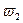
|
Пример 3.2
Кинематический расчёт кривошипно-ползунного механизма. Определение ускорений точек звеньев для заданного положения механизма.
Дано:
1.Угловая скорость кривошипа является постоянной и равна 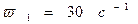 ,
, 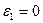 .
.
2.Размеры звеньев: ОА = 20мм, АВ = 76мм, АС = 26мм, AS2 = 25 мм.
Решение:
1.Определение ускорения точки А.
Так как угловая скорость 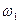 является постоянной, то
является постоянной, то 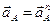 .
.
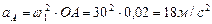 .
.
Вектор ускорения 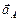 направлен параллельно кривошипу ОА от точки А к точке О.
направлен параллельно кривошипу ОА от точки А к точке О.
Выбираем масштаб плана ускорений 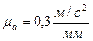 . Найдём отрезок, изображающий вектор ускорения
. Найдём отрезок, изображающий вектор ускорения 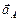 на плане:
на плане: 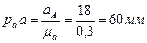 . Из полюса плана ускорений
. Из полюса плана ускорений  откладываем данный отрезок в направлении, параллельном АО.
откладываем данный отрезок в направлении, параллельном АО.

План ускорений 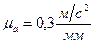
2.Определение ускорения точки В.
Запишем векторное уравнение: 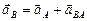 . Уравнение решаем графически.
. Уравнение решаем графически.
Вектор относительного ускорения  раскладываем на нормальную и касательную составляющие:
раскладываем на нормальную и касательную составляющие:  .
.
Нормальное относительное ускорение равно:
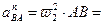
 .
.
Найдём отрезок, изображающий вектор ускорения  на плане:
на плане: 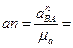

Продолжаем строить план ускорений, используя правило сложения векторов. Вектор ускорения  направлен параллельно АВ. Откладываем отрезок
направлен параллельно АВ. Откладываем отрезок 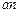 из точки
из точки 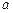 плана ускорений в указанном направлении от точки В к точке А.
плана ускорений в указанном направлении от точки В к точке А.
Вектор ускорения 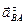 направлен перпендикулярно АВ. Проводим это направление из точки
направлен перпендикулярно АВ. Проводим это направление из точки 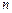 плана ускорений. Вектор ускорения
плана ускорений. Вектор ускорения 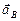 направлен параллельно оси x – x. Проводим это направление из полюса
направлен параллельно оси x – x. Проводим это направление из полюса  . Две прямые линии, проведённые из точек
. Две прямые линии, проведённые из точек 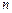 и
и  в указанных направлениях, пересекаются в точке
в указанных направлениях, пересекаются в точке 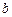 .
.
Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб 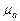 , получим:
, получим:

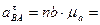
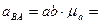
Дата добавления: 2016-03-20; просмотров: 914;
