Структурная схема механизма.
 |
2.Звенья механизма
| Звено ззвзвеназвена | Наименование | Подвижность | Число подвижных звеньев |
Кинематические пары
| № п/п | Обозначение на структурной схеме | Соединяемые звенья | Вид | Тип пары | Индекс пары | |
| Характер соприкосновения | Степень подвижности | |||||
Число одноподвижных кинематических пар p1=7, число двух подвижных кинематических пар р2=0.
Степень подвижности механизма
Строение групп Асcура
А).Последняя группа Асcура
Б).Предпоследняя группа Асcура
В).Начальный механизм
Структурная формула всего механизм
7.Класс всего механизма II, так как наивысший класс группы Ассура, входящей в данный механизм II.
ЛЕКЦИЯ 3
Краткое содержание
Определение скоростей и ускорений точек звеньев при поступательном, вращательном и плоскопараллельном движениях. Планы скоростей и ускорений. Принцип подобия в планах скоростейи ускорений. Примеры кинематического исследования механизмов.
Теоретические предпосылки определения скоростей и ускорений
Основные формулы для определения скоростей и ускорений точек звеньев механизмов приведены в таблице 3.1.
Планы скоростей и ускорений
Планом скоростей (ускорений) называется диаграмма, на которой от некоторого центра (полюса) в масштабе отложены векторы скоростей (ускорений) точек тела.
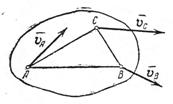
Рассмотрим тело, совершающее плоскопараллельное движение (рис.3.1).
Для плоскопараллельного движения скорости точек определяются по формулам:
 , ,
, ,  (3.1)
(3.1)
где  ,
, 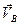 ,
,  - абсолютные скорости точек А, В, С;
- абсолютные скорости точек А, В, С;
 ,
,  - относительные скорости.
- относительные скорости.
Необходимо найти относительные скорости  ,
,  .
.
План скоростей получим, если в выбранном масштабе 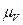 (
(  ) отложим от полюса
) отложим от полюса 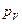 отрезки
отрезки 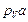 ,
,  и
и 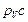 , параллельные векторам скоростей
, параллельные векторам скоростей 
 ,
, 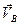 ,
,  . Отрезки находятся по формулам:
. Отрезки находятся по формулам:  ,
, 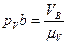 ,
, 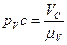 .
.
|
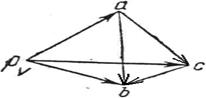
В результате построения плана скоростей получен треугольник авс (рис.3.2),который подобен треугольнику АВС. Найдем относительные скорости  и
и  по формулам:
по формулам:
|
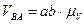 ,
, 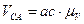 .
.
Рис.3.1 Рис.3.2
Сформулируем принцип подобия в плане скоростей:
В плане скоростей векторы относительных скоростей точек жесткого звена образуют фигуру, подобную звену, повернутую на угол 90° в сторону угловой скорости звена.
Следствие.
Пользуясь принципом подобия, достаточно на плане скоростей построить векторы скоростей только двух точек жесткого звена. Скорость же любой третьей точки определится путем построения фигуры или линии подобной данному звену.
Аналогично формулируется принцип подобия в плане ускорений.
Дата добавления: 2016-03-20; просмотров: 697;
