УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ.

Общие теоремы об устойчивости не позволяют даже в простейших случаях по коэффициентам уравнения без вычислений судить об устойчивости его решений. Получение таких коэффициентных условий даже для частных классов уравнений представляет большой интерес. В первую очередь изучаются линейные уравнения c постоянными коэффициентами.

1. Критерий Рауса - Гурвица. Рассмотрим систему линейных дифференциальных уравнений c постоянными коэффициентами

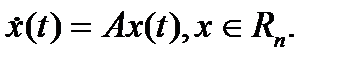(1)

Напомним некоторые сведения, касающиеся структуры общего решения уравнения (1).

Предположим сначала, что матрица 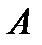имеет только простые, собственные значения 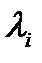и собственные векторы 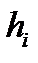, т. e.

Рис. 1. Жорданова форма матрицы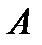

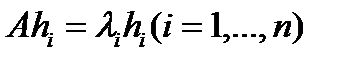. Тогда общее решение уравнения (1) имеет вид

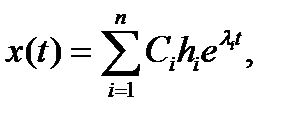
где 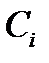- произвольные постоянные.

При наличии кратных собственных значений для построения общего решения уравнения (1) приведем сначала матрицу 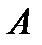к жордановой форме. Жордановой формой матрицы называется клеточно-диагональная форма, в которой главную диагональ образуют клетки Жордана, a все остальные элементы равны нулю.

При этом клеткой Жордана называется квадратная матрица, y которой на главной диагонали находится одно и то же число, элементы одного ряда выше главной диагонали равны единице, a все прочие элементы нулю (см. рис. 1, где изображены клетки Жордана, a все элементы вне диагональных блоков равны нулю).Возможны различные способы приведения матрицы квадратной матрицы 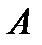размерности к жордановой форме. Приведем один из них, состоящий из следующих этапов:

1⁰. Для каждого находят наибольший общий делитель 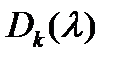всех миноров порядка 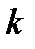характеристической матрицы 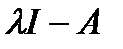. Старшие коэффициенты y всех полиномов 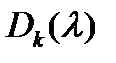берут равными единице. При этом

.

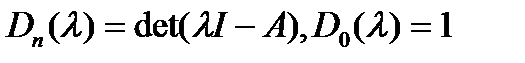2⁰. Находят инвариантные многочлены 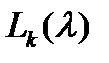(называемые так же инвариантными множителями) по формулам

.

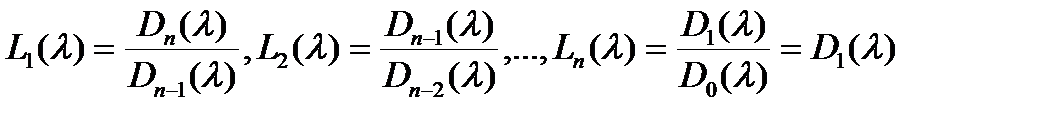3⁰. Каждый инвариантный многочлен раскладывают на различные неприводимые многочлены, называемые элементарными делителями характеристической матрицы 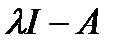или просто матрицы 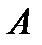. Элементарный делитель представляют в виде степени одной из разностей 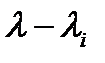, где 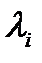— собственные значения матрицы 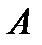. Таким образом, 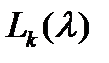имеет вид

.

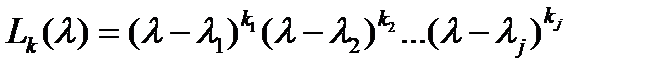Отметим, что произведение всех элементарных делителей равно произведению всех инвариантных множителей и равно .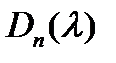

4⁰. Каждому элементарному делителю 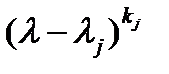сопоставляют клетку Жордана порядка 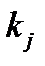с числом 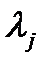на главной диагонали. Клеточно-диагональная матрица, y которой на главной диагонали находятся все построенные указанным образом клетки Жордана, и есть жорданова форма матрицы . Жорданова форма матрицы единственна с точностью до порядка расположения ее клеток Жордана на главной диагонали.

Приведем теперь формулы, определяющие общее решение уравнения (1) в случае кратных корней. Пусть 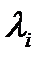‑ 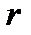-кратное собственное значение матрицы 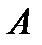. Ему соответствует некоторое количество собственных векторов. Степень вырождения собственного значения 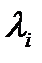равна максимальному числу 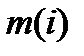линейно независимых собственных векторов, отвечающих 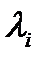. Число 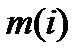равно также числу клеток Жордaна, соответствующих 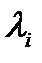. Обозначим через 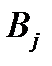одну из этих клеток. 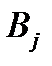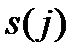Если размерность клетки Жордана есть , то

.

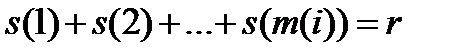Отсюда, в частности, видно, что жорданова форма матрицы 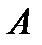является диагональной, если кратность любого ее собственного значения равна его степени вырождения. B этом случае все собственные значения имеют простые элементарные делители. Каждой клетке Жордaна 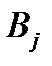соответствует серия векторов 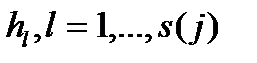(своих для каждой клетки), таких, что

.

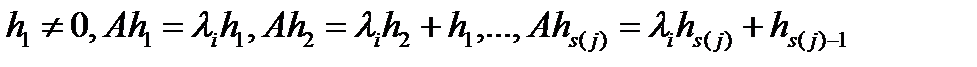Векторы 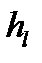, где 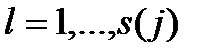, каждой серии линейно независимы между собой. Подпространство, натянутое на все векторы 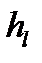, соответствующие клетке , является инвариантным, циклическим и имеет размерность, равную размерности серии, т. е: равную . В базисе, составленном из векторов всех серий, матрица 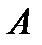имеет жорданову форму.

Вернемся к уравнению (1). Решениями этого уравнения являются функции вида

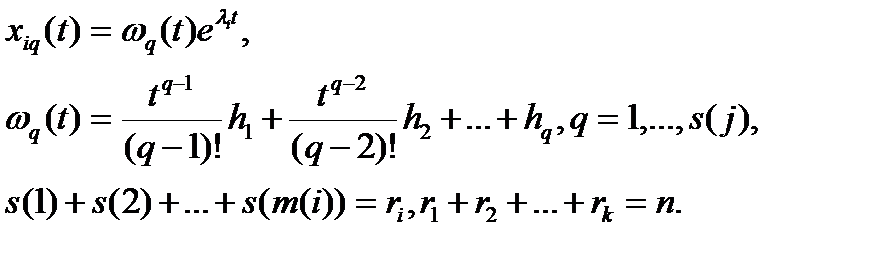(2)

Количество линейно независимых решений вида (2) равно 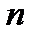. Общее решение уравнения (1) есть линейная комбинация из частных решений вида (2).

Из описанного представления общего решения линейной стационарной системы немедленно вытекает следующая теорема.

Теорема 1. Для устойчивости тривиального решения уравнения (1) необходимо и достаточно, чтобы все собственные значения 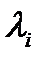матрицы 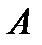удовлетворяли условию 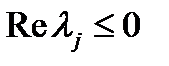, причем собственные значения 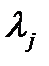такие, что 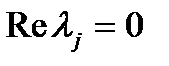, имеют простые элементарные делители (т. e. в формуле (2) все 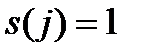). Для асимптотической устойчивости уравнения (1) необходимо и достаточно, чтобы .

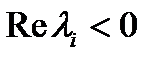Таким образом, устойчивость асимптотическая устойчивость или неустойчивость уравнения (1) определяется расположением относительно мнимой оси корней характеристического уравнения матрицы :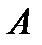

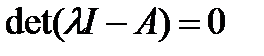. (3)

Здесь 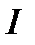— единичная ( 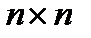)-матрица. Раскрывая определитель, можно привести уравнение (3) к виду

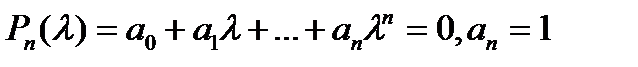. (4)

Будем говорить, что многочлен 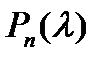является устойчивым многочленом (многочленом Гурвица), если все его корни 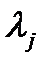имеют отрицательную вещественную часть, т. e.

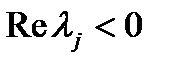. (5)

При выполнении условия (5) матрицу 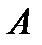также называют устойчивой.

Теорема 2 (А. Стодола). Все коэффициенты устойчивого многочлена положительны.

□ Пусть 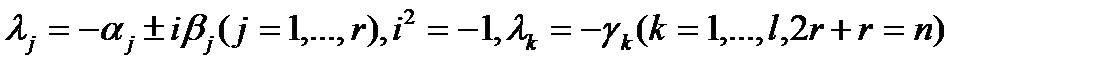— корни устойчивого многочлена 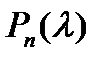. Тогда 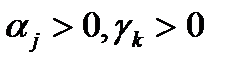и, раскладывая 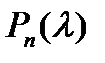на множители, имеем

.

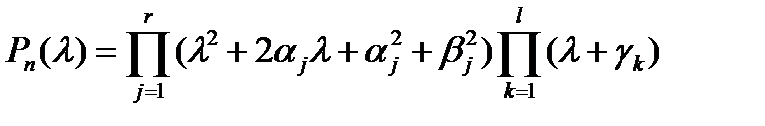Таким образом, 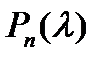представлен в виде произведения многочленов c положительными коэффициентами. Поэтому все его коэффициенты . ■

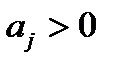Положительность коэффициентов есть необходимое, но не достаточное условие для выполнения неравенств (5). Например, многочлен 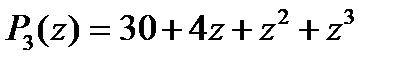имеет корни .

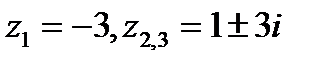Сформулируем теперь необходимый и достаточный признак устойчивости. Матрицей Гурвица 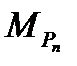многочлена (4) называется матрица вида

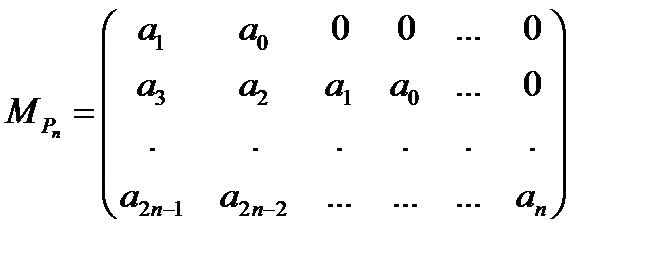. (6)

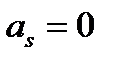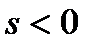В матрице (6) все при и . Например, для многочлена шестой степени матрица Гурвица такова:

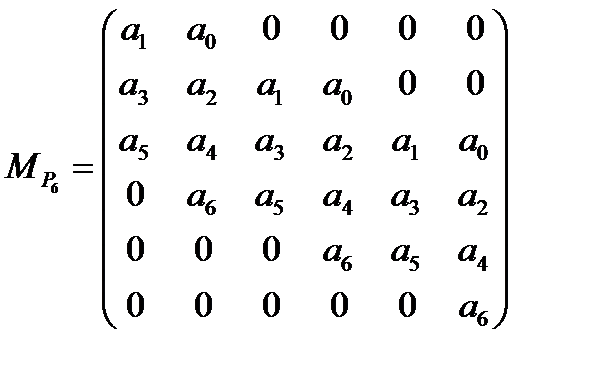(7)

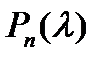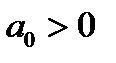Критерий Paуса — Гурвица. Для того чтобы многочлен c и 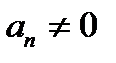был устойчивым, необходимо и достаточно, чтобы были положительны все главные диагональные миноры

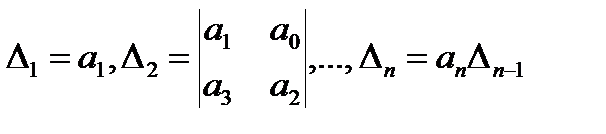
его матрицы Гурвица .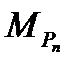

Критерий Льенара ‑ Шипара. Для того чтобы многочлен c положительными коэффициентами был устойчивым, необходимо и достаточно выполнение одного из двух условий: а) 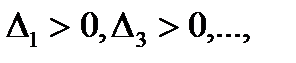, б) .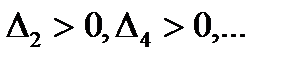

В качестве примера рассмотрим многочлен

.

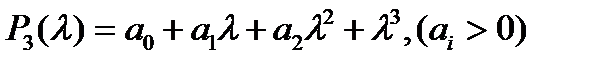Из вида матрицы (6), используя критерий Льенара ‑ Шипара, получим, что многочлен 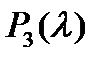является устойчивым, если .

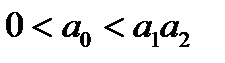2. Частотные критерии устойчивости. Применение критерия Рауса - Гурвица к реальным системам автоматического регулирования приводит к сложным вычислениям и не позволяет выявить влияние отдельных параметров на устойчивость системы. Более удобными в приложениях оказываются частотные критерии A. B. Михайлова и Г. Найквиста.

Рассмотрим многочлен (4). Положим 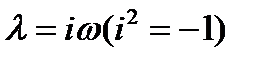и построим годограф Михайлова (амплитудно-фазовую характеристику) 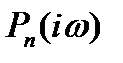этого многочлена:

.

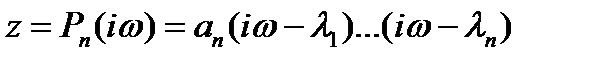Геометрически 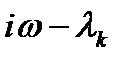есть вектор в комплексной плоскости 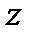, началом которого служит точка 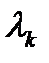— корень многочлена 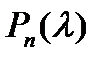, a концом - точка .

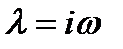Так как 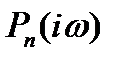— комплексное число, то

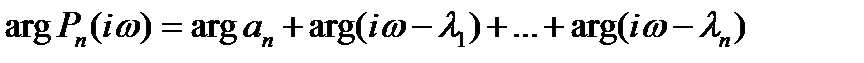. (8)

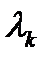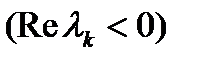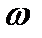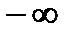Если корень лежит в левой полуплоскости , то при изменении от до 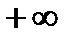вектор 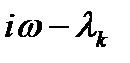вращается в положительном направлении (против хода часовой стрелки) и приращение аргумента равно :

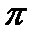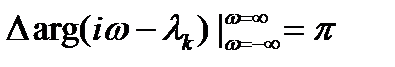. (9)

Если же корень 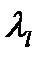лежит в правой полуплоскости, то вектор ( 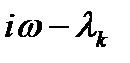) вращается по ходу часовой стрелки и

.

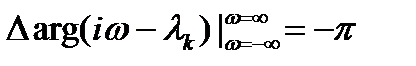Из соотношений (8) и (9) вытекает следующая теорема.

Теорема 3. Многочлен 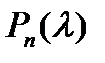, не имеющий чисто мнимых корней, является устойчивым тогда и только тогда, когда

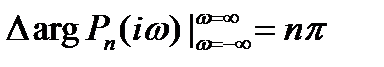(10)

Для упрощения условия (10) отделим действительную и мнимую части 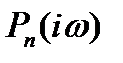. Имеем

.

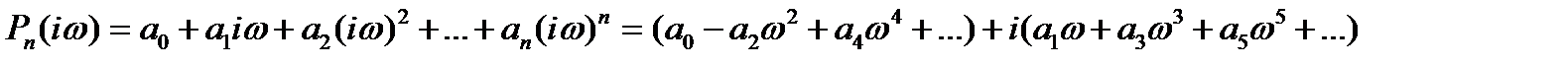Отсюда видно, что 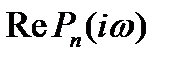есть четная функция от 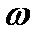, a 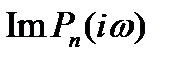- нечетная. Поэтому годограф многочлена 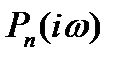состоит из двух частей, симметричных относительно действительной оси, первая из которых соответствует изменению 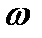от 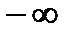до 0, a вторая — от 0 до 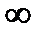. В результате получаем следующее утверждение.

Критерий Михайлова. Для устойчивости многочлена 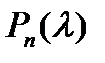, не имеющего чисто мнимых корней, необходимо и достаточно, чтобы

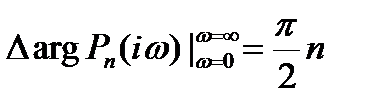. (11)

На рис. 2 приведены различные годографы Михайлова для 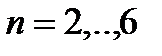. Чем ближе годограф подходит к началу координат, тем меньше запас устойчивости. Если годограф проходит через начало координат, то система находится на границе области устойчивости. Таким образом, критические значения параметров и частоты , линейной стационарной системы c характеристическим. уравнением (4) находят из условий

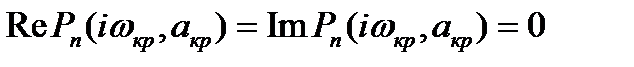
Чтобы подчеркнуть зависимость многочлена (4) от параметров 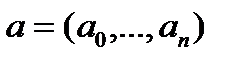, он обозначен через 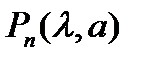. Интересно отметить, что на практике амплитудно-фазовую характеристику можно определить экспериментально, подавая на вход линейной стационарной системы сигнал частоты 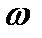и амплитуды 1. На выходе системы получится сигнал той же частоты 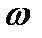, a амплитуда 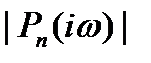окажется сдвинутой по фазе на 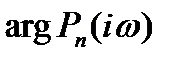относительно входного сигнала.

3. Система автоматической подстройки частоты гетеродинного приемника. B гетеродинных приемниках для обеспечения качественного звучания основное усиление производится на фиксированной, так называемой промежуточной частоте 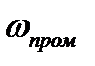Поскольку частота принимаемого сигнала 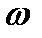постоянно меняется из-за разного рода неконтролируемых возмущений, для обеспечения хорошей работы гетеродинного приемника в его состав вводят систему автоматической подстройки частоты (АПЧ). Задачей системы АПЧ является поддержание заданного значения 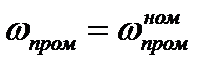. Одна из возможных систем АПЧ изображена на рис. 3.

Рис. 2. Годографы Михайлова для устойчивых систем при n=2,3,4,5,6

Рис. 3. Система автоматической подстройки частоты гетеродинного приемника: 1 — смеситель; 2 — усилитель промежуточной частоты; 3— дискриминатор; 4— усилитель; 5 – управляющий элемент гетеродина

Работа каждого из устройств 1-5 описывается следующими соотношениями, записанными сразу для отклонений частот :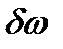

1. Смеситель: .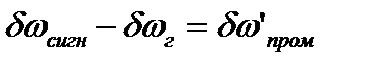

2. Усилитель промежуточной 'частоты (УПЧ):

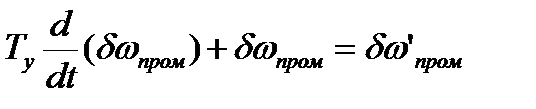
3. Дискриминатор: ,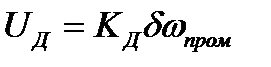

4. Усилитель: .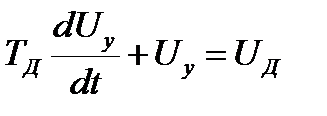

5. Управляющий элемент гетеродина:

.

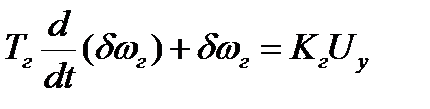Входной величиной .АПЧ будем считать 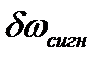, а выходом 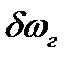, т, e, будем рассматривать АПЧ как следящую систему. Применяя операторный метод, получим:

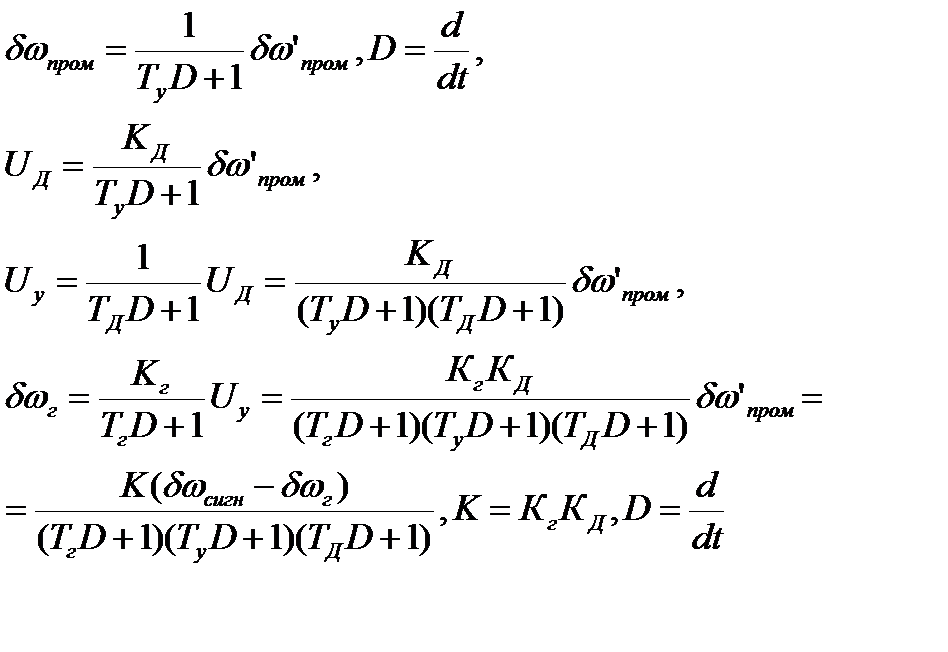
Окончательно получим уравнение АПЧ в виде

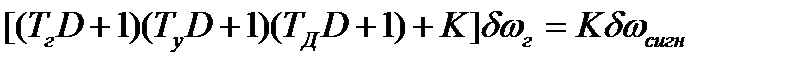(12)

Установим условия устойчивости АПЧ, описываемой уравнением (12), Воспользуемся критерием Михайлова, Построим годограф:

.

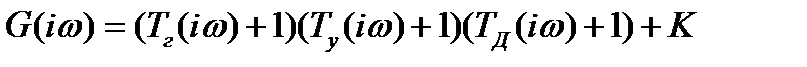Отделим действительную и мнимую части:

.

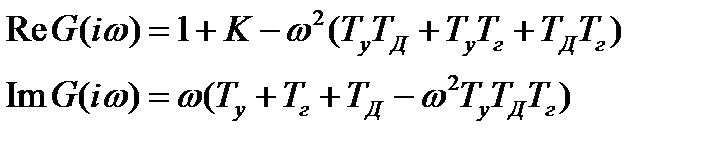Определим критический коэффициент усиления 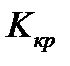и, критическую частоту 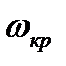из условий 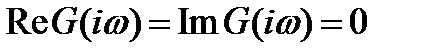. Из условия 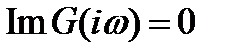находим, что

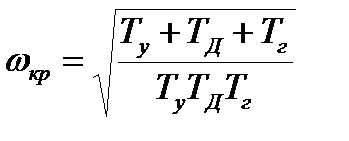
a из условии 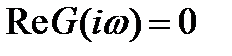— что

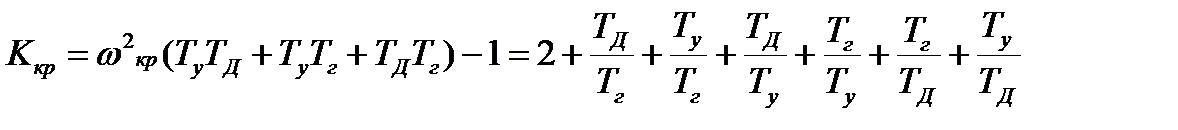
При значениях 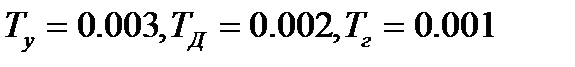получим 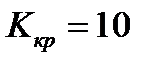. Следовательно, такая система АПЧ при 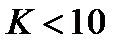устойчива, a при 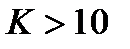- неустойчива.

4. Линейные одноконтурные системы автоматического регулирования. Вывод, аналогичный предыдущему, верен и для любой одноконтурной системы автоматического регулирования (САР), содержащей произвольное число звеньев (рис. 4). Пусть характеристическое уравнение одноконтурной системы имеет вид

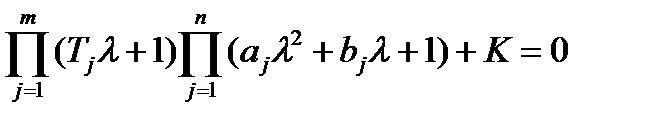(13)

Первые 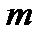сомножителей в (13) соответствуют апериодическим звеньям, вторые 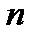— колебательным.

Рис. 4. Произвольная одноконтурная система автоматического регулирования

Теореме 4. Для любой одноконтурной САР c характеристической функцией (13) существует критическое значение коэффициента усиления 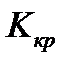такое, что при 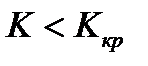система устойчива, a при 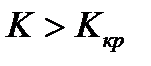она неустойчива.

5. Робастная устойчивость. Приведенные в теоремах этого параграфа условия устойчивости получены в предположении, что все коэффициенты системы 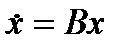, т. e. все элементы постоянной матрицы 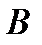, априори известны точно. Однако указанное предположение не всегда выполняется. В реальной ситуации зачастую бывает известна лишь некоторая область 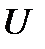, которой принадлежит матрица 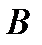. Ясно, что если устойчивость имеет место при любой матрице 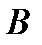из области 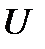, то реальная система также будет устойчива. Оказывается, что в некоторых ситуациях об устойчивости всех систем при произвольных матрицах 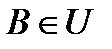можно судить по их отдельным представителям.

Приведем соответствующие утверждения.

Пусть 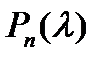— характеристический. многочлен матрицы 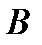, a 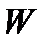- множество всех таких многочленов, соответствующих всем матрицам 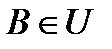. Произвольный многочлен 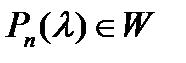запишем в виде

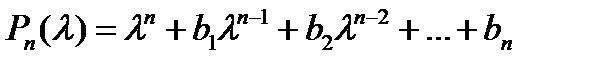(14)

Предположим, что известны границы изменения коэффициентов 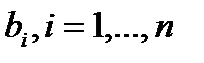, когда многочлен 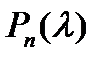пробегает множество 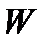. Иначе говоря, предположим, что известны числа 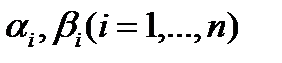такие, что

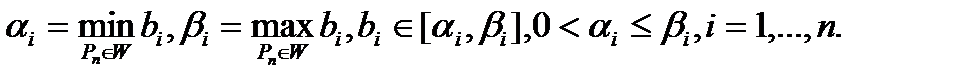(15)

Оказывается, что для проверки устойчивости всего бесконечного множества многочленов 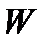достаточно убедиться в устойчивости только четырех многочленов: .

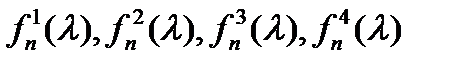Коэффициенты 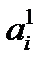многочлена 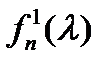таковы:

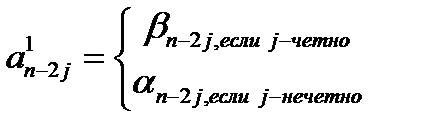
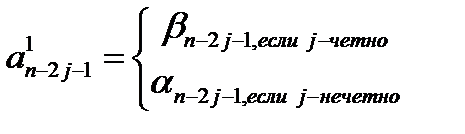
Коэффициенты многочлена 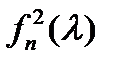имеют вид:

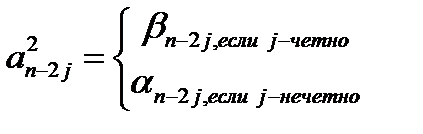
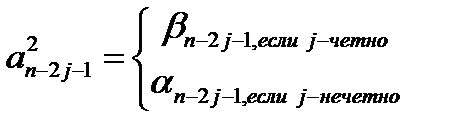
Коэффициенты 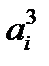многочлена 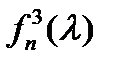имеют вид:

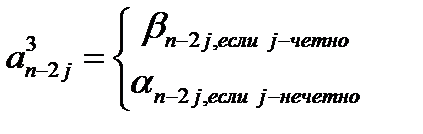
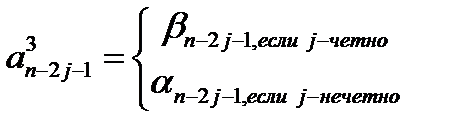
Коэффициенты 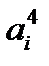многочлена 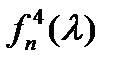таковы:

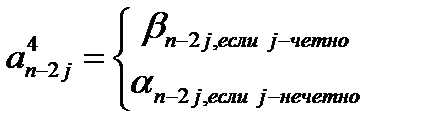
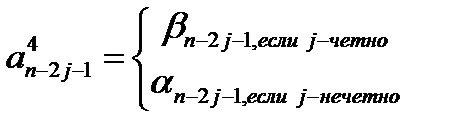
Теорема 5 (B. Л. Харитонов). Для того чтобы любой многочлен 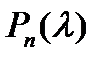вида (14) с коэффициентами; удовлетворяющими условиям (15), был устойчивым, необходимо и достаточно, чтобы все четыре многочлена 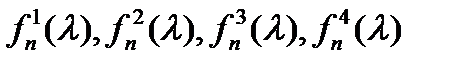были устойчивыми.

Пример 1. Установим необходимые и достаточные условия асимптотической устойчивости множества скалярных систем третьего порядка

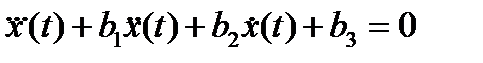(16)

с коэффициентами, удовлетворяющими условиям

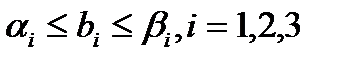(17)

Характеристический многочлен уравнения (16) имеет вид

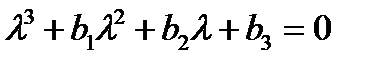
Построим многочлены :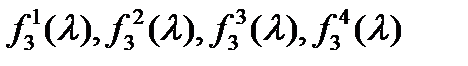

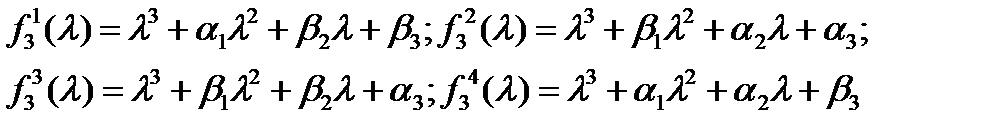(18)

Запишем условия устойчивости многочленов (18). Они имеют вид

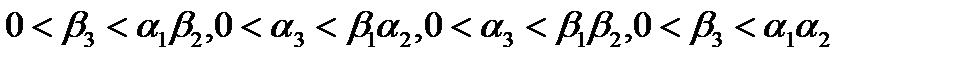(19)

Поскольку 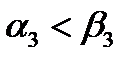и 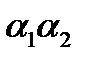меньше любого из произведени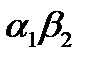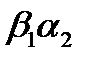й , и 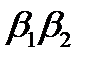, все условия (19) будут выполняться одновременно, если окажется выполненным лишь одно неравенство

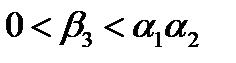(20)

Таким образом, все уравнения из множества (16) с коэффициентами, удовлетворяющими условию (17), устойчивы, если выполнены неравенства (20). Эти неравенства представляются весьма естественными. Если же они нарушаются, то, взяв уравнение (16), у которого 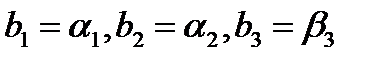, получим неустойчивое уравнение.